Tree (abstract data type)

A simple example unordered tree

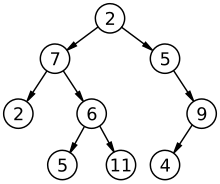
In computer science, a tree is a widely-used data structure that emulates a tree structure with a set of linked nodes. It is an acyclic and connected graph. Most of the literatures also include the constraint that a graph's edges must be undirected to be a tree. In addition to these three constraints, some literature indicates that a graph's edges should be un-weighted to be a tree.

Terminology

A node may contain a value or a condition or represent a separate data structure or a tree of its own. Each node in a tree has zero or more child nodes, which are below it in the tree (by convention, trees grow down, not up as they do in nature). A node that has a child is called the child's parent node (or ancestor node, or superior). A node has at most one parent.

The height of a node is the length of the longest downward path to a leaf from that node. The height of the root is the height of the tree. The depth of a node is the length of the path to its root (i.e., its root path). This is commonly needed in the manipulation of the various self balancing trees, AVL Trees in particular. Conventionally, the value -1 corresponds to a subtree with no nodes, whereas zero corresponds to a subtree with one node.

The topmost node in a tree is called the root node. Being the topmost node, the root node will not have parents. It is the node at which operations on the tree commonly begin (although some algorithms begin with the leaf nodes and work up ending at the root). All other nodes can be reached from it by following edges or links. (In the formal definition, each such path is also unique). In diagrams, it is typically drawn at the top. In some trees, such as heaps, the root node has special properties. Every node in a tree can be seen as the root node of the subtree rooted at that node.

Nodes at the bottommost level of the tree are called leaf nodes. Since they are at the bottommost level, they do not have any children. A node with no children is called a leaf node. They are also referred to as terminal node.

An internal node or inner node is any node of a tree that has child nodes and is thus not a leaf node. An intermediate node between the root and the leaf nodes is called an internal node.

A subtree is a portion of a tree data structure that can be viewed as a complete tree in itself. Any node in a tree T, together with all the nodes below it, comprise a subtree of T. The subtree corresponding to the root node is the entire tree; the subtree corresponding to any other node is called a proper subtree (in analogy to the term proper subset).

Tree ordering

There are two basic types of trees. In a recursive tree or unordered tree, a tree is a tree in a purely structural sense — that is to say, given a node, there is no order for the children of that node. A tree on which an order is imposed — for example, by assigning different natural numbers to each edge leading to a node's children — is called an edge-labeled tree or an ordered tree with data structures built upon them being called ordered tree data structures.

Ordered trees are by far the most common form of tree data structure. Binary search trees are one kind of ordered tree.

Tree representations

There are many different ways to represent trees; common representations represent the nodes as records allocated on the heap (not to be confused with the heap data structure) with pointers to their children, their parents, or both, or as items in an array, with relationships between them determined by their positions in the array (e.g., binary heap).

Trees as graphs

In graph theory, a tree is a connected acyclic graph. A rooted tree is such a graph with a vertex singled out as the root. In this case, any two vertices connected by an edge inherit a parent-child relationship. An acyclic graph with multiple connected components or a set of rooted trees is sometimes called a forest.

Traversal methods

Main article: Tree traversal

Stepping through the items of a tree, by means of the connections between parents and children, is called walking the tree, and the action is a walk of the tree. Often, an operation might be performed when a pointer arrives at a particular node. A walk in which each parent node is traversed before its children is called a pre-order walk; a walk in which the children are traversed before their respective parents are traversed is called a post-order walk.

Common operations

• Enumerating all the items
• Enumerating a section of a tree
• Searching for an item
• Adding a new item at a certain position on the tree
• Deleting an item
• Removing a whole section of a tree (called pruning)
• Adding a whole section to a tree (called grafting)
• Finding the root for any node

Common uses

• Manipulate hierarchical data
• Make information easy to search (see tree traversal)
• Manipulate sorted lists of data
• As a workflow for compositing digital images for visual effects

See also

• Binary space partitioning
• Heap
• Tree (graph theory)
• Tree (set theory)
• Tree structure
• Trie
• Exponential tree

Popular tree data structures

• Binary Tree

Self balancing binary search trees

Self-balancing binary search trees:

• AA tree
• AVL tree
• Red-black tree
• Splay tree
• Scapegoat tree

Other trees

• B-tree (2-3 tree, B+ tree, B*-tree, UB-tree)
• DSW algorithm
• Dancing tree
• Enfilade
• Fusion tree
• kd-tree
• Octree
• Quadtree
• R-tree
• Radix tree
• Segment tree
• Skip list
• T-tree
• T-pyramid
• Top Trees
• Van Emde Boas tree

References

• Donald Knuth. The Art of Computer Programming: Fundamental Algorithms, Third Edition. Addison-Wesley, 1997. ISBN 0-201-89683-4 . Section 2.3: Trees, pp.308–423.
• Thomas H. Cormen, Charles E. Leiserson, Ronald L. Rivest, and Clifford Stein. Introduction to Algorithms, Second Edition. MIT Press and McGraw-Hill, 2001. ISBN 0-262-03293-7 . Section 10.4: Representing rooted trees, pp.214–217. Chapters 12–14 (Binary Search Trees, Red-Black Trees, Augmenting Data Structures), pp.253–320.

External links

• Description from the Dictionary of Algorithms and Data Structures
• STL-like C++ tree class
• Description of tree data structures from ideainfo.8m.com
• flash actionscript 3 opensource implementation of tree and binary tree — opensource library