Talk:Monty Hall problem: Difference between revisions
Rick Block (talk | contribs) →A concrete proposal: new section |
|||
| Line 419: | Line 419: | ||
===Comments on the above proposal=== |
===Comments on the above proposal=== |
||
I think Nijdam said it best. "In the light of the ongoing discussion this seemes highly premature, not to say complete without any sense of reality." [[User:Glkanter|Glkanter]] ([[User talk:Glkanter|talk]]) 17:34, 29 March 2009 (UTC) |
|||
Revision as of 17:34, 29 March 2009
| This is the talk page for discussing changes to the Monty Hall problem article itself. Please place discussions on the underlying mathematical issues on the Arguments page. If you just have a question, try Wikipedia:Reference desk/Mathematics instead. |
| This article is of interest to the following WikiProjects: | ||||||||||||||
| ||||||||||||||
 | Monty Hall problem is a featured article; it (or a previous version of it) has been identified as one of the best articles produced by the Wikipedia community. Even so, if you can update or improve it, please do so. | |||||||||||||||||||||
| This article appeared on Wikipedia's Main Page as Today's featured article on July 23, 2005. | ||||||||||||||||||||||
| ||||||||||||||||||||||
New archive
This page has been quiet for a few weeks, so I created a new archive at Talk:Monty Hall problem/Archive 9 for the discussions from mid Oct 2008 through Feb 2009 (indicated as "archived" above). Several of the issues aren't exactly resolved (they will perhaps never be resolved to everyone's satisfaction), but the period of relative calm seemed like an opportune time to create a new archive. I added a new section (post archiving) much like this one. user:Glkanter has reverted these changes, suggesting we talk about it first. OK. Since we're at a lull in the discussion here, and the talk page is huge, I suggest now is an appropriate time to archive. -- Rick Block (talk) 15:14, 15 March 2009 (UTC)
- Agree with archiving now. The talk page is monster-sized, and nobody is going to read through it all anyway. –Henning Makholm (talk) 15:29, 15 March 2009 (UTC)
- I don't agree there has been a 'lull'. It's just been re-directed to the arguments page. I assume most readers (not necessarily editors) do NOT read archives. If they're interested, maybe they get as far as a talk page. Anyway, I think that the existence and vehement nature of the MHP article disagreement would not be evident if the entire thing were archived. A reader might think that there was universal satisfaction with the construction of the article. That would be an inaccurate impression to give. Glkanter (talk) 15:55, 15 March 2009 (UTC)
- This thread will remain here, and it already says there are unresolved issues. If you'd like to enumerate them here that will remain here as well. Good enough? -- Rick Block (talk) 17:37, 15 March 2009 (UTC)
- I didn't know there was an "arguments" page, so I too thought it had settled down. It would be very useful to have a concise list here of what the ongoing issues about the article are, phrased as neutrally as possible, with links to where some discussion about them may be found. Dicklyon (talk) 21:38, 15 March 2009 (UTC)
- The main one continues to be around whether it's necessary for the problem to be approached as a problem in conditional probabilities (i.e. whether an "unconditional solution" is sufficient). I wrote a FAQ section on this (referenced from the top of this page, see Talk:Monty_Hall_problem/FAQ). -- Rick Block (talk) 21:53, 15 March 2009 (UTC)
- The issue is there's a faction here (Glkanter and Martin Hogbin, perhaps others) who think the conditional analysis is completely unnecessary and that the problem as generally stated is appropriately addressed by an unconditional solution. They strongly object to Morgan et al.'s characterization of unconditional solutions as "false" solutions. There are others (Nijdam, for one, and I believe most participants in WP:WikiProject Mathematics willing to comment) who object to presenting an unconditional solution as the solution, since (in their view) an unconditional solution isn't actually addressing the problem as stated (and think whether or not the problem is stated to force a 2/3 answer, the unconditional solution is basically wrong). I've been suggesting the folks in favor of presenting an unconditional solution offer up a reference for such a solution from a source that understands the difference between conditional and unconditional. So far, no source has been offered. Most popular sources (notably vos Savant) ignore this issue - one is tempted to conclude most popular sources do not understand it. -- Rick Block (talk) 22:47, 15 March 2009 (UTC)
- So, lacking such other sources, we should obviously present the "usual" unconditional solution, with sources, and also the "conditional" solution and the fact of who says it's necessary and that the other is inadequate. Or does someone argue for more than this, or less than this? Dicklyon (talk) 23:28, 15 March 2009 (UTC)
- The specific problem with the current article is that it offers a somewhat wordy unconditional solution as the first solution. But then immediately follows that by saying "Although the reasoning above is correct it doesn't answer the precise question posed by the problem,...". Then the lengthy remainder of the article addresses this so-called deficiency. So, if I'm trying to settle a bet (of course using the unconditional solution, just try using the other stuff in a bar), the other guy says to me, 'but Wikipedia says that's not the solution'. So, as long as any claims that the unconditional solution is inadequate remain in the article, I am not for a two-tier solution. Glkanter (talk) 03:29, 16 March 2009 (UTC)
- But aren't the "claims that the unconditional solution is inadequate" well sourced? Or are you suggesting that Morgan et al. 1991 should be treated as just an opinion? And are you saying that the "one tier" or unconditional solution is adequate? Based on a source that says so? Or based on the fact that it comes up with the same answer, in terms of player strategy and average probability of winning, even though it's not an air-tight proof? Or based on the "standard analysis" where the host must "open one of the remaining two doors randomly if the player initially picked the car (Barbeau 2000:87)"? In this "standard" interpretation, is the idea that the host's action offers no new information about the probability of the originally chosen door have a car, and therefore it's a non-event and you don't need a conditional analysis? Or what? Could we resolve this by having a section the "standard interpretation" and its standard simple solution, and another section on other interpretations that require the more elaborate analysis? Dicklyon (talk) 04:32, 16 March 2009 (UTC)
- As you know, I reject the argument that the unconditional solution is inadequate. Interestingly, you bring up the point that Monty's decision only happens when the contestant chooses the car. Rick mentioned the same thing tonight. I just can't get past the idea that Monty choosing between two losing doors has any affect on the probability of winning. Check out the last section of the Arguments page for the latest and greatest unconditional solution. It contains no goats and no Monty. And, it has been approved as an unconditional solution to the MHP by a Wikipedia guru.
- http://en.wikipedia.org/wiki/User_talk:Tsirel#Is_this_a_valid_unconditional_proof_of_the_Monty_Hall_Problem.3F It's the 3rd section from the bottom. Glkanter (talk) 05:43, 16 March 2009 (UTC)
- Well, I think we can all agree that "Monty choosing between two losing doors" doesn't have any affect on the probability of winning, normally; but your "proof" is just an assertion with no proof logic, so hardly helpful at convincing anyone that it can be made rigorous. If you add some condition, like that Monty reveals no extra information about the prob of the first door having a car behind it, then it could be made rigorous pretty easily. On the other hand, if you allow Monty to reveal extra info, either by being known to always choose the left-most goat, or by stopping to flip a coin when the contestant has chosen a car, then you've got a different problem, requiring a different solution (in this latter case, the contestant's probability of winning a car is 100% if he follows the optimal strategy of switching only if Monty doesn't flip a coin). Dicklyon (talk) 05:52, 16 March 2009 (UTC)
- If you agree that ""Monty choosing between two losing doors" doesn't have any affect on the probability of winning, normally;..." then we're done here. Maybe I don't speak such good probability, but I'm sure you agree that 1/3 of the time the contestant picks the car. And that the probability of 'car' or 'not car' = 1. And that 1 - 1/3 = 2/3. And you just agreed that ""Monty choosing between two losing doors" doesn't have any affect on the probability of winning, normally;...". What's the problem? Why is this unconditional solution inadequate? Please note, the solution makes no mention of a 'Monty' or any 'goats'. What do you make of the comment at the above link? And I agree, the contestant knowing of a left door Monty bias, or flipping a coin is a new constraint to a different problem than the MHP. Glkanter (talk) 06:22, 16 March 2009 (UTC)
- There's a problem here, which is that the "proof" is not showing what it purports to show. What it does show is that if the player decides to switch before the host opens a door she has a 2/3 chance of winning. However, the question is what is the chance of winning when deciding to switch after the host opens a door. The problem can be (but often isn't) sufficiently constrained to make these the same. The whole point of the Morgan et al. paper (and the Gillman paper, and this point is echoed in the Grinstead and Snell book and others) is that an unconditional approach is fundamentally the wrong way to approach this kind of problem and using one without qualification is unsound at best (Morgan considers these "false" solutions). My understanding is that Glkanter does not agree with this, and does not want anything like it in the article - no matter how many reliable sources say it. The bottom line is that Morgan et al., and Gillman, and others basically discredit the unconditional approach which means (to me) that Wikipedia should either not present an unconditional "solution" at all, or is obligated to follow it up with the very sorts of words Glkanter objects to. -- Rick Block (talk) 14:45, 16 March 2009 (UTC)
- I sort of agree; not because the "proof is not showing what it purports to show", but because we have reliable sources that say so. The simple proof can even be made "correct", based on those same sources I suspect, by showing that the "chance of winning when deciding to switch after the host opens a door" can not change from the "chance of winning when deciding to switch before the host opens a door" under some reasonable and normal set of assumptions. They can both be correct, and both rigorous, if the problem is appropriately formulated. Dicklyon (talk) 16:16, 16 March 2009 (UTC)
- The value of the unconditional solution is that it explains the underlying logic (why 2/3 instead of 1/2) in a nice, simple way. If it were offered as an entirely valid analysis of the basic veridical paradox, then followed up with a "however, the problem as stated requires a more complicated solution", we'd have a good article. We're not willing to do this: instead, we say "here's the unconditional solution, which is wrong". We need to say, with no neurosis, "the unconditional solution is right, albeit in a constrained manner". And furthermore we need to focus on offering the unconditional solution in the clearest possible way in order to make the article as useful as possible to the general reader: right now, it's statisticiancruft.
- Unfortunately, the "problem as stated" has the attention of this article's editors to a degree that harms our ability to offer a solid, simple explanation to our readers. During the time that I've been involved with this article, I've seen it constantly degrade in quality. There's a pedantry at work that forces every explanation of the unconditional solution we offer to mutate into something that straddles the unconditional and conditional solutions, compromising both accuracy and clarity. We've got to ditch this neurosis and be willing to offer both solutions robustly, while noting the limitations of each.
- Drop the textbooks for a second and think about how you would write this article to be useful to an audience of 10-year-olds. Then write that article, and add to it whatever is needed to make it useful to a statistician as well.--Father Goose (talk) 16:47, 16 March 2009 (UTC)
- What would the "solid, simple explanation" be an explanation of? If an explanation of the "problem as stated," then the editors' attention is correctly directed. If it is an explanation of something else, what is it? The problem as usually understood? Please clarify. Visualaudio (talk) 04:21, 28 March 2009 (UTC)
I agree with a lot that Father Goose said, but not 100%. I refuse to focus on anything but the original 1/3 car and 2/3 not car. And nobody has ever said how the 1/3 can possibly change, so the 2/3 can't change either. There's an old saying, 'Are you interested, or committed? The hen, who provided the eggs, is interested in your breakfast, the pig, who provided the bacon, is committed to your breakfast.' I'm committed to the unconditional solution as being valid, rigorous, complete, etc. My goal all along has been to eliminate any statements in the Article, let alone the Solutions section, that undercuts this. The heck with the 10 year old. Try getting paid off on a bet by explaining the 'equal goat door constraint'. Glkanter (talk) 19:51, 16 March 2009 (UTC)
- I more or less agree with that. That's not to say that we need to drop the conditional explanations, the Bayesian analysis, or anything else. It's just that we need to have an absolutely pristine explanation of the unconditional analysis (such as the one diagrammed here) that is wholly untouched by conditional gremlins.
- The fact that every unconditional explanation present in the article keeps getting butchered into a conditional explanation (or worse still, a pseudo-conditional one) is a source of anguish to me. I'm serious, it anguishes me. It results in us having an article that is of negative value to the overwhelming majority of our readers, as it fails to give them a nice, simple, accurate, easy-to-understand solution to the paradox in its most general form, and misleads them into thinking that that solution is for some reason an invalid way to analyze the paradox -- which it is not. It's an invalid way to analyze the question-as-usually-asked -- but the question-as-usually-asked is not the subject of the article -- the paradox is. The question-as-usually-asked is merely one of the "sources of confusion", which has led our explanation of the paradox to be a confused one as well.--Father Goose (talk) 22:06, 16 March 2009 (UTC)
- Rick, would you be willing to consider a rewrite, with my help if need be, that would allow both the "conditional" and "unconditional" explanations to be fully and clearly presented, without introducing any inaccuracies?--Father Goose (talk) 22:10, 16 March 2009 (UTC)
- Propose away. I think this version has the exact structure you're suggesting. I'll also note that even the current version doesn't say the unconditional solution is wrong, just that it doesn't answer the precise question that is asked (which is what the reliable sources actually say). I'd suggest anyone consider rewording the solution consider whether the wording holds for slight variants - like the "host forgets" variant (where the correct answer is probability of winning by switching is 1/2, not 2/3) or the "host opens leftmost door if possible" variant (where the correct answer is probability of winning by switching is 1/2 or 100% depending on which door the host opens). The point of thinking about such variants is to explore how "robust" the solution is. If your solution only works for one carefully constructed version of the problem, it probably doesn't explain anything at all about the underlying logic. -- Rick Block (talk) 01:43, 17 March 2009 (UTC)
- That version still contaminates the simple solution section with the statement "Although the reasoning above is correct it doesn't answer the precise question posed by the problem, which is whether a player should switch after being shown a particular open door." It might be better to present a problem that this is the exactly correct solution to, and then treat the other problem where's it's not separately. A simple way to do this is to introduce the condition that the host choose randomly when there are two goats left, in a way that reveals no additional information to the contestant (since, as I pointed out, if he chooses random by flipping a coin only when he has to, and the contestant can see that, then it's a completely different ball game), so that the contestant's strategy of always switching is clearly going to lead to 2/3 chance of winning, without any conditionalizing on which door the host opens. In the diagram that Father Goose linked, I think one can rigorously show that "The player has an equal chance of initially selecting the car, Goat A, or Goat B. Switching results in a win 2/3 of the time." as it says in the caption, and that no strategy of maybe not switching based on which door the host opens can beat that. Dicklyon (talk) 02:25, 17 March 2009 (UTC)
- Contaminates? That wording is sourced - the exact quote is "F1's [one unconditional solution's] beauty as a false solution is that is is a true statement! It just does not solve the problem at hand". If someone can come up with a reference for a version of the MHP for which this solution (or any unconditional solution) is the exactly correct solution that'd be great - although one of the points of the Morgan et al. and Gillman papers is that the problem is about conditional probabilities (so I'm kind of skeptical that anyone is going to find such a reference). Per the question I've added to Talk:Monty Hall problem/FAQ, Gillman suggests an unconditional solution would be appropriate for a version where "you need to announce before a door has been opened whether you plan to switch" (which is such an unusual wording I don't think anyone would claim it's still the MHP). Ultimately the only thing that matters here is references. Change the article to say anything you'd like. But base it on references, not WP:OR. -- Rick Block (talk) 04:08, 17 March 2009 (UTC)
- Yes, "contaminates" in the sense of the proposal above for a discussion that is "wholly untouched by conditional gremlins." We all agree that there are sources that say such an analysis in inadequate; but it would not be NPOV to rely only on that analaysis. Try this one: [1]. Do we have to all agree that it's mathematically "exactly correct" in order to report what it says? It does look pretty carefully done, as it lists a bunch of assumptions needed to conclude that the host's opening of a door "gives no additional information about the likhihood of the initially chosen door being correct. etc." Dicklyon (talk) 04:17, 17 March 2009 (UTC)
- "Do we all have to agree it's mathematically exactly correct"? No, however given that this is a featured article we should clearly do our best to use sources of the highest quality, particularly if we're talking about a source for what will be presented as the "main" solution (which is what I believe some folks are talking about here). This source says the probability of winning by switching is .67 - which (IMO) makes this source somewhat suspect (and if the point is to use this as a "gold standard" for the solution, I would say we can't interpret this "loosely" as 2/3). It's also published as an appendix to vos Savant's book, and listed on the copyright page of the book as a reprint - which brings up the question of where it was originally published. As best as I can tell this appendix is a revised version (not a reprint) of this paper originally published in Personality and Social Psychology Bulletin (I did a lot of the original sourcing for this article, so I have most of the sources - including vos Savant's book and this paper). Note that this is a psychology journal, not a math journal, which makes this an excellent source for psychological aspects of the Monty Hall problem, but a somewhat less excellent source for mathematical aspects (and, I'll note, Granberg is a professor of sociology at the University of Missouri, not a mathematician). Does this mean we can't use this source? No. In fact, it's already referenced in the article (both the original paper and the "reprint" from vos Savant's book). On the other hand, I would hesitate to use this paper as the source for what we intend to be a mathematically sound unconditional solution. -- Rick Block (talk) 14:09, 17 March 2009 (UTC)
- Let me ask you, Rick: does this diagram somehow not map perfectly onto a truly unconditional presentation of the problem? If not, could tweaks be made to it to make it a truly unconditional framing of the problem?--Father Goose (talk) 05:55, 17 March 2009 (UTC)
- The diagram has the same basic issue as vos Savant's solution published in the December 1990 Parade column, which is that the problem says to consider the case where the player has picked door 1 and the host has opened door 3 (using these as representative of the situation where the player is deciding to switch after picking one of the doors and the host has opened another one) but the solution considers other cases. In the diagram the player has picked door 1 only in case 1 (so cases 2 and 3 simply don't apply - at least not to the problem as stated) and the host opens door 2 sometimes in case 1 and all the time in case 3 (so even case 1 doesn't always apply and again case 3 never applies). We could presumably restate the problem somehow to make the diagram fit (putting us in WP:OR territory), perhaps:
- You'll pick one of these three doors and after you've made your choice I'll open a different door revealing a goat. You can choose now whether your "final" door will be your original pick or the other door that remains unopened after I've opened a door to show a goat. Now, what door would you like and would you like it to be your final door or would you prefer to switch to the other door that's left after I open a door?
- Let me ask you something: doesn't the diagram currently in the article clearly show the exact problem that's asked? The player's pick is always door 1 (but the car can be behind any door), and the two cases (host opens door 2 vs. host opens door 3) are clearly grouped. In the problem as asked, the host opens door 3 putting us in the right half of the picture where switching wins twice as often as staying. -- Rick Block (talk) 14:09, 17 March 2009 (UTC)
- The diagram has the same basic issue as vos Savant's solution published in the December 1990 Parade column, which is that the problem says to consider the case where the player has picked door 1 and the host has opened door 3 (using these as representative of the situation where the player is deciding to switch after picking one of the doors and the host has opened another one) but the solution considers other cases. In the diagram the player has picked door 1 only in case 1 (so cases 2 and 3 simply don't apply - at least not to the problem as stated) and the host opens door 2 sometimes in case 1 and all the time in case 3 (so even case 1 doesn't always apply and again case 3 never applies). We could presumably restate the problem somehow to make the diagram fit (putting us in WP:OR territory), perhaps:
- Let me ask you, Rick: does this diagram somehow not map perfectly onto a truly unconditional presentation of the problem? If not, could tweaks be made to it to make it a truly unconditional framing of the problem?--Father Goose (talk) 05:55, 17 March 2009 (UTC)
- Accept for a second that the unconditional diagram is not a depiction of the conditionally stated problem. Pretend for a second that you've never heard of the Parade version of the problem (or any other conditionally phrased version), and that you're trying to create a diagram that depicts a purely unconditional form of the problem. Does this diagram successfully do that? If not, what changes would be needed to make it represent an unconditional form of the problem?--Father Goose (talk) 21:10, 18 March 2009 (UTC)
Rick, checking back, I see you're been shepherding this article for many years, since before it made "featured" in 2005. But at that time, it didn't have any of the current problem, of overloading the commonly-published simple solution with all the conditional stuff, and all the strife, confusion, and bloat that has come from that. A solution to the problem was proposed above. Surely you have enough good sources, including the Granberg paper with its list of conditions to make the initial 1/3 probability not change when a goat is revealed, to fix the problem as suggested. If you don't want to use this source on its own, because some idiot editor converted 2/3 to .67, combine it with some others that don't make that mistake. But don't us this stuff about him not being a mathematician; it doesn't take a professional mathematician to analyze a problem in probability, does it? Dicklyon (talk) 15:14, 17 March 2009 (UTC)
- Yes, I originally nominated it as a featured article and responded to the criticisms from the FAC review, and the two FARs it's been through as well. My opinion is almost exactly the opposite of Father Goose's - specifically that it has dramatically improved over the last several years (it was originally woefully under-referenced and presented a very shaky unconditional argument as its main "solution"). The inclusion of a more mathematically rigorous solution was largely due to the efforts of an anonymous editor, shortly before the most recent FAR with highly voluminous discussions on the talk page (starting at Talk:Monty Hall problem/Archive 6#Rigorous solution). This editor was the first to mention the Morgan et al. reference - which I believe is the first mathematically rigorous treatment of the MHP published in a peer reviewed math journal. Since this rigorous treatment has already been published, there in all likelihood will never be another (Gillman is sort of an oddity - my assumption is Gillman's paper was already "in press" when the Morgan et al. paper actually appeared). There is certainly no shortage of popular sources about this problem, but the Morgan et al. paper is (more or less) the definitive reference.
- You ask whether it takes a professional mathematician to analyze a problem in probability. Of course, in general, no. On the other hand, this problem generates massive amounts of controversy, IMO (well, actually backed up by lots of psychology sources like Granberg) because it deals with conditional probabilities which are not very well understood by most people - but it is a very simple problem on the surface which leads many people to think they understand it when they actually don't. This problem generates so much controversy that "serious mathematicians" at this point pretty much refuse to talk about it since they understand the rat-hole it becomes. The "many people" who think they understand it but actually don't includes lots of people who write about it as well as lots of academics (as evidenced by the large numbers of academics who wrote to vos Savant telling her she was wrong). The point is not that it would take a professional mathematician to produce a sound unconditional solution for this problem, but that it is harder than it seems and just because something happens to be published about this problem does not mean it is mathematically sound.
- I definitely understand the request being made here - for an easily understandable (which probably means unconditional), convincing, and (I'll add) mathematically sound solution. Unfortunately, I am not aware of a published solution that meets this criteria. -- Rick Block (talk) 19:40, 17 March 2009 (UTC)
- Well, it's great that they got you to come around to the "rigorous" conditional solution. But I think think the Granberg reference is plenty adequate for the "usual" solution, irrespective of whether you think it's "rigorous". And you probably have others that present the usual solution along with some words to the effect that it's applicable when the host's action doesn't provide any extra information about the probability of the originally chosen door having a car. Just go with it. Leaving it the way it is is too higher-math POV. Dicklyon (talk) 22:06, 17 March 2009 (UTC)
- Here is another in which it is at least stated that the contestant "learns nothing new" to justify the usual solution; in this type of solution, the different between deciding ahead of time to switch and deciding after a door is opened is moot, based on the assumptions, so the actions you condition on are irrelevant and can be ignored. Oh, and by the way, it's the overwhelmingly most common analysis, and nobody disputes that it gives the right answer (that you should switch) and the right probability of winning (2/3), even if one did decimalize it poorly. Dicklyon (talk) 22:12, 17 March 2009 (UTC)
- It (or some other unconditional solution) is certainly the most common analysis and nobody disputes the "you should switch" answer, but plenty of folks note the actual probability of winning by switching (without the "equal goat constraint") is not 2/3 but something in the interval [0.5, 1]. vos Savant has even written about the "host forgets" variant [2] and says:
- Back in 1990, everyone was convinced that it didn’t help to switch, whether the host opened a losing door on purpose or not. Assuming a knowledgeable host who would always open a losing door, that was incorrect. (A knowledgeable host who opened a winning door on purpose wouldn’t have much of a show, would he?!)
- It (or some other unconditional solution) is certainly the most common analysis and nobody disputes the "you should switch" answer, but plenty of folks note the actual probability of winning by switching (without the "equal goat constraint") is not 2/3 but something in the interval [0.5, 1]. vos Savant has even written about the "host forgets" variant [2] and says:
- Now everyone is convinced that it always helps to switch, regardless of what the host knows. But this is just as incorrect!
- Here's some of my own WP:OR - the reason "everyone" now says it always helps to switch is because many sources (like, ahem, vos Savant - whose own book ironically enough is titled "The Power of Logical Thinking") have presented an unconditional solution for the original problem as the (or at least "a") correct solution. Whether it's the standard version or the host forgets version or the host always picks the leftmost door version, it's always a conditional probability problem. Using an unconditional solution without understanding exactly what you're doing is dangerous, and (more of my own WP:OR) most people who present an unconditional solution don't really know what they're talking about.
- We've tried to straddle this line before (e.g. this version). I have no objection to this in principle, so long as we're very clear about when and why an unconditional solution is valid. I don't like "Solution" and "Conditional solution" as equal level headers, perhaps Solution with subheaders for "Popular solution" and "Conditional solution". This has been discussed before, with no one on either the "unconditional" or "conditional" side willing to accept a section heading that implied anything other than "this is the solution" (which is why both have been in the same "Solution" section). -- Rick Block (talk) 02:02, 18 March 2009 (UTC)
- We should just ignore anyone who comes here to promote the idea that there is only one Right way to argue for the solution, whatever his or her preferred way is. That premise is contrary to the idea of an encyclopedia, and contrary to how things are solved in mathematics in general.
- Also, I don't think your headings are good -- "popular solution" appears to imply that there is something wrong with the solution (which the hoi polloi cannot appreciate); "conditional solution" sounds as if the solution itself is only valid on certain conditions.
- I suggest we drop the assumption that the headings should be noun phrases that describe the solution. Let them refer to a key idea used in the argument instead. Perhaps "Anticipated choice" and "Conditional probabilities" would do. –Henning Makholm (talk) 12:52, 18 March 2009 (UTC)
Slow down, guys!
This talk page is moving too fast for anybody but the most zealous editors to follow the debate. I suspect this in itself makes it difficult for a good consensus to form. How about we
- Archive the old stuff already.
- Put everybody on a "two talkpage comments per day" restriction.
That would give more people than the two or three protagonists a fighting chance to contribute, at the possible expense of arriving at a conclusion a little slower. But remember, there is no deadline! –Henning Makholm (talk) 13:04, 18 March 2009 (UTC)
- I'll slow down; thanks for your willingness to participate. Dicklyon (talk) 22:22, 18 March 2009 (UTC)
General criticisms of the article
At this time I have two criticisms of the article. One is that the diagram in the "popular solution" section depicts the "conditional solution" and thus is in the wrong section. Another is that if the "unconditional solution" is an invalid way to analyze the problem in general, then the simulation approach, as described, is invalid as well.--Father Goose (talk) 22:04, 18 March 2009 (UTC)
- Right, why don't you go back to that older version that did a better job on the usual solution, and substitute its image and change words as needed? I was just checking to see if the basic structure got any objections first. And on the simulation approach, it might be good to mention the conditions under which the simulation addresses the problem, hopefully from sources about the simulations. Dicklyon (talk) 22:21, 18 March 2009 (UTC)
- I strongly object to reverting to the earlier image since the current image has several advantages. In particular, the current image makes the conditional solution accessible, it matches the problem as described (player picks door 1 and host opens door 3) and its formatting is carefully arranged to convey additional meaning (the column widths reflect the relative probabilities of the items in the column and the "host opens door 3" vs. "host open door 2" cases are adjacent). Showing both images would be possible, but they're so close that this would be redundant. -- Rick Block (talk) 00:42, 19 March 2009 (UTC)
- Rick, I thought you had agreed in principle to represent the usual simple solution simply, without reference to complication by the conditional appproach. That figure does that, but it sounds like that's why you object now. I think you also need to reconsider your interpretation of what the problem says. It doesn't really say the host opens door 3, it merely uses that as an illustrative example, where it says "say No. 3", or at least that's the way many of us read it. So why complicate this section by trying to get it to anticipate the more complex interpretation? Dicklyon (talk) 03:55, 20 March 2009 (UTC)
- We can present an unconditional solution that doesn't conflict with a conditional solution - choosing to do otherwise seems perverse. Goose's original diagram (which, BTW, the current one descends from) keeps the arrangement of car and goats constant and varies the door the player selects. The current version flips this (consistent with the problem statement) making the placement of the car the dominant variable, rather than the player's pick. Either way works just fine for an unconditional solution and either way is a simplification (there are actually 9 possibilities of car placement and player pick). We want to show a simplification with 3 possibilities to resonate with the 1/3 chance of picking the car. The current diagram doesn't require the goats to be distinguishable and even works with empty doors rather than goats as well.
- I agree the "say No. 3" language is meant as an illustrative example and make no claim that the only case to be considered is when the host opens door 3. If you're interpreting anything I've said to mean this you're not understanding what I'm saying. What I am saying is that the question pertains to the probabilities involved after a player has picked a door (any door, not just door 1) and the host has opened some other door (not just door 3). llustratively, we call these "door 1" and "door 3", but we could just as well call them "the door the player initially picked" and "the door the host opened". Whatever we call these doors, "my interpretation" (this is really the interpretation of Morgan et al., and Gillman, and Grinstead and Snell - and pretty much any mathematician who reads the problem) is that we're talking about a conditional probability (not the "average" across all players, but the probabilities for a player initially selecting some specific door when the host has opened some other specific door in response). If we analyze the specific case of "door 1/door 3", we can generalize the answer for "door i/door j". If this answer is the same for all i and j, it must also be the same as the unconditional solution (but not vice versa). -- Rick Block (talk) 04:55, 20 March 2009 (UTC)
- No, I get what you mean, but I think the way the example was presented in the problem statement was also strongly suggestive of the situation wherein things are symmetric enough that you don't need to care which door is opened or how they're numbered or whether there might be any door-number-dependent aspect at all intended. Let's see what kind of diagrams are used in publications on the popular solution; maybe that will help guide us. Dicklyon (talk) 05:05, 20 March 2009 (UTC)
- If I may ask, what is your response to the two criticisms I made?--Father Goose (talk) 02:18, 19 March 2009 (UTC)
- Although I agree the current split into Popular and Conditional sections is kind of a mess (I don't mean this in a derogatory kind of way, it's pretty clearly simply a work in progress) I think the existing diagram can serve both purposes. Specifically, all but the very last line apply to both the conditional and unconditional analysis - and, ignoring the last line, you have switching wins with probability 1/3+1/3 and switching loses with probability 1/6+1/6.
- The simulation section explicitly says "a switching strategy really does win two out of three times on the average" (emphasis added). We could certainly make this more clear, and probably should. The "Combining doors" section has a similar issue, and a similar disclaimer. A long, long time ago, the "Combining doors" section was part of the main "Solution" section (it is another commonly presented "popular" solution). How about illustrating the popular solution section with the figure from this section? (this is my second edit to the talk page today, so I guess I'm done until tomorrow - I agree a rate limit here might help control the volume, and I think the /Arguments page is helping as well) -- Rick Block (talk) 03:08, 19 March 2009 (UTC)
- I would just like to point out that there are at least 2 separate discussions taking place regarding this article. And I understand there is a 3rd page as well. If our goal is to reach consensus on editing the Article, I think we would benefit from all editors being in 1 discussion. Yes? Glkanter (talk) 15:12, 19 March 2009 (UTC)
- Links to them please? If you mean the Arguments page, you'll have to get more specific, as I can't find much there about how to evolve the article. I don't need the math tutorial, as I understand the conditional solution just fine, unlike some people who don't seem to get it. But it's not the solution that most sources present, and it's not neutral to treat it is the only acceptable solution. These math arguments aren't going to help us get to a better article, I think. Dicklyon (talk) 04:04, 20 March 2009 (UTC)
- I'm not sure, but I think Glkanter means here, and at /Arguments, and at /Analysis (a page user:Martin Hogbin has created with his own WP:OR analysis). -- Rick Block (talk) 04:55, 20 March 2009 (UTC)
Criticism and a new approach
My general criticism of the article is that it is much too long. A specific criticism of the article is that the Bayesian analysis is cumbersome and restrictive. Why should the quiz-master use equal probabilities for the two doors to open, when he has a choice? I like to see the problem as a game in which the quiz-team (including the quiz-master) has various possible deterministic strategies, and in general will use one of the possible deterministic strategies at random, according to some probability distribution. At the same time, the player has various possible deterministic strategies, and in general will use one of these strategies at random, according to some probability distribution. Here is a complete list:
Quiz-team's 6 possible deterministic (non-random) strategies:
Car behind door 1 and QM will open door 2 when player chooses door 1
Car behind door 1 and QM will open door 3 when player chooses door 1
Car behind door 2 and QM will open door 1 when player chooses door 2
Car behind door 2 and QM will open door 3 when player chooses door 2
Car behind door 3 and QM will open door 1 when player chooses door 3
Car behind door 3 and QM will open door 2 when player chooses door 3
The player's 12 possible deterministic strategies:
Choose door 1 and switch if QM opens 2, switch if QM opens 3
Choose door 1 and switch if QM opens 2, don't switch if QM opens 3
Choose door 1 and don't switch if QM opens 2, switch if QM opens 3
Choose door 1 and don't switch if QM opens 2, don't switch if QM opens 3
Choose door 2 and switch if QM opens 1, switch if QM opens 3
Choose door 2 and switch if QM opens 1, don't switch if QM opens 3
Choose door 2 and don't switch if QM opens 1, switch if QM opens 3
Choose door 2 and don't switch if QM opens 1, don't switch if QM opens 3
Choose door 3 and switch if QM opens 1, switch if QM opens 2
Choose door 3 and switch if QM opens 1, don't switch if QM opens 2
Choose door 3 and don't switch if QM opens 1, switch if QM opens 2
Choose door 3 and don't switch if QM opens 1, don't switch if QM opens 2
This is a zero-sum game and it has a saddle-point, or equilibrium, when we allow randomized strategies, ie each of the two sides chooses from their respective lists at random, according to two lists of probabilities. The quiz-team's minimax strategy is to choose between each of their 6 fixed strategies with equal probabilities. Ie the location of the car is uniform at random (equal probabilities 1/3), and the quizmaster makes his choice of door to open by a fair coin toss, if he has a choice. Then the player cannot win with probability greater than 2/3. The player's minimax strategy is to choose his door initially uniformly at random and then to always switch. Thus he puts equal probabilities 1/3 on the 3 deterministic strategies in which he always switches, and never uses the other 9. This way the player is guaranteed to win the car with probability 2/3, whatever strategy is used by the quiz-team. Whether or not he wins the car with probability 2/3 given his own initial choice, and if you like, also given the choice of the quiz-master, depends on the quiz-team's strategy. For some conditions it can be above 2/3, for others below; the only guarantee we have is that it averages out at exactly 2/3.
I feel that the Bayesian analysis section therefore gives misleading information. The conditional probability, given your initial and given the quiz-master's choice, that the car lies behind "the other" closed door, is only 2/3 when the quiz-master's and indeed the whole quiz-team's behaviour has been unreasonably limited. In order for the player to win 2/3 of the time it is sufficient that the player makes a true random choice of door, and thereafter always switches. Whether or not the player is going to win with conditional probability 2/3 given his initial choice (and also given the quiz-master's choice, if you like), depends on the quiz-team's strategy. Which, we suppose, the player doesn't know.
See http://www.math.leidenuniv.nl/~gill/threedoors.pdf
I shall try to get this paper into a peer-reviewed journal.
Gill110951 (talk) 22:14, 22 March 2009 (UTC)
- @Gill: With your analysis as a zero-sum game, you're addressing a different problem than the stated MHP. You are analyzing the problem as if the player leaves home and after closing his front door decides what to do in all possible circumstances. But the MHP puts the player on stage, whith a door chosen (that's why it says: say No. 1) and seeing a goat behind another door (say No. 3). 82.75.140.46 (talk) 17:10, 23 March 2009 (UTC)
- You're right, in a sense. But what difference does it make? The player might just as well imagine what he will do if does first choose door 1 and then is shown a goat behind door 3. He can imagine in advance all possibilities. Or: we can imagine that he imagines in advance, all possibilities. What the game-theoretic analysis makes explicit is that there is no way he gets any guarantee by choosing a non-random strategy (ie deciding in advance certainly to choose door 1, etc). There is only a unique conditional solution to the problem, if we restrict the actions of the quizmaster. What we also learn is that the only way the quizmaster can guarantee that the player doesn't win with a probability larger than 2/3 (unconditional) is to put the car behind a uniform random door, and to open a uniform random door when he has a choice. At the same time, the only way the player can guarantee himself to win with probability at least 2/3 is to choose his door uniform at random and thereafter always to switch doors. In the situation that the quizmaster plays the minimax strategy it is true that the conditional probability of the car being behind the other door is 2/3. But how do we know he uses the minimax strategy? I don't see it stated in the problem. So strictly speaking there is no answer to the question "what is the probability the car is behind the other door, given the player chose door 1 [even if he chose it uniformly at random] and the quizmaster opened door 3".
- By the way, I am not editing the page itself at this stage, just throwing a new titbit into the arena, for anyone who is interested. Since it is original new research - of the day before yesterday - I am not even allowed to put it on the page. Gill110951 (talk) 10:45, 24 March 2009 (UTC)
- Thanks you for your contribution, I think it confirms what I and other have been saying for some time which is that the Morgan paper, although not exactly wrong, answers a question than nobody would ever ask. Martin Hogbin (talk) 22:31, 26 March 2009 (UTC)
- In the fully explicit version stated in the article, which seems to match most people's expectations for how the problem should be defined, the host is constrained to open a door randomly if given a choice. This behavior is not specified in the Parade version, leaving open the possibility for other host behaviors. The Morgan et al. paper analyzes the Parade version and expresses this host behavior as a variable q (where q=1/2 means the host is constrained to pick randomly) and shows the player's chance of winning is 1/(1+q). With q=1/2 (which is not stated, but is perhaps the "intended" interpretation) the answer is 2/3, but since q can range from 0-1, the chance of winning by switching without this constraint varies between 1/2 and 1. Rather than confirming they've answered a question nobody would ever ask, I think this thread is confirming the exact opposite. -- Rick Block (talk) 00:12, 27 March 2009 (UTC)
- Rick, I think most people agree that Morgan et al.'s interpretation is a bit far fetched, and also it's still the case that averaged over the possible configurations the prob of winning by switching remains 2/3. Since there's nothing in the problem statement to suggest that door 3 was anything but an example, or that the answer could depend on what door the host opened, it takes a bit of imagination to formalate a problem in which it matters and in which the example given is taken to define the question being asked. Sure, it's a perfectly fine precise mathematical interpretation, with the added caveat that the host's choice can be modeled as a stochastic event, and Morgan et al. give a great solution of that problem. But reasonable balance and NPOV would suggest that we put the most weight on the mainstream interpretation of the problem. Right? Dicklyon (talk) 02:00, 27 March 2009 (UTC)
- I don't understand your point here. Are you saying the "mainstream interpretation" is that it's an unconditional problem? If the point of the problem is to evaluate the probabilities when the player is in front of two closed doors and one open door (which I think is the standard interpretation), then it's a conditional problem. The natural symmetry of the situation makes the conditional probability of interest the same as the unconditional probability, but without an explicit constraint that the host pick randomly if the player initially picks the car the problem is not necessarily symmetric. This is the main point of the Morgan et al. paper (and Gillman's paper, and numerous other references). It's a quite reasonable assumption that the host has no preference if the player's initial selection is the car and this makes the answer 2/3, but even explicitly stating this constraint doesn't turn it into an unconditional problem. Is there a competing POV here? -- Rick Block (talk) 04:52, 27 March 2009 (UTC)
- I'm not saying the mainstream interpretation is that it's an unconditional problem; rather, that in the mainstream interpretation that distinction doesn't come up, and so what you're calling the unconditional solution is generally considered to be the solution. Furthermore, the mainstream interpretation includes the symmetry condition when people go further and try to make it more mathematically rigorous by saying that the host's choices doesn't affect the 1/3 probability of the original choice still being the car after a door is opened. I quite understand the Morgan solution, and that he teaches that all other solutions are inadequate, but that's certainly not the mainstream view. Is it? Dicklyon (talk) 05:07, 27 March 2009 (UTC)
- It depends on what you mean by "mainstream interpretation". I believe the mainstream interpretation in published probability theory articles (Morgan et al., Gillman - there are more) and books (Grinstead and Snell for one) is that the problem is a conditional probability problem and that the host's choice when the player initially picks the car therefore matters. Likely because of Morgan et al. and Gillman, the "standard analysis" now includes the condition that the host pick randomly in this case - forcing the answer to unambiguously be 2/3 chance of winning by switching. On the other hand, the popular sources (starting with vos Savant) generally treat the problem as if the question were "what is the chance of winning if the player's predetermined strategy is to switch" (which is an unconditional problem). I don't think this is a POV issue - it's simply a case of the popular sources (led by vos Savant) choosing to answer a simpler question (without saying so - leaving the question open of whether they understand what they're talking about or not). Many of the solutions that claim the host's choice doesn't affect the player's initial 1/3 probability (because the host must open a door and must show a goat - without saying anything about the host's choice if the player initially picks the car) confuse unconditional and conditional probabilities and are arguably simply wrong (Falk is a good reference for this).
- Rather than continuing to argue about this, how about following an approach similar to the one used in Grinstead and Snell? They start with the sticker (wins 1/3) vs. switcher (wins 2/3) player strategy, but then go on to explain that this doesn't actually address the conditional probability question that the problem asks and show a conditional solution. -- Rick Block (talk) 00:03, 28 March 2009 (UTC)
- That's exactly what I'd like to see as well. We could, in the process, tie it closely to the "simulation" proof, since the usual form of the simulation is multiple trials of the unconditional problem. Using the unconditional problem to prove the solution (via a simulation) apparently had cachet with the originator of the problem (Gardner), so that's got to lend it some weight.--Father Goose (talk) 08:44, 28 March 2009 (UTC)
- Ok to me, be it that I would call the "simple solution" a "simple way of understanding" rather than a solution. And as Father Goose already mentioned, the simulation approach is mainly (always) the unconditional one, and the article should mention this shortcoming. Nijdam (talk) 10:07, 28 March 2009 (UTC)
- If you don't call it a "solution", you're inflicting a POV about what the problem is, which conflicts with the usual interpretation. And as the simulation, simulating an "always switch" strategy versus and "always stick" strategy doesn't really embody a conditional or unconditional probability model, does it? How is it a shortcoming? Dicklyon (talk) 14:51, 28 March 2009 (UTC)
- The usual simulation does not address the conditional probability the problem seemingly asks for. A proper simulation would keep track of switch/stay success per combination of initial player pick and door the host opens (6 combinations). Lumping these all together means the simulation answers the question "what is the chance of winning by switching if deciding to switch before the host opens a door". How about saying something like "Most popular sources assume that the question intends the probability of winning by switching to be the same whether the player decides to switch before or after the host opens a door, and analyze the before case." I believe this is the truth - but finding a reliable source that puts it this way might be challenging. -- Rick Block (talk) 16:20, 28 March 2009 (UTC)
- If you don't call it a "solution", you're inflicting a POV about what the problem is, which conflicts with the usual interpretation. And as the simulation, simulating an "always switch" strategy versus and "always stick" strategy doesn't really embody a conditional or unconditional probability model, does it? How is it a shortcoming? Dicklyon (talk) 14:51, 28 March 2009 (UTC)
- Ok to me, be it that I would call the "simple solution" a "simple way of understanding" rather than a solution. And as Father Goose already mentioned, the simulation approach is mainly (always) the unconditional one, and the article should mention this shortcoming. Nijdam (talk) 10:07, 28 March 2009 (UTC)
- That's exactly what I'd like to see as well. We could, in the process, tie it closely to the "simulation" proof, since the usual form of the simulation is multiple trials of the unconditional problem. Using the unconditional problem to prove the solution (via a simulation) apparently had cachet with the originator of the problem (Gardner), so that's got to lend it some weight.--Father Goose (talk) 08:44, 28 March 2009 (UTC)
- See, for example, /Arguments#Excel simulation of difference between "random goat" and "leftmost goat" variants. Note the effect the host strategy can have on the probability of winning by switching when given knowledge of which door the host opens. -- Rick Block (talk) 16:27, 28 March 2009 (UTC)
(outindent) Dick - you say "we get that". What "we" are you talking about? The question asks about a conditional probability (you agree with this don't you?). Without making it clear what they're doing, most popular sources present a solution based on an analysis of unconditional probabilities. For the conditional and unconditional probabilities to be the same, the host must pick randomly between two goats in the case the player initially picks the car. One might say the popular sources know what they're doing and are simply assuming this to be the case - others might say the popular sources are misunderstanding the problem and are, without realizing it, solving a different problem (one where the player must decide whether to switch before the host opens a door). Morgan et al. and Gillman (and many others) say the latter. You're saying it's POV for Wikipedia to say the popular sources are misunderstanding the problem (right?). Given the number of reliable sources that say exactly this, isn't it also POV to avoid saying it? I think this may perhaps be a case involving a prevalent popular misconception about something where the "experts" say the truth is something different than what is popularly believed to be true. Off hand, I can't think of other examples (surely there must be some). If anyone can think of others it might be interesting to see how they're handled. -- Rick Block (talk) 02:48, 29 March 2009 (UTC)
- By "we" I mean myself and any other intelligent discussants here; if someone doesn't get it by now, why bother talking to them? I understand what you're saying, especially that "Without making it clear what they're doing, most popular sources present a solution based on an analysis of unconditional probabilities." I don't think it's necessary to agree with you on "The question asks about a conditional probability (you agree with this don't you?)" since that's not the interpretation of most popular sources, as you note. As to whether the popular sources are "misunderstanding" or not, I don't think we have to know the answer to that. Morgan et al. and Gillman take a position on that, which we can report, but which we don't need to endorse. You can report as much as you like that top statisticians say the popular solution is wrong. But first you need to present the popular solution; then, move on to those who say it's wrong. Don't pollute the presentation of popular solution with the modern revised solution; first the one, then the other with an explanation of why they say the one is inadequate. That's the NPOV way to go about it. Dicklyon (talk) 03:01, 29 March 2009 (UTC)
(Counter)example
Maybe the next example is helpful to understand the problems with the problem.
I throw a fair dice. What is the probability of my outcome?
- Some people may reason: the outcome is one of the numbers 1 ... 6, so the probability that "the outcome is one of the numbers 1 ... 6" is 1. And they are right in some sense.
- The common meaning of the question is of course: for each possible outcome the probability is 1/6.
- Imagine you are standing next to me and you see the outcome of my throw. You definitely will say: 1/6.
Nijdam (talk) 09:29, 27 March 2009 (UTC)
- It's not clear what this is an example of. Dicklyon (talk) 15:45, 27 March 2009 (UTC)
- Please explain yourself instead. What is this an example of? How does it relate to the article? –Henning Makholm (talk) 17:00, 29 March 2009 (UTC)
Replace the Popular Solution Section With the 'Combining Doors' Solution
I propose the article be changed in the following way:
Replace the Popular Solution Section with the 'Combining Doors' Solution. Further, I would remove any statements regarding how the host chooses between the two doors. (Only 1 of the four sources in this section mention any 'host behaviour'). I would also add some formal notation of the diagrams, that would convey this:
Once the contestant has selected a door: 1/3 + (1/3 + 1/3) = 1 where the 1/3 on the left of the '+' sign represents the chosen door, and the numbers inside the parenthesis represent the remaining doors.
After a goat is revealed, the formula appears as: 1/3 + (2/3 + 0) = 1 or 1/3 +(0 + 2/3) = 1
As the only two possible outcomes are equivalent, regardless of which door the host reveals, this can be stated as: 1/3 + 2/3 = 1
Therefore switching, once it is offered by the host, will win the car 2x as often as not switching.
Glkanter (talk) 16:50, 27 March 2009 (UTC)
- In the light of the ongoing discussion this seemes highly premature, not to say complete without any sense of reality.Nijdam (talk) 17:25, 27 March 2009 (UTC)
A concrete proposal
Given the voluminous discussions above, and in the archives of this page and at the #Arguments page, how about the following? Please comment below. -- Rick Block (talk) 17:18, 29 March 2009 (UTC)
Solution
There are two main approaches to solving the Monty Hall problem that answer slightly different questions.
Is always switching better?
The probability of winning for all players who switch or all players who don't switch can be determined by examining all possible outcomes in either case (Grinstead and Snell 2006:137). For example, the figure below shows the outcomes when switching if the car is randomly placed behind one of the doors and the player initially picks Door 1. Switching will win if the car is behind either Door 2 or Door 3 with probability 2/3 while switching will lose only if the car is behind Door 1 with probability 1/3. Not switching wins if the car is behind Door 1 with probability 1/3, and otherwise loses with probability 2/3. The situation is similar no matter which door the player initially picks, so players who switch will win twice as often as players who don't.
Is switching always better?
The solution above shows that the probability of winning by switching for all players who switch is 2/3, but this does not necessarily mean the probability of winning by switching is 2/3 given which door the host opens. This probability is a conditional probability (Morgan et al. 1991; Gillman 1992; Grinstead and Snell 2006:137). The difference is whether the analysis, as above, considers all possible scenarios or only the scenarios where the host opens a specific door. Another way to express the difference is whether the player must decide to switch before the host opens a door or is allowed to decide after seeing which door the host opens (Gillman 1992). The conditional probability may differ from the overall probability depending on the exact formulation of the problem.
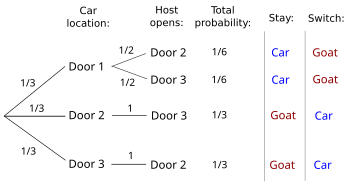
The conditional probability of winning by switching given which door the host opens can be determined referring to the expanded figure below or to an equivalent decision tree as shown to the right (Chun 1991; Grinstead and Snell 2006:137-138). For example, if the host opens Door 3 and the player switches, the player wins with overall probability 1/3 if the car is behind Door 2 and loses with overall probability 1/6 if the car is behind Door 1—the possibilities involving the host opening Door 2 do not apply. To convert these to conditional probabilities they are divided by their sum, so the conditional probability of winning by switching given the player picks Door 1 and the host opens Door 3 is (1/3)/(1/3 + 1/6), which is 2/3. This analysis depends on the constraint in the explicit problem statement that the host choose which door to open randomly if the player has initially selected the car.
Morgan et al. (1991) and Gillman (1992) both show a more general solution where the host is not constrained to pick randomly if the player has initially selected the car, which is how they both interpret the well known statement of the problem in Parade. They consider a scenario where the host chooses which door to open in this case with a preference expressed as a probability q, having a value between 0 and 1. If the host picks randomly q would be 1/2 and switching wins with probability 2/3 regardless of which door the host opens. If the player picks Door 1 and the host's preference for Door 3 is q, then in the case where the host opens Door 3 switching wins with overall probability 1/3 if the car is behind Door 2 and loses with overall probability (1/3)q if the car is behind Door 1. The conditional probability of winning by switching given the host opens Door 3 is therefore (1/3)/(1/3 + (1/3)q) which simplifies to 1/(1+q). Since q can vary between 0 and 1 this conditional probability can vary between 1/2 and 1. This means even without constraining the host to pick randomly if the player initially selects the car, the player is never worse off switching.
References
- Gillman, Leonard (1992). "The Car and the Goats," American Mathematical Monthly 99: 3–7.
- Grinstead, Charles M. and Snell, J. Laurie (2006-07-04). Grinstead and Snell’s Introduction to Probability (PDF). Online version of Introduction to Probability, 2nd edition, published by the American Mathematical Society, Copyright (C) 2003 Charles M. Grinstead and J. Laurie Snell. Retrieved 2008-04-02.
{{cite book}}: Check date values in:|date=(help)CS1 maint: multiple names: authors list (link) - Morgan, J. P., Chaganty, N. R., Dahiya, R. C., & Doviak, M. J. (1991). "Let's make a deal: The player's dilemma," American Statistician 45: 284-287.
Comments on the above proposal
I think Nijdam said it best. "In the light of the ongoing discussion this seemes highly premature, not to say complete without any sense of reality." Glkanter (talk) 17:34, 29 March 2009 (UTC)