Markov decision process: Difference between revisions
m robot Modifying: cs:Markovův rozhodovací proces |
|||
| Line 8: | Line 8: | ||
==Definition== |
==Definition== |
||
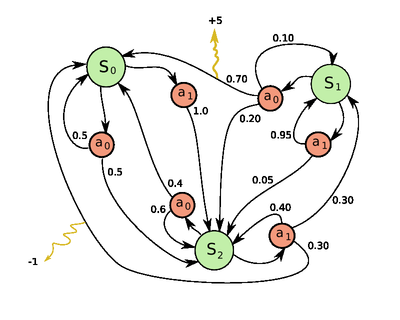
[[Image:Markov_Decision_Process_example.png|400px|right|thumb|Example of a simple MDP with 3 states and 2 actions.]] |
|||
A Markov decision process is a 4-[[tuple]] <math>(S,A,P_\cdot(\cdot,\cdot),R_\cdot(\cdot,\cdot))</math>, where |
A Markov decision process is a 4-[[tuple]] <math>(S,A,P_\cdot(\cdot,\cdot),R_\cdot(\cdot,\cdot))</math>, where |
||
Revision as of 20:48, 10 August 2010
Markov decision processes (MDPs), named after Andrey Markov, provide a mathematical framework for modeling decision-making in situations where outcomes are partly random and partly under the control of a decision maker. MDPs are useful for studying a wide range of optimization problems solved via dynamic programming and reinforcement learning. MDPs were known at least as early as the 1950s (cf. Bellman 1957). Much research in the area was spawned due to Ronald A. Howard's book, Dynamic Programming and Markov Processes, in 1960. Today they are used in a variety of areas, including robotics, automated control, economics and manufacturing.
More precisely, a Markov Decision Process is a discrete time stochastic control process. At each time step, the process is in some state , and the decision maker may choose any action that is available in state . The process responds at the next time step by randomly moving into a new state , and giving the decision maker a corresponding reward .
The probability that the process chooses as its new state is influenced by the chosen action. Specifically, it is given by the state transition function . Thus, the next state depends on the current state and the decision maker's action . But given and , it is conditionally independent of all previous states and actions; in other words, the state transitions of an MDP possess the Markov property.
Markov decision processes are an extension of Markov chains; the difference is the addition of actions (allowing choice) and rewards (giving motivation). Conversely, and ignoring rewards, if only one action exists for each state, a Markov decision process reduces to a Markov chain.
Definition
A Markov decision process is a 4-tuple , where
- is a finite set of states,
- is a finite set of actions (alternatively, is the finite set of actions available from state ),
- is the probability that action in state at time will lead to state at time ,
- is the immediate reward (or expected immediate reward) received after transition to state from state with transition probability .
(The theory of Markov decision processes does not actually require or to be finite,[citation needed] but the basic algorithms below assume that they are finite.)
Problem
The core problem of MDPs is to find a policy for the decision maker: a function that specifies the action that the decision maker will choose when in state . Note that once a Markov decision process is combined with a policy in this way, this fixes the action for each state and the resulting combination behaves like a Markov chain.
The goal is to choose a policy that will maximize some cumulative function of the random rewards, typically the expected discounted sum over a potentially infinite horizon:
- (where we choose )
where is the discount rate and satisfies . It is typically close to 1.
Because of the Markov property, the optimal policy for this particular problem can indeed be written as a function of only, as assumed above.
Solution
Suppose we know the state transition function and the reward function , and we wish to calculate the policy that maximizes the expected discounted reward.
The standard family of algorithms to calculate this optimal policy requires storage for two arrays indexed by state: value , which contains real values, and policy which contains actions. At the end of the algorithm, will contain the solution and will contain the discounted sum of the rewards to be earned (on average) by following that solution from state .
The algorithm has the following two kinds of steps, which are repeated in some order for all the states until no further changes take place. They are
Their order depends on the variant of the algorithm; one can also do them for all states at once or state by state, and more often to some states than others. As long as no state is permanently excluded from either of the steps, the algorithm will eventually arrive at the correct solution.
Notable variants
Value iteration
In value iteration (Bellman 1957), which is also called backward induction, the array is not used; instead, the value of is calculated whenever it is needed.
Substituting the calculation of into the calculation of gives the combined step:
This update rule is iterated for all states until it converges with the left-hand side equal to the right-hand side (which is the Bellman equation for this problem).
Policy iteration
In policy iteration (Howard 1960), step one is performed once, and then step two is repeated until it converges. Then step one is again performed once and so on.
Instead of repeating step two to convergence, it may be formulated and solved as a set of linear equations.
This variant has the advantage that there is a definite stopping condition: when the array does not change in the course of applying step 1 to all states, the algorithm is completed.
Modified policy iteration
In modified policy iteration (van Nunen, 1976; Puterman and Shin 1978), step one is performed once, and then step two is repeated several times. Then step one is again performed once and so on.
Prioritized sweeping
In this variant, the steps are preferentially applied to states which are in some way important - whether based on the algorithm (there were large changes in or around those states recently) or based on use (those states are near the starting state, or otherwise of interest to the person or program using the algorithm).
Extensions
Partial observability
The solution above assumes that the state is known when action is to be taken; otherwise cannot be calculated. When this assumption is not true, the problem is called a partially observable Markov decision process or POMDP.
Reinforcement Learning
If the probabilities or rewards are unknown, the problem is one of reinforcement learning (Sutton and Barto, 1998).
For this purpose it is useful to define a further function, which corresponds to taking the action and then continuing optimally (or according to whatever policy one currently has):
While this function is also unknown, experience during learning is based on pairs (together with the outcome ); that is, "I was in state and I tried doing and happened"). Thus, one has an array and uses experience to update it directly. This is known as Q-learning.
The power of reinforcement learning lies in its ability to solve the Markov decision process without computing the transition probabilities; note that transition probabilities are needed in value and policy iteration. Also, reinforcement learning can be combined with function approximation, and thereby one can solve problems with a very large number of states. Reinforcement Learning can also be handily performed within Monte Carlo simulators of systems.
Alternative notations
The terminology and notation for MDPs are not entirely settled. There are two main streams — one focuses on maximization problems from contexts like economics, using the terms action, reward, value and calling the discount factor or , while the other focuses on minimization problems from engineering and navigation, using the terms control, cost, cost-to-go and calling the discount factor . In addition, the notation for the transition probability varies.
| in this article | alternative | comment |
|---|---|---|
| action | control | |
| reward | cost | is the negative of |
| value | cost-to-go | is the negative of |
| policy | policy | |
| discounting factor | discounting factor | |
| transition probability | transition probability |
In addition, transition probability is sometimes written , or, rarely,
See also
- Partially observable Markov decision process
- Dynamic programming
- Bellman equation for applications to economics.
References
- R. Bellman. A Markovian Decision Process. Journal of Mathematics and Mechanics 6, 1957.
- R. E. Bellman. Dynamic Programming. Princeton University Press, Princeton, NJ, 1957. Dover paperback edition (2003), ISBN 0486428095.
- Ronald A. Howard Dynamic Programming and Markov Processes, The M.I.T. Press, 1960.
- D. Bertsekas. Dynamic Programming and Optimal Control. Volume 2, Athena, MA, 1995.
- M. L. Puterman. Markov Decision Processes. Wiley, 1994.
- H.C. Tijms. A First Course in Stochastic Models. Wiley, 2003.
- Sutton, R. S. and Barto A. G. Reinforcement Learning: An Introduction. The MIT Press, Cambridge, MA, 1998.
- J.A. E. E van Nunen. A set of successive approximation methods for discounted Markovian decision problems. Z. Operations Research, 20:203-208, 1976.
- S. P. Meyn, 2007. Control Techniques for Complex Networks, Cambridge University Press, 2007. ISBN 9780521884419. Appendix contains abridged Meyn & Tweedie.
- S. M. Ross. 1983. Introduction to stochastic dynamic programming. Academic press
External links
- MDP Toolbox for Matlab - An excellent tutorial and Matlab toolbox for working with MDPs.
- Reinforcement Learning An Introduction by Richard S. Sutton and Andrew G. Barto
- SPUDD A structured MDP solver for download by Jesse Hoey
- Learning to Solve Markovian Decision Processes by Satinder P. Singh







































