Linear network coding: Difference between revisions

Content deleted Content added

Inline

Revision as of 13:56, 4 February 2013

Linear network coding is a technique which can be used to improve a network's throughput, efficiency and scalability, as well as resilience to attacks and eavesdropping, as compared to traditional methods of OSI model or TCP/IP model separation between network layers with physical layer working on principles of Shannon Information Theory. Instead of simply relaying the packets of information they receive, the nodes of a network take several packets and combine them together for transmission. This can be used to attain the maximum possible information flow in a network.

It has been proven that linear coding is enough to achieve the upper bound in multicast problems.^[1] However linear coding is not sufficient in general (e.g. multisource, multisink with arbitrary demands), even for more general versions of linearity such as convolutional coding and filter-bank coding.^[2]

Encoding and decoding

In a linear network coding problem, a group of nodes $P$ are involved in moving the data from $S$ source nodes to $K$ sink nodes. Each node generates new packets which are linear combinations of earlier received packets, multiplying them by coefficients chosen from a finite field, typically of size $GF(2^{s})$ .

Each node, $p_{k}$ with indegree, $InDeg(p_{k})=S$ , generates a message $X_{k}$ from the linear combination of received messages $\{M_{i}\}_{i=1}^{S}$ by the relation:

X_{k}=\sum _{i=1}^{S}g_{k}^{i}\cdot M_{i}

where the values $g_{k}^{i}$ are the coefficients selected from $GF(2^{s})$ . Note that, since operations are computed in a finite field, the generated message is of the same length as the original messages. Each node forwards the computed value $X_{k}$ along with the coefficients, $g_{k}^{i}$ , used in the $k^{\text{th}}$ level, $g_{k}^{i}$ .

Sink nodes receive these network coded messages, and collect them in a matrix. The original messages can be recovered by performing Gaussian elimination on the matrix^{[citation needed]}. In reduced row echelon form, decoded packets correspond to the rows of the form $e_{i}=[0...010...0]$ .

A brief history

A network is represented by a directed graph ${\mathcal {G}}=(V,E,C)$ . $V$ is the set of nodes or vertices, $E$ is the set of directed links (or edges), and $C$ gives the capacity of each link of $E$ . Let $T(s,t)$ be the maximum possible throughput from node $s$ to node $t$ . By the max-flow min-cut theorem, $T(s,t)$ is upper bounded by the minimum capacity of all cuts, which is the sum of the capacities of the edges on a cut, between these two nodes.

Karl Menger proved that there is always a set of edge-disjoint paths achieving the upper bound in a unicast scenario, known as the max-flow min-cut theorem. Later, the Ford–Fulkerson algorithm was proposed to find such paths in a polynomial time. Then, Edmonds proved in the paper "Edge-Disjoint Branchings" the upper bound in the broadcast scenario is also achievable, and proposed a polynomial time algorithm.

However, the situation in the multicast scenario is more complicated, and in fact, such an upper bound can't be reached using traditional routing ideas. Ahlswede, et al. proved that it can be achieved if additional computing tasks (incoming packets are combined into one or several outgoing packets) can be done in the intermediate nodes.^[3]

The butterfly network example

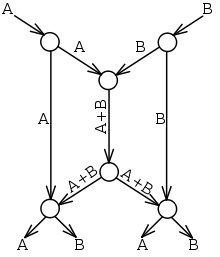
The butterfly network ^[3] is often used to illustrate how linear network coding can outperform routing. Two source nodes (at the top of the picture) have information A and B that must be transmitted to the two destination nodes (at the bottom), which each want to know both A and B. Each edge can carry only a single value (we can think of an edge transmitting a bit in each time slot).

If only routing were allowed, then the central link would be only able to carry A or B, but not both. Suppose we send A through the center; then the left destination would receive A twice and not know B at all. Sending B poses a similar problem for the right destination. We say that routing is insufficient because no routing scheme can transmit both A and B simultaneously to both destinations.

Using a simple code, as shown, A and B can be transmitted to both destinations simultaneously by sending the sum of the symbols through the center – in other words, we encode A and B using the formula "A+B". The left destination receives A and A + B, and can calculate B by subtracting the two values. Similarly, the right destination will receive B and A + B, and will also be able to determine both A and B.

Random network coding

Random network coding ^[4] is a simple yet powerful encoding scheme, which in broadcast transmission schemes allows close to optimal throughput using a decentralized algorithm. Nodes transmit random linear combinations of the packets they receive, with coefficients chosen from a Galois field. If the field size is sufficiently large, the probability that the receiver(s) will obtain linearly independent combinations (and therefore obtain innovative information) approaches 1. It should however be noted that, although random network coding has excellent throughput performance, if a receiver obtains an insufficient number of packets, it is extremely unlikely that they can recover any of the original packets.

Applications

Network coding is seen to be useful in the following areas:

Alternative to forward error correction and ARQ in traditional and wireless networks. e.g.: Multi-user ARQ^[5]
Robust and resilient to network attacks like snooping, eavesdropping or replay attacks.^[6]
Digital file distribution and P2P file sharing. e.g.: Avalanche from Microsoft
Throughput increase in wireless mesh networks. e.g. : COPE,^[7] Coding-aware routing^[8]^[9]
Bidirectional low energy transmission in wireless sensor networks.
Many-to-many broadcast network capacity augmentations.
Buffer and Delay reduction in spatial sensor networks: Spatial buffer multiplexing ^[10]
Reduce the number of packet retransmission for a single-hop wireless multicast transmission, and hence improve network bandwidth.^[11]

References

^ S. Li, R. Yeung, and N. Cai, "Linear Network Coding"(PDF), in IEEE Transactions on Information Theory, Vol 49, No. 2, pp. 371–381, 2003
^ R. Dougherty, C. Freiling, and K. Zeger, "Insufficiency of Linear Coding in Network Information Flow" (PDF), in IEEE Transactions on Information Theory, Vol. 51, No. 8, pp. 2745-2759, August 2005 ( erratum)
^ ^a ^b Ahlswede, Rudolf (2000). "Network Information Flow". IEEE Transactions on Information Theory, IT-46. 46 (4): 1204–1216. doi:10.1109/18.850663. {{cite journal}}: Unknown parameter |coauthors= ignored (|author= suggested) (help)
^ T. Ho, R. Koetter, M. Medard, D. R. Karger and M. Effros, "The Benefits of Coding over Routing in a Randomized Setting" in 2003 IEEE International Symposium on Information Theory.
^ http://www.ericsson.com/technology/research_papers/wireless_access/doc/Multi-User%20ARQ.pdf
^ http://home.eng.iastate.edu/~yuzhen/publications/ZhenYu_INFOCOM_2008.pdf
^ Sigcomm 2006 Form >> XORs in The Air: Practical Wireless Network Coding
^ http://arena.cse.sc.edu/papers/rocx.secon06.pdf
^ http://www.cs.wisc.edu/~shravan/infocom-07-2.pdf
^ Welcome to IEEE Xplore 2.0: Looking at Large Networks: Coding vs. Queueing
^ http://ieeexplore.ieee.org/xpl/articleDetails.jsp?arnumber=4549741

Fragouli, C.; Le Boudec, J. & Widmer, J. "Network coding: An instant primer" in Computer Communication Review, 2006.

External links

Network Coding Homepage
A network coding bibliography
An Overview of Network Coding in Broadcast Wireless Communication:[1]
Raymond W. Yeung, Information Theory and Network Coding, Springer 2008, http://iest2.ie.cuhk.edu.hk/~whyeung/book2/
Raymond W. Yeung et al., Network Coding Theory, now Publishers, 2005, http://iest2.ie.cuhk.edu.hk/~whyeung/netcode/monograph.html
Christina Fragouli et al., Network Coding: An Instant Primer, ACM SIGCOMM 2006, http://infoscience.epfl.ch/getfile.py?mode=best&recid=58339.
Avalanche Filesystem, http://research.microsoft.com/en-us/projects/avalanche/default.aspx
Random Network Coding, http://www.mit.edu/~medard/coding1.htm
Digital Fountain Codes, http://www.icsi.berkeley.edu/~luby/
Coding-Aware Routing, http://arena.cse.sc.edu/papers/rocx.secon06.pdf
MIT offers a course: Introduction to Network Coding
Network coding: Networking's next revolution?
Coding-aware protocol design for wireless networks: http://scholarcommons.sc.edu/etd/230/

[1] S. Li, R. Yeung, and N. Cai, "Linear Network Coding"(PDF), in IEEE Transactions on Information Theory, Vol 49, No. 2, pp. 371–381, 2003

[2] R. Dougherty, C. Freiling, and K. Zeger, "Insufficiency of Linear Coding in Network Information Flow" (PDF), in IEEE Transactions on Information Theory, Vol. 51, No. 8, pp. 2745-2759, August 2005 ( erratum)

[Ahlswede2000-3] Ahlswede, Rudolf (2000). "Network Information Flow". IEEE Transactions on Information Theory, IT-46. 46 (4): 1204–1216. doi:10.1109/18.850663. {{cite journal}}: Unknown parameter |coauthors= ignored (|author= suggested) (help)

[Ho2003-4] T. Ho, R. Koetter, M. Medard, D. R. Karger and M. Effros, "The Benefits of Coding over Routing in a Randomized Setting" in 2003 IEEE International Symposium on Information Theory.

[5] ttp://www.ericsson.com/technology/research_papers/wireless_access/doc/Multi-User%20ARQ.pdf

[6] ttp://home.eng.iastate.edu/~yuzhen/publications/ZhenYu_INFOCOM_2008.pdf

[7] Sigcomm 2006 Form >> XORs in The Air: Practical Wireless Network Coding

[8] ttp://arena.cse.sc.edu/papers/rocx.secon06.pdf

[9] ttp://www.cs.wisc.edu/~shravan/infocom-07-2.pdf

[10] Welcome to IEEE Xplore 2.0: Looking at Large Networks: Coding vs. Queueing

[11] ttp://ieeexplore.ieee.org/xpl/articleDetails.jsp?arnumber=4549741

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

@@ Line 6: / Line 6: @@
 In a linear network coding problem, a group of nodes <math>P</math> are involved in moving the data from <math>S</math> source nodes to <math>K</math> sink nodes. Each node generates new packets which are linear combinations of earlier received packets, multiplying them by [[coefficient]]s chosen from a [[Galois field|finite field]], typically of size <math>GF(2^s)</math>.
-Each node, <math>p_k</math> with [[Indegree#Indegree_and_outdegree|in degree, (InDeg)]], <math>InDeg(p_k) = S</math>, generates a  message <math>X_k</math> from the linear combination of received messages <math>\{M_i\}_{i = 1}^S</math> by the relation:
+Each node, <math>p_k</math> with [[Indegree#Indegree_and_outdegree|indegree]], <math>InDeg(p_k) = S</math>, generates a  message <math>X_k</math> from the linear combination of received messages <math>\{M_i\}_{i = 1}^S</math> by the relation:
 :<math>X_k = \sum_{i=1}^S g_k^i\cdot M_i</math>
 where the values <math>g_k^i</math> are the coefficients selected from <math>GF(2^s)</math>. Note that, since operations are computed in a finite field, the generated message is of the same length as the original messages. Each node forwards the computed value <math>X_k</math> along with the coefficients, <math>g_k^i</math>, used in the <math>k^\text{th}</math> level, <math>g_k^i</math>.