Trapezoid: Difference between revisions

Content deleted Content added

Inline

Revision as of 18:43, 24 September 2006

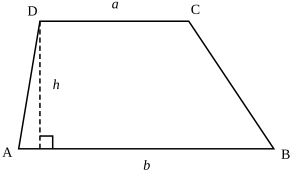
A trapezoid (in North America) or trapezium (in Britain and elsewhere) is a quadrilateral two of whose sides are parallel to each other. Some authors define it as a quadrilateral having exactly one pair of parallel sides, so as to exclude parallelograms.

Note that there is another confusingly-named quadrilateral that has no parallel sides: the trapezoid (North America) or trapezium (Britian and elsewhere). To avoid confusion, this article uses the North American wording, and admits parallelograms as special cases.

In an isosceles trapezoid, the base angles are congruent, and so are the pair of non-parallel opposite sides.

If the other pair of opposite sides is also parallel, then the trapezoid is also a parallelogram. Otherwise, the other two opposite sides may be extended until they meet at a point, forming a triangle that the trapezoid lies inside.

A quadrilateral is a trapezoid if and only if it contains two adjacent angles that are supplementary, that is, they add up to one straight angle of 180 degrees (π radians). Another necessary and sufficient condition is that the diagonals cut each other in mutually the same ratio; this ratio is the same as that between the lengths of the parallel sides.

The midsegment of a tradepoid is the segment that joins the midpoints of the nonparallel opposite sides. It is parallel to the two parallel sides, and its length is the arithmetic mean of the lengths of those sides.

The area of a trapezoid can be computed as the length of the midsegment, multiplied by the distance along a perpendicular line between them. This yields as a special case the well-known formula for the area of a triangle, by considering a triangle as a degenerate trapezoid in which one of the parallel sides has shrunk to a point.

Thus, if a and b are the two parallel sides and h is the distance (height) between the parallels, the area formula is as follows:

A={\frac {(a+b)h}{2}}

Another formula for the area can be used when all that is known are the lengths of the four sides. If the sides are a, b, c and d, and a and c are parallel (where a is the longer parallel side), then:

A={\frac {a+c}{4(a-c)}}{\sqrt {(a+b-c+d)(a-b-c+d)(a+b-c-d)(-a+b+c+d)}}

If the trapezoid above is divided into 4 triangles by its diagonals AC and BD, intersecting at O, then the area of ΔAOD is equal to that of ΔBOC, and the product of the areas of ΔAOD and ΔBOC is equal to that of ΔAOB and ΔCOD. The ratio of the areas of each pair of adjacent triangles is the same as that between the lengths of the parallel sides.

External links

"Trapezoid" on MathWorld
Trapezoid definition Area of a trapezoid Median of a trapezoid With interactive animations
Trapezium (Trapezoid) Interactive Calculator

@@ Line 4: / Line 4: @@
 A '''trapezoid''' (in North America) or '''trapezium''' (in Britain and elsewhere) is a [[quadrilateral]] two of whose sides are [[parallel (geometry)|parallel]] to each other.  Some authors define it as a quadrilateral having ''exactly'' one pair of parallel sides, so as to exclude [[parallelogram]]s.
-:Note that there is another confusingly-named quadrilateral that has no parallel sides: the ''trapezium'' (North America) or ''trapezoid'' (Britian and elsewhere).  To avoid confusion, this article uses the North American wording, and admits parallelograms as special cases.
+:Note that there is another confusingly-named quadrilateral that has no parallel sides: the ''trapezoid'' (North America) or ''trapezium'' (Britian and elsewhere).  To avoid confusion, this article uses the North American wording, and admits parallelograms as special cases.
 In an [[isosceles trapezoid]], the base angles are congruent, and so are the pair of non-parallel opposite sides.