Law of sines

In trigonometry, the law of sines (or sine law) is a statement about arbitrary triangles in the plane. If the sides of the triangle are a, b and c and the angles opposite those sides are A, B and C, then the law of sines states:

${a \over \sin A}={b \over \sin B}={c \over \sin C}=2R\,$

where R is the radius of the triangle's circumcircle. This formula is useful to compute the remaining sides of a triangle if two angles and a side are known, a common problem in the technique of triangulation. It can also be used when two sides and one of the non-enclosed angles are known; in this case, the formula may give two possible values for the enclosed angle. When this happens, often only one result will cause all angles to be less than 180°; in other cases, there are two valid solutions to the triangle (see the ambiguous case section of this article for further information).

It can be shown that:

$2R={\frac {abc}{2{\sqrt {s(s-a)(s-b)(s-c)}}}}={\frac {2abc}{\sqrt {(a^{2}+b^{2}+c^{2})^{2}-2(a^{4}+b^{4}+c^{4})}}}$

where s is the semi-perimeter,

$s={\frac {(a+b+c)}{2}}.$

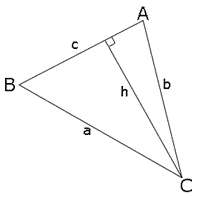
Derivation

Make a triangle with the sides a, b, and c, and angles A, B, and C. Draw a line from the angle C to the side across c so that it divides the original triangle into two right angle triangles. Mark the length of this line h.

It can be observed that:

$\sin B={\frac {c}{a}}$ and $\;\sin B={\frac {h}{a}}.$

Therefore:

$h=b\,(\sin A)=a\,(\sin B)$

and

${\frac {a}{\sin A}}={\frac {b}{\sin B}}.$

Doing the same thing with the line drawn between angle A and side a will yield:

${\frac {b}{\sin B}}={\frac {c}{\sin C}}.$

Full proof:

Make a triangle ABC with sides a, b, c and the γ angle at C. Make an axis through the center of b and another through the c side. Mark the point of intersection of the axis S. Draw a circle k with its center in S with the radius r = |SA| = |SB| = |SC| (the Circumcircle). Through the medial angle law, the angle at S is 2*γ.

Thus, it can be observed that:

$\sin \gamma ={\frac {\frac {c}{2}}{r}}$

or:

$\sin \gamma ={\frac {c}{2r}}$

and then

${\frac {c}{\sin \gamma }}={2r}$

Applying cyclic permutation:

${\frac {a}{\sin \alpha }}={\frac {b}{\sin \beta }}={\frac {c}{\sin \gamma }}={2r}$(č.b.t.d)

Examples

Here is an example of how to solve a problem using the law of sines:

Given: side a = 10, side c = 7, and angle C = 30 degrees

Using the law of sines, we know that :${\frac {a}{\sin A}}={\frac {c}{\sin C}}.$

Plugging in the given values, we find that :${\frac {10}{\sin A}}={\frac {7}{\sin 30}}.$

Simplifying, the sine of angle A is equal to 5/7, or approximately 0.714. Thus, angle A is equal to 45.58 degrees.

Or another example of how to solve a problem using the law of sines:

If two sides of the triangle are equal to R and the length of the third side, the chord, is given as 100' (30.48 m) and the angle C opposite to the chord is given in degrees, then angle A = angle B = :${(180-C) \over 2}$ and

${R \over \sin A}={{\mbox{chord}} \over \sin C}\,$ or ${R \over \sin B}={{\mbox{chord}} \over \sin C}\,$

${{\mbox{chord}}\,\sin A \over \sin C}=R$ or ${{\mbox{chord}}\,\sin B \over \sin C}=R$

This is North American railroad surveying practice.

See also

• Triangulation
• Law of cosines
• Law of tangents
• Surveying

External links

• Excellent tutorial on the law of sines
• The Law of Sines at cut-the-knot
• Degree of Curvature