Analytic signal

Not to be confused with analytic expression or analytic function.

In mathematics and signal processing, an analytic signal is a complex-valued function that has no negative frequency components. It is used to represent a causal signal, that starts at a certain time and propagates as the time evolves, i.e. not backwards in time. This leads to the absence of negative frequencies, which is a side effect, reflecting causality.   The real and imaginary parts of an analytic signal are real-valued functions related to each other by the Hilbert transform.

The analytic representation of a real-valued function is an analytic signal, comprising the original function and its Hilbert transform. This representation facilitates many mathematical manipulations. The basic idea is that the negative frequency components of the Fourier transform (or spectrum) of a real-valued function are superfluous, due to the Hermitian symmetry of such a spectrum. These negative frequency components can be discarded with no loss of information, provided one is willing to deal with a complex-valued function instead. That makes certain attributes of the function more accessible and facilitates the derivation of modulation and demodulation techniques, such as single-sideband.

As long as the manipulated function has no negative frequency components (that is, it is still analytic), the conversion from complex back to real is just a matter of discarding the imaginary part. The analytic representation is a generalization of the phasor concept: while the phasor is restricted to time-invariant amplitude, phase, and frequency, the analytic signal allows for time-variable parameters.

Definition

Transfer function to create an analytic signal

If $s(t)$ is a real-valued (causal) function with Fourier transform $S(f)$, then the transform has Hermitian symmetry about the $f=0$ axis:

$S(-f)=S(f)^{*},$

where $S(f)^{*}$ is the complex conjugate of $S(f)$. The function:

${\begin{aligned}S_{\mathrm {a} }(f)&\triangleq {\begin{cases}2S(f),&{\text{for}}\ f>0,\\S(f),&{\text{for}}\ f=0,\\0,&{\text{for}}\ f<0\end{cases}}\\&=\underbrace {2\operatorname {u} (f)} _{1+\operatorname {sgn}(f)}S(f)=S(f)+\operatorname {sgn}(f)S(f),\end{aligned}}$

where

• $\operatorname {u} (f)$ is the Heaviside step function,
• $\operatorname {sgn}(f)$ is the sign function,

contains only the non-negative frequency components of $S(f)$. And the operation is reversible, due to the Hermitian symmetry of $S(f)$:

${\begin{aligned}S(f)&={\begin{cases}{\frac {1}{2}}S_{\mathrm {a} }(f),&{\text{for}}\ f>0,\\S_{\mathrm {a} }(f),&{\text{for}}\ f=0,\\{\frac {1}{2}}S_{\mathrm {a} }(-f)^{*},&{\text{for}}\ f<0\ {\text{(Hermitian symmetry)}}\end{cases}}\\&={\frac {1}{2}}[S_{\mathrm {a} }(f)+S_{\mathrm {a} }(-f)^{*}].\end{aligned}}$

The analytic signal of $s(t)$ is the inverse Fourier transform of $S_{\mathrm {a} }(f)$:

${\begin{aligned}s_{\mathrm {a} }(t)&\triangleq {\mathcal {F}}^{-1}[S_{\mathrm {a} }(f)]\\&={\mathcal {F}}^{-1}[S(f)+\operatorname {sgn}(f)\cdot S(f)]\\&=\underbrace {{\mathcal {F}}^{-1}\{S(f)\}} _{s(t)}+\overbrace {\underbrace {{\mathcal {F}}^{-1}\{\operatorname {sgn}(f)\}} _{j{\frac {1}{\pi t}}}*\underbrace {{\mathcal {F}}^{-1}\{S(f)\}} _{s(t)}} ^{\text{convolution}}\\&=s(t)+j\underbrace {\left[{1 \over \pi t}*s(t)\right]} _{\operatorname {\mathcal {H}} [s(t)]}\\&=s(t)+j{\hat {s}}(t),\end{aligned}}$

where

• ${\hat {s}}(t)\triangleq \operatorname {\mathcal {H}} [s(t)]$ is the Hilbert transform of $s(t)$;
• $*$ is the convolution symbol;
• $j$ is the imaginary unit.

Noting that $s(t)=s(t)*\delta (t)$ and $\operatorname {\mathcal {H}} [\delta (t)])={1 \over \pi t},$ this can also be expressed as a filtering operation that directly removes negative frequency components:

$s_{\mathrm {a} }(t)=s(t)*\underbrace {\left[\delta (t)+j{1 \over \pi t}\right]} _{{\mathcal {F}}^{-1}\{2u(f)\}}=s(t)*(\delta (t)+j\operatorname {\mathcal {H}} [\delta (t)])=s(t)*(\delta (t)+j\delta (j\cdot t)).$

It is important, that in all definitions, the support in the time domain for the analytic signal is $\left[0,+\infty \right[$, meaning it is zero otherwise. The critical assumption for the derivation is the aforementioned convolution $s(t)=s(t)*\delta (t)$, which is only valid, if the real part of the signal is causal. Since the imaginary part is the convolution with the Hilbert Transform of a dirac delta, this implies causality for the imaginary part as well. This leads to a consistent coupling between real and imaginary part for the whole time axis. Since $s_{\mathrm {a} }(t)$ is analytic, the behaviour of its absolut value at the singularity at $t=0$ is physically well defined and is always zero. The convergence of its phase depends on the signal type. Again due to the analytic property, $s_{\mathrm {a} }(t)$ has no bias, i.e. $S_{\mathrm {a} }(0)=0$. These last two properties are crucial, since they provide a deep link between theoretical results in signal processing and physical realization issues, that are not always considered. Especially in modulation schemes, the transition behaviour between symbols (e.g. of a pulse train) has to be consistent with these properties when they are operated in regimes, that are close to these fundamental restrictions. This is a consequence of the Hilbert Transform (and its subtle definition) and cannot be seen when plotting it.

Interpretation of the analytic signal

It describes a physically realizable signal with a starting point and finite energy. Since the imaginary part is the Hilbert Transform of the real part, it is redundant, meaning it is fully described by the real part. The same is true vice versa, since the Hilbert Transform is invertible. The whole complex plane consisting of the real and imaginary part of the (theoretical) analytic signal is therefore completely defined (in the causal region with positive frequencies). By evaluating $s_{\mathrm {a} }(t)=s(t)*(\delta (t)+j\delta (j\cdot t))$ on the diagonal with equal real and imaginary parts (i.e. letting $t$ start from zero), the complex plane is evaluated at this line and the values for the real and imaginary part of the function are reported. The two dirac deltas will start the signal at $t=0$ by stimulating it with all (positive) frequencies. This leads to a resonance with the signal, which "brings it to life". One stimulates it with the real frequencies and the other with the imaginary frequencies (for the Hilbert Transformed part). Nobody cares what happend before $t=0$, so no memory should be included. The speed with which one varies the time parameter is related to the frequency of the signal. This describes the signals behaviour at a fixed location. If a spatial description of a wave is needed, one needs to encode the position parameter as well as the propagation speed in the free input parameter $t$.

Negative frequency components

Since $s(t)=\operatorname {Re} [s_{\mathrm {a} }(t)]$, restoring the negative frequency components is a simple matter of discarding $\operatorname {Im} [s_{\mathrm {a} }(t)]$ which may seem counter-intuitive. We can also note that the complex conjugate $s_{\mathrm {a} }^{*}(t)$ comprises only the negative frequency components. And therefore $s(t)=\operatorname {Re} [s_{\mathrm {a} }^{*}(t)]$ restores the suppressed positive frequency components. Another viewpoint is that the imaginary component in either case is a term that subtracts frequency components from s(t). The $\operatorname {Re}$ operator removes the subtraction, giving the appearance of adding new components.

Examples

Example 1

$s(t)=\cos(\omega t),$   where  $\omega >0.$

Then:

${\hat {s}}(t)=\cos \left(\omega t-{\frac {\pi }{2}}\right)=\sin(\omega t),$

$s_{\mathrm {a} }(t)=s(t)+j{\hat {s}}(t)=\cos(\omega t)+j\sin(\omega t)=e^{j\omega t}.$  The third equality is Euler's formula.

A corollary of Euler's formula is  $\cos(\omega t)={\tfrac {1}{2}}\left(e^{j\omega t}+e^{j(-\omega )t}\right).$  In general, the analytic representation of a simple sinusoid is obtained by expressing it in terms of complex-exponentials, discarding the negative frequency component, and doubling the positive frequency component. And the analytic representation of a sum of sinusoids is the sum of the analytic representations of the individual sinusoids.

Example 2

Here we use Euler's formula to identify and discard the negative frequency.

$s(t)=\cos(\omega t+\theta )={\frac {1}{2}}\left(e^{j(\omega t+\theta )}+e^{-j(\omega t+\theta )}\right)$

Then:

$s_{\mathrm {a} }(t)={\begin{cases}e^{j(\omega t+\theta )}\ \ =\ e^{j|\omega |t}\cdot e^{j\theta },&{\text{if}}\ \omega >0,\\e^{-j(\omega t+\theta )}=\ e^{j|\omega |t}\cdot e^{-j\theta },&{\text{if}}\ \omega <0.\end{cases}}$

Example 3

This is another example of using the Hilbert transform method to remove negative frequency components. We note that nothing prevents us from computing $s_{\mathrm {a} }(t)$ for a complex-valued $s(t)$. But it might not be a reversible representation, because the original spectrum is not symmetrical in general. So except for this example, the general discussion assumes real-valued $s(t)$.

$s(t)=e^{-j\omega t}$, where $\omega >0$.

Then:

${\hat {s}}(t)=je^{-j\omega t},$

$s_{\mathrm {a} }(t)=e^{-j\omega t}+j^{2}e^{-j\omega t}=e^{-j\omega t}-e^{-j\omega t}=0.$

Properties

Instantaneous amplitude and phase

A function in blue and the magnitude of its analytic representation in red, showing the envelope effect.

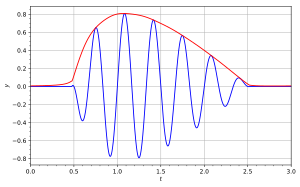
An analytic signal can also be expressed in polar coordinates:

$s_{\mathrm {a} }(t)=s_{\mathrm {m} }(t)e^{j\phi (t)},$

where the following time-variant quantities are introduced:

• $s_{\mathrm {m} }(t)\triangleq |s_{\mathrm {a} }(t)|$ is called the instantaneous amplitude or the envelope;
• $\phi (t)\triangleq \arg \!\left[s_{\mathrm {a} }(t)\right]$ is called the instantaneous phase or phase angle.

In the accompanying diagram, the blue curve depicts $s(t)$ and the red curve depicts the corresponding $s_{\mathrm {m} }(t)$.

The time derivative of the unwrapped instantaneous phase has units of radians/second, and is called the instantaneous angular frequency:

$\omega (t)\triangleq {\frac {d\phi }{dt}}(t).$

The instantaneous frequency (in hertz) is therefore:

$f(t)\triangleq {\frac {1}{2\pi }}\omega (t).$  

The instantaneous amplitude, and the instantaneous phase and frequency are in some applications used to measure and detect local features of the signal. Another application of the analytic representation of a signal relates to demodulation of modulated signals. The polar coordinates conveniently separate the effects of amplitude modulation and phase (or frequency) modulation, and effectively demodulates certain kinds of signals.

Complex envelope/baseband

Analytic signals are often shifted in frequency (down-converted) toward 0 Hz, possibly creating [non-symmetrical] negative frequency components:

${s_{\mathrm {a} }}_{\downarrow }(t)\triangleq s_{\mathrm {a} }(t)e^{-j\omega _{0}t}=s_{\mathrm {m} }(t)e^{j(\phi (t)-\omega _{0}t)},$

where $\omega _{0}$ is an arbitrary reference angular frequency.

This function goes by various names, such as complex envelope and complex baseband. The complex envelope is not unique; it is determined by the choice of $\omega _{0}$. This concept is often used when dealing with passband signals. If $s(t)$ is a modulated signal, $\omega _{0}$ might be equated to its carrier frequency.

In other cases, $\omega _{0}$ is selected to be somewhere in the middle of the desired passband. Then a simple low-pass filter with real coefficients can excise the portion of interest. Another motive is to reduce the highest frequency, which reduces the minimum rate for alias-free sampling. A frequency shift does not undermine the mathematical tractability of the complex signal representation. So in that sense, the down-converted signal is still analytic. However, restoring the real-valued representation is no longer a simple matter of just extracting the real component. Up-conversion may be required, and if the signal has been sampled (discrete-time), interpolation (upsampling) might also be necessary to avoid aliasing.

If $\omega _{0}$ is chosen larger than the highest frequency of $s_{\mathrm {a} }(t),$ then ${s_{\mathrm {a} }}_{\downarrow }(t)$ has no positive frequencies. In that case, extracting the real component restores them, but in reverse order; the low-frequency components are now high ones and vice versa. This can be used to demodulate a type of single sideband signal called lower sideband or inverted sideband.

Other choices of reference frequency

Sometimes $\omega _{0}$ is chosen to minimize

$\int _{0}^{+\infty }(\omega -\omega _{0})^{2}|S_{\mathrm {a} }(\omega )|^{2}\,d\omega .$

Alternatively, $\omega _{0}$ can be chosen to minimize the mean square error in linearly approximating the unwrapped instantaneous phase $\phi (t)$:

$\int _{-\infty }^{+\infty }[\omega (t)-\omega _{0}]^{2}|s_{\mathrm {a} }(t)|^{2}\,dt$

or another alternative (for some optimum $\theta$):

$\int _{-\infty }^{+\infty }[\phi (t)-(\omega _{0}t+\theta )]^{2}\,dt.$

In the field of time-frequency signal processing, it was shown that the analytic signal was needed in the definition of the Wigner–Ville distribution so that the method can have the desirable properties needed for practical applications.

Sometimes the phrase "complex envelope" is given the simpler meaning of the complex amplitude of a (constant-frequency) phasor; other times the complex envelope $s_{m}(t)$ as defined above is interpreted as a time-dependent generalization of the complex amplitude. Their relationship is not unlike that in the real-valued case: varying envelope generalizing constant amplitude.

Extensions of the analytic signal to signals of multiple variables

The concept of analytic signal is well-defined for signals of a single variable which typically is time. For signals of two or more variables, an analytic signal can be defined in different ways, and two approaches are presented below.

Multi-dimensional analytic signal based on an ad hoc direction

A straightforward generalization of the analytic signal can be done for a multi-dimensional signal once it is established what is meant by negative frequencies for this case. This can be done by introducing a unit vector ${\boldsymbol {\hat {u}}}$ in the Fourier domain and label any frequency vector ${\boldsymbol {\xi }}$ as negative if ${\boldsymbol {\xi }}\cdot {\boldsymbol {\hat {u}}}<0$. The analytic signal is then produced by removing all negative frequencies and multiply the result by 2, in accordance to the procedure described for the case of one-variable signals. However, there is no particular direction for ${\boldsymbol {\hat {u}}}$ which must be chosen unless there are some additional constraints. Therefore, the choice of ${\boldsymbol {\hat {u}}}$ is ad hoc, or application specific.

The monogenic signal

The real and imaginary parts of the analytic signal correspond to the two elements of the vector-valued monogenic signal, as it is defined for one-variable signals. However, the monogenic signal can be extended to arbitrary number of variables in a straightforward manner, producing an (n + 1)-dimensional vector-valued function for the case of n-variable signals.

See also

• Practical considerations for computing Hilbert transforms
• Negative frequency

Applications

• Single sideband modulation
• Quadrature filter
• Causal filter

Further reading

• Leon Cohen, Time-frequency analysis, Prentice Hall, Upper Saddle River, 1995.
• Frederick W. King, Hilbert Transforms, vol. II, Cambridge University Press, Cambridge, 2009.
• B. Boashash, Time-Frequency Signal Analysis and Processing: A Comprehensive Reference, Elsevier Science, Oxford, 2003.

External links

• Analytic Signals and Hilbert Transform Filters