Foias constant
In mathematical analysis, the Foias constant is a real number named after Ciprian Foias.
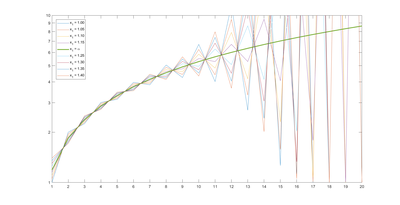
It is defined in the following way: for every real number x1 > 0, there is a sequence defined by the recurrence relation
for n = 1, 2, 3, .... The Foias constant is the unique choice α such that if x1 = α then the sequence diverges to infinity. For all other values of x1, the sequence is divergent as well, but it has two accumulation points: 1 and infinity.[1] Numerically, it is
- .[2]
No closed form for the constant is known.
When x1 = α then the growth rate of the sequence (xn) is given by the limit
where "log" denotes the natural logarithm.[1]
The same methods used in the proof of the uniqueness of the Foias constant may also be applied to other similar recursive sequences.[3]
See also
Notes and references
- ^ a b Ewing, J. and Foias, C. "An Interesting Serendipitous Real Number." In Finite versus Infinite: Contributions to an Eternal Dilemma (Ed. C. Caluse and G. Păun). London: Springer-Verlag, pp. 119–126, 2000.
- ^ Sloane, N. J. A. (ed.). "Sequence A085848 (Decimal expansion of Foias's Constant)". The On-Line Encyclopedia of Integer Sequences. OEIS Foundation.
- ^ Anghel, Nicolae (2018), "Foias numbers" (PDF), An. Ştiinţ. Univ. "Ovidius" Constanţa Ser. Mat., 26 (3): 21–28, doi:10.2478/auom-2018-0030, S2CID 195842026
- S. R. Finch (2003). Mathematical Constants. Cambridge University Press. p. 430. ISBN 0-521-818-052.
Foias constant.








