e (mathematical constant)

e is the unique number such that the value of the derivative (slope of a tangent line) of f (x)=e^x (blue curve) at the point x=0 is exactly 1. For comparison, functions 2^x (dotted curve) and 4^x (dashed curve) are shown; they are not tangent to the line of slope 1 (red).

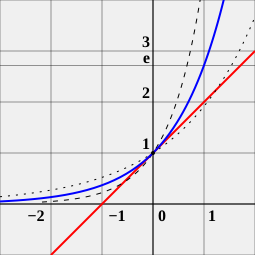
The mathematical constant e is the base of the natural logarithm. It is occasionally called Euler's number after the Swiss mathematician Leonhard Euler, or Napier's constant in honor of the Scottish mathematician John Napier who introduced logarithms. (e is not to be confused with γ – the Euler-Mascheroni constant, sometimes called simply Euler's constant.) The number e is one of the most important numbers in mathematics, alongside the additive and multiplicative identities 0 and 1, the imaginary unit i, and π, the circumference to diameter ratio for any circle. It has a number of equivalent definitions; some of them are given below.

Since e is transcendental, and therefore irrational, its value cannot be given exactly. The numerical value of e truncated to 20 decimal places is:

2.71828 18284 59045 23536

Definitions

The three most common definitions of e are listed below.

1. The limit

   $e=\lim _{n\to \infty }\left(1+{\frac {1}{n}}\right)^{n}$

2. The sum of the infinite series

   $e=\sum _{n=0}^{\infty }{\frac {1}{n!}}={\frac {1}{0!}}+{\frac {1}{1!}}+{\frac {1}{2!}}+{\frac {1}{3!}}+{\frac {1}{4!}}+\cdots$

   where n! is the factorial of n.

3. The unique real number e > 0 such that

   $\int _{1}^{e}{\frac {1}{t}}\,dt={1}$

   (that is, the number e such that the area under the hyperbola $f(t)=1/t$ from 1 to e is equal to 1).

These definitions can be proven to be equivalent.

History

The first references to the constant were published in 1618 in the table of an appendix of a work on logarithms by John Napier. However, this did not contain the constant itself, but simply a list of natural logarithms calculated from the constant. It is assumed that the table was written by William Oughtred. The first indication of e as a constant was discovered by Jacob Bernoulli, trying to find the value of the following expression:

$\lim _{n\to \infty }\left(1+{\frac {1}{n}}\right)^{n}$

The first known use of the constant, represented by the letter b, was in correspondence from Gottfried Leibniz to Christiaan Huygens in 1690 and 1691. Leonhard Euler started to use the letter e for the constant in 1727, and the first use of e in a publication was Euler's Mechanica (1736). While in the subsequent years some researchers used the letter c, e was more common and eventually became the standard.

The exact reasons for the use of the letter e are unknown, but it may be because it is the first letter of the word exponential. Another possibility is that Euler used it because it was the first vowel after a, which he was already using for another number, but his reason for using vowels is unknown. It is unlikely that Euler chose the letter because it is his last initial, since he was a very modest man, and tried to give proper credit to the work of others.

The compound-interest problem

Jacob Bernoulli discovered this constant by studying a question about compound interest.

One simple example is an account that starts with $1.00 and pays 100% interest per year. If the interest is credited once, at the end of the year, the value is $2.00; but if the interest is computed and added twice in the year, the $1 is multiplied by 1.5 twice, yielding $1.00×1.5² = $2.25. Compounding quarterly yields $1.00×1.25⁴ = $2.4414…, and compounding monthly yields $1.00×(1.0833…)¹² = $2.613035….

Bernoulli noticed that this sequence approaches a limit for more and smaller compounding intervals. Compounding weekly yields $2.692597…, while compounding daily yields $2.714567…, just two cents more. Using n as the number of compounding intervals, with interest of 1/n in each interval, the limit for large n is the number that came to be known as e; with continuous compounding, the account value will reach $2.7182818…. More generally, an account that starts at $1, and yields $(1+R) at simple interest, will yield $ e^R with continuous compounding.

Properties

The exponential function f(x) = e^x is important in part because it is the unique nontrivial function (up to multiplication by a constant) which is its own derivative, and therefore, its own primitive:

${\frac {d}{dx}}e^{x}=e^{x}$

and

$e^{x}=1+\int _{0}^{x}e^{t}\,dt.$

e is irrational, and furthermore is transcendental (Lindemann-Weierstrass theorem). It was the first number to be proved transcendental without having been specifically constructed for this purpose (cf. Liouville number); the proof was given by Charles Hermite in 1873. It is conjectured to be normal. It features in Euler's formula, one of the most important formulas in mathematics:

$e^{ix}=\cos x+i\sin x,\,\!$

described by Richard Feynman (p. I-22-10) as "[...] the most remarkable formula in mathematics [...], our jewel."

The special case with x = π is known as Euler's identity:

$e^{i\pi }+1=0.\,\!$

Euler also showed that the infinite tetration

$x^{x^{\cdot ^{\cdot ^{\cdot }}}},$

converges only if $e^{-e}\leq x\leq e^{1/e}.$

The number e is where the global maximum occurs for the function

$f(x)=x^{1 \over x}.$

The value of this function at e is

$f(e)\approx 1.444667861...$

More generally, $\!\ {\sqrt[{n}]{e}}$ is where the global maximum occurs for the function

$\!\ f(x)=x^{1 \over {x^{n}}}$

$e^{x}$ is defined as

$e^{x}=1+{x \over 1!}+{x^{2} \over 2!}+{x^{3} \over 3!}+...{x^{n} \over n!}$

Representations of e

As a continued fraction

The number e can be represented as an infinite simple continued fraction (sequence A003417 in the OEIS):

$e=[2;1,{\textbf {2}},1,1,{\textbf {4}},1,1,{\textbf {6}},1,1,{\textbf {8}},1,\ldots ,1,{\textbf {2n}},1,\ldots ]\,$

Here are some infinite generalized continued fraction expansions of e. The second of these can be generated from the first by a simple equivalence transformation. The third one – with ... 6, 10, 14, ... in it – converges very quickly.

$e=2+{\cfrac {1}{1+{\cfrac {1}{2+{\cfrac {2}{3+{\cfrac {3}{4+{\cfrac {4}{\ddots }}}}}}}}}}\qquad e=2+{\cfrac {2}{2+{\cfrac {3}{3+{\cfrac {4}{4+{\cfrac {5}{5+{\cfrac {6}{\ddots \,}}}}}}}}}}$

$e=1+{\cfrac {2}{1+{\cfrac {1}{6+{\cfrac {1}{10+{\cfrac {1}{14+{\cfrac {1}{\ddots \,}}}}}}}}}}$

$e^{2m/n}=1+{\cfrac {2m}{(n-m)+{\cfrac {m^{2}}{3n+{\cfrac {m^{2}}{5n+{\cfrac {m^{2}}{7n+{\cfrac {m^{2}}{\ddots \,}}}}}}}}}}$

Setting m=x and n=2 yields

$e^{x}=1+{\cfrac {2x}{(2-x)+{\cfrac {x^{2}}{6+{\cfrac {x^{2}}{10+{\cfrac {x^{2}}{14+{\cfrac {x^{2}}{\ddots \,}}}}}}}}}}$

As an infinite series

The number e is also equal to the sum of the following infinite series:

$e=\left[\sum _{k=0}^{\infty }{\frac {(-1)^{k}}{k!}}\right]^{-1}$

$e=\left[\sum _{k=0}^{\infty }{\frac {1-2k}{(2k)!}}\right]^{-1}$

$e={\frac {1}{2}}\sum _{k=0}^{\infty }{\frac {k+1}{k!}}$

$e=2\sum _{k=0}^{\infty }{\frac {k+1}{(2k+1)!}}$

$e=\sum _{k=0}^{\infty }{\frac {3-4k^{2}}{(2k+1)!}}$

$e=\sum _{k=0}^{\infty }{\frac {(3k)^{2}+1}{(3k)!}}$

$e=\left[\sum _{k=0}^{\infty }{\frac {4k+3}{2^{2k+1}\,(2k+1)!}}\right]^{2}$

$e=-{\frac {12}{\pi ^{2}}}\left[\sum _{k=1}^{\infty }{\frac {1}{k^{2}}}\ \cos \left({\frac {9}{k\pi +{\sqrt {k^{2}\pi ^{2}-9}}}}\right)\right]^{-1/3}$

$e=\sum _{k=1}^{\infty }{\frac {k^{2}}{2(k!)}}$

$e=\sum _{k=1}^{\infty }{\frac {k^{3}}{5(k!)}}$

$e=\sum _{k=1}^{\infty }{\frac {k^{4}}{15(k!)}}$

$e=\sum _{k=1}^{\infty }{\frac {k^{n}}{B_{n}(k!)}}$ where $B_{n}$ is the $n^{th}$ Bell number.

As an infinite product

The number e is also given by several infinite product forms including Pippenger's product

$e=2\left({\frac {2}{1}}\right)^{1/2}\left({\frac {2}{3}}\;{\frac {4}{3}}\right)^{1/4}\left({\frac {4}{5}}\;{\frac {6}{5}}\;{\frac {6}{7}}\;{\frac {8}{7}}\right)^{1/8}\cdots$

and Guillera's product (see Sondow, 2005)

$e=\left({\frac {2}{1}}\right)^{1/1}\left({\frac {2^{2}}{1\cdot 3}}\right)^{1/2}\left({\frac {2^{3}\cdot 4}{1\cdot 3^{3}}}\right)^{1/3}\left({\frac {2^{4}\cdot 4^{4}}{1\cdot 3^{6}\cdot 5}}\right)^{1/4}\cdots ,$

where the nth factor is the nth root of the product

$\prod _{k=0}^{n}(k+1)^{(-1)^{k+1}{n \choose k}},$

as well as the infinite product

$e={\frac {2\cdot 2^{(\ln(2)-1)^{2}}\cdots }{2^{\ln(2)-1}\cdot 2^{(\ln(2)-1)^{3}}\cdots }}.$

As the limit of a sequence

The number e is equal to the limit of several infinite sequences:

$e=\lim _{n\to \infty }n\cdot \left({\frac {\sqrt {2\pi n}}{n!}}\right)^{1/n}$ and

$e=\lim _{n\to \infty }{\frac {n}{\sqrt[{n}]{n!}}}$ (both by Stirling's formula).

The symmetric limit,

$e=\lim _{n\to \infty }\left[{\frac {(n+1)^{n+1}}{n^{n}}}-{\frac {n^{n}}{(n-1)^{n-1}}}\right]$

may be obtained by manipulation of the basic limit definition of e. Another limit is

$e=\lim _{n\to \infty }(p_{n}\#)^{1/p_{n}}$

where $p_{n}$ is the nth prime and $p_{n}\#$ is the primorial of the nth prime.

Non-mathematical uses of e

One of the most famous mathematical constants, e is also frequently referenced outside of mathematics. Some examples are:

• In the IPO filing for Google, in 2004, rather than a typical round-number amount of money, the company announced its intention to raise $2,718,281,828, which is e billion dollars to the nearest dollar.

• Google was also responsible for a mysterious billboard that appeared in the heart of Silicon Valley, and later in Cambridge, Massachusetts; Seattle, Washington; and Austin, Texas. It read {first 10-digit prime found in consecutive digits of e}.com. Solving this problem and visiting the web site advertised led to an even more difficult problem to solve, which in turn leads to Google Labs where the visitor is invited to submit a resume. The first 10-digit prime in e is 7427466391, which surprisingly starts as late as at the 101st digit. (A random stream of digits has a 98.4% chance of starting a 10-digit prime sooner.)

• The famous computer scientist Donald Knuth let the version numbers of his program METAFONT approach e (the versions are 2, 2.7, 2.71, 2.718, etc.).

References

• Maor, Eli; e: The Story of a Number, ISBN 0-691-05854-7

External links

• The number e to 1 million places and 2, 5 or 10 million places
• Earliest Uses of Symbols for Constants
• e the EXPONENTIAL - the Magic Number of GROWTH - Keith Tognetti, University of Wollongong, NSW, Australia