Metallic mean

Metallic means (Metallic ratios)			Class
N	Ratio	Value	Name (type)
0	⁠0 + √4/2⁠	1
1	⁠1 + √5/2⁠	1.618033989	Golden
2	⁠2 + √8/2⁠	2.414213562	Silver
3	⁠3 + √13/2⁠	3.302775638	Bronze
4	⁠4 + √20/2⁠	4.236067978
5	⁠5 + √29/2⁠	5.192582404
6	⁠6 + √40/2⁠	6.162277660
7	⁠7 + √53/2⁠	7.140054945
8	⁠8 + √68/2⁠	8.123105626
9	⁠9 + √85/2⁠	9.109772229
10	⁠10+ √104/2⁠	10.099019513
⋮
n	⁠n + √n2+4/2⁠

Golden ratio within the pentagram and silver ratio within the octagon.

The metallic means (also ratios or constants) of the successive natural numbers are the continued fractions:

$n+{\cfrac {1}{n+{\cfrac {1}{n+{\cfrac {1}{n+{\cfrac {1}{n+\ddots \,}}}}}}}}=[n;n,n,n,n,\dots ]={\frac {n+{\sqrt {n^{2}+4}}}{2}}.$

The golden ratio (1.618...) is the metallic mean between 1 and 2, while the silver ratio (2.414...) is the metallic mean between 2 and 3. The term "bronze ratio" (3.303...), or terms using other names of metals (such as copper or nickel), are occasionally used to name subsequent metallic means. The values of the first ten metallic means are shown at right. Notice that each metallic mean is a root of the simple quadratic equation: $x^{2}-nx=1$, where $n$ is any positive natural number.

As the golden ratio is connected to the pentagon (first diagonal/side), the silver ratio is connected to the octagon (second diagonal/side). As the golden ratio is connected to the Fibonacci numbers, the silver ratio is connected to the Pell numbers, and the bronze ratio is connected to OEIS: A006190. Each Fibonacci number is the sum of the previous number times one plus the number before that, each Pell number is the sum of the previous number times two and the one before that, and each "bronze Fibonacci number" is the sum of the previous number times three plus the number before that. Taking successive Fibonacci numbers as ratios, these ratios approach the golden mean, the Pell number ratios approach the silver mean, and the "bronze Fibonacci number" ratios approach the bronze mean.

Properties

If one removes the largest possible square from the end of a gold rectangle one is left with a gold rectangle. If one removes two from a silver, one is left with a silver. If one removes three from a bronze, one is left with a bronze. Examine the dotted lines representing the boundaries of the perfect squares within each rectangle, and note that the number of said dotted lines always equals N.

Gold, silver, and bronze ratios within their respective rectangles.

These properties are valid only for integers m. For nonintegers the properties are similar but slightly different.

The above property for the powers of the silver ratio is a consequence of a property of the powers of silver means. For the silver mean S of m, the property can be generalized as

$S_{m}^{n}=K_{n}S_{m}+K_{(n-1)}$

where

$K_{n}=mK_{(n-1)}+K_{(n-2)}.$

Using the initial conditions K₀ = 1 and K₁ = m, this recurrence relation becomes

$K_{n}={\frac {S_{m}^{n+1}-{\left(m-S_{m}\right)}^{n+1}}{\sqrt {m^{2}+4}}}.$

The powers of silver means have other interesting properties:

If n is a positive even integer:

${S_{m}^{n}-\left\lfloor S_{m}^{n}\right\rfloor }=1-S_{m}^{-n}.$

Additionally,

${1 \over {S_{m}^{4}-\left\lfloor S_{m}^{4}\right\rfloor }}+\left\lfloor S_{m}^{4}-1\right\rfloor =S_{\left(m^{4}+4m^{2}+1\right)}$

${1 \over {S_{m}^{6}-\left\lfloor S_{m}^{6}\right\rfloor }}+\left\lfloor S_{m}^{6}-1\right\rfloor =S_{\left(m^{6}+6m^{4}+9m^{2}+1\right)}.$

A golden triangle. The ratio a:b is equivalent to the golden ratio φ. In a silver triangle this would be equivalent to δ_S.

Also,

$S_{m}^{3}=S_{\left(m^{3}+3m\right)}$

$S_{m}^{5}=S_{\left(m^{5}+5m^{3}+5m\right)}$

$S_{m}^{7}=S_{\left(m^{7}+7m^{5}+14m^{3}+7m\right)}$

$S_{m}^{9}=S_{\left(m^{9}+9m^{7}+27m^{5}+30m^{3}+9m\right)}$

$S_{m}^{11}=S_{\left(m^{11}+11m^{9}+44m^{7}+77m^{5}+55m^{3}+11m\right)}.$

In general:

$S_{m}^{2n+1}=S_{\sum _{k=0}^{n}{{2n+1} \over {2k+1}}{{n+k} \choose {2k}}m^{2k+1}}.$

The silver mean S of m also has the property that

${\frac {1}{S_{m}}}=S_{m}-m$

meaning that the inverse of a silver mean has the same decimal part as the corresponding silver mean.

$S_{m}=a+b$

where a is the integer part of S and b is the decimal part of S, then the following property is true:

$S_{m}^{2}=a^{2}+mb+1.$

Because (for all m greater than 0), the integer part of S_m = m, a = m. For m > 1, we then have

$S_{m}^{2}=ma+mb+1$

$S_{m}^{2}=m(a+b)+1$

$S_{m}^{2}=m\left(S_{m}\right)+1.$

Therefore, the silver mean of m is a solution of the equation

$x^{2}-mx-1=0.$

It may also be useful to note that the silver mean S of −m is the inverse of the silver mean S of m

${\frac {1}{S_{m}}}=S_{(-m)}=S_{m}-m.$

Another interesting result can be obtained by slightly changing the formula of the silver mean. If we consider a number

${\frac {n+{\sqrt {n^{2}+4c}}}{2}}=R$

then the following properties are true:

$R-\lfloor R\rfloor ={\frac {c}{R}}$ if c is real,

$\left({1 \over R}\right)c=R-\lfloor \operatorname {Re} (R)\rfloor$ if c is a multiple of i.

The silver mean of m is also given by the integral

$S_{m}=\int _{0}^{m}{\left({x \over {2{\sqrt {x^{2}+4}}}}+{{m+2} \over {2m}}\right)}\,dx.$

Another interesting form of the metallic mean is given by

${\frac {n+{\sqrt {n^{2}+4}}}{2}}=e^{\operatorname {arsinh(n/2)} }$

Trigonometric expressions

N	Trigonometric expression	Associated regular polygon
1	$2\cos {\frac {\pi }{5}}$	pentagon
2	$\tan {\frac {3\pi }{8}}$	octagon
3	$8\cos {\frac {\pi }{13}}\cos {\frac {3\pi }{13}}\cos {\frac {4\pi }{13}}$	tridecagon
4	$8\cos ^{3}{\frac {\pi }{5}}$	pentagon
5	$128\cos {\frac {\pi }{29}}\cos {\frac {4\pi }{29}}\cos {\frac {5\pi }{29}}\cos {\frac {6\pi }{29}}\cos {\frac {7\pi }{29}}\cos {\frac {9\pi }{29}}\cos {\frac {13\pi }{29}}$	29-gon
6	${\frac {\sin {\frac {21\pi }{40}}}{\sin {\frac {7\pi }{8}}-\sin {\frac {5\pi }{8}}\sin {\frac {\pi }{40}}\csc {\frac {11\pi }{40}}-\sin {\frac {19\pi }{20}}\sin {\frac {9\pi }{40}}\csc {\frac {7\pi }{10}}}}$	tetracontagon
7
8	${\frac {\sin {\frac {6\pi }{17}}\sin {\frac {7\pi }{17}}\sin {\frac {3\pi }{17}}\sin {\frac {12\pi }{17}}}{\sin {\frac {\pi }{17}}\sin {\frac {9\pi }{17}}\sin {\frac {4\pi }{17}}\sin {\frac {2\pi }{17}}}}$	heptadecagon
9
10

Geometric construction

The metallic mean for any given integer $N$ can be constructed geometrically in the following way. Define a right triangle with sides $A$ and $B$ having lengths of $1$ and $N/2$, respectively. The $N$th metallic mean $M$ is simply the sum of the length of $B$ and the hypotenuse, $H$.

For $N=1$,

N = 1

$H={\sqrt {(N/2)^{2}+1^{2}}}={\sqrt {5/4}}=1.1180339...$

and so

$M=B+H=1/2+1.1180339...=1.6180339...=$ φ.

Setting $N=2$ yields the silver ratio.

N = 2

$H={\sqrt {(2/2)^{2}+1^{2}}}={\sqrt {2}}=1.4142135...$

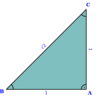
Thus

$M=B+H=2/2+1.4142135...=2.4142135...$

Likewise, the bronze ratio would be calculated with $N=3$ so

N = 3

$H={\sqrt {(3/2)^{2}+1^{2}}}={\sqrt {13/4}}=1.8027756...$

yields

$M=B+H=3/2+1.8027756...=3.3027756...$

Non-integer arguments sometimes produce triangles with a mean that is itself an integer. Examples include N = 1.5, where

N = 1.5

$H={\sqrt {(1.5/2)^{2}+1^{2}}}={\sqrt {1.5625}}=1.25$

and

$M=B+H=1.5/2+1.25=2$

which is simply a scaled-down version of the 3–4–5 Pythagorean triangle.

See also

• Constant
• Mean
• Ratio
• Plastic ratio

Notes

 k. OEIS: A084844, Denominators of the continued fraction n + 1/(n + 1/...) [n times].

Further reading

• Stakhov, Alekseĭ Petrovich (2009). The Mathematics of Harmony: From Euclid to Contemporary Mathematics and Computer Science, p. 228, 231. World Scientific. ISBN 9789812775832.

External links

• Cristina-Elena Hrețcanu and Mircea Crasmareanu (2013). "Metallic Structures on Riemannian Manifolds", Revista de la Unión Matemática Argentina.
• Rakočević, Miloje M. "Further Generalization of Golden Mean in Relation to Euler's 'Divine' Equation", Arxiv.org.