Golden triangle (mathematics)


A golden triangle, also called a sublime triangle,[1] is an isosceles triangle in which the duplicated side is in the golden ratio to the base side:
Angles[edit]
- Hence the golden triangle is an acute (isosceles) triangle.
- Since the angles of a triangle sum to radians, each of the base angles (CBX and CXB) is:
- Note:
- The golden triangle is uniquely identified as the only triangle to have its three angles in the ratio 1 : 2 : 2 (36°, 72°, 72°).[3]
In other geometric figures[edit]

- Golden triangles can be found in the spikes of regular pentagrams.
- Golden triangles can also be found in a regular decagon, an equiangular and equilateral ten-sided polygon, by connecting any two adjacent vertices to the center. This is because: 180(10−2)/10 = 144° is the interior angle, and bisecting it through the vertex to the center: 144/2 = 72°.[1]
- Also, golden triangles are found in the nets of several stellations of dodecahedrons and icosahedrons.
Logarithmic spiral[edit]

The golden triangle is used to form some points of a logarithmic spiral. By bisecting one of the base angles, a new point is created that in turn, makes another golden triangle.[4] The bisection process can be continued indefinitely, creating an infinite number of golden triangles. A logarithmic spiral can be drawn through the vertices. This spiral is also known as an equiangular spiral, a term coined by René Descartes. "If a straight line is drawn from the pole to any point on the curve, it cuts the curve at precisely the same angle," hence equiangular.[5] This spiral is different from the golden spiral: the golden spiral grows by a factor of the golden ratio in each quarter-turn, whereas the spiral through these golden triangles takes an angle of 108° to grow by the same factor.[6]
Golden gnomon[edit]
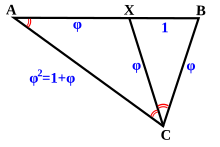

Closely related to the golden triangle is the golden gnomon, which is the isosceles triangle in which the ratio of the equal side lengths to the base length is the reciprocal of the golden ratio .
"The golden triangle has a ratio of base length to side length equal to the golden section φ, whereas the golden gnomon has the ratio of side length to base length equal to the golden section φ."[7]
Angles[edit]
(The distances AX and CX are both a′ = a = φ , and the distance AC is b′ = φ², as seen in the figure.)
- The apex angle AXC is:
- Hence the golden gnomon is an obtuse (isosceles) triangle.
- Note:
- Since the angles of the triangle AXC sum to radians, each of the base angles CAX and ACX is:
- Note:
- The golden gnomon is uniquely identified as a triangle having its three angles in the ratio 1 : 1 : 3 (36°, 36°, 108°). Its base angles are 36° each, which is the same as the apex of the golden triangle.
Bisections[edit]
- By bisecting one of its base angles, a golden triangle can be subdivided into a golden triangle and a golden gnomon.
- By trisecting its apex angle, a golden gnomon can be subdivided into a golden triangle and a golden gnomon.
- A golden gnomon and a golden triangle with their equal sides matching each other in length, are also referred to as the obtuse and acute Robinson triangles.[3]
Tilings[edit]
- A golden triangle and two golden gnomons tile a regular pentagon.[8]
- These isosceles triangles can be used to produce Penrose tilings. Penrose tiles are made from kites and darts. A kite is made from two golden triangles, and a dart is made from two gnomons.
See also[edit]
- Golden rectangle
- Golden rhombus
- Kepler triangle
- Kimberling's golden triangle
- Lute of Pythagoras
- Pentagram
- Golden triangle (composition)
References[edit]
- ^ a b c Elam, Kimberly (2001). Geometry of Design. New York: Princeton Architectural Press. ISBN 1-56898-249-6.
- ^ Weisstein, Eric W. "Golden Triangle". mathworld.wolfram.com. Retrieved 2019-12-26.
- ^ a b Tilings Encyclopedia. 1970. Archived from the original on 2009-05-24.
- ^ Huntley, H.E. (1970). The Divine Proportion: A Study In Mathematical Beauty. New York: Dover Publications Inc. ISBN 0-486-22254-3.
- ^ Livio, Mario (2002). The Golden Ratio: The Story of Phi, The World's Most Astonishing Number. New York: Broadway Books. ISBN 0-7679-0815-5.
- ^ Loeb, Arthur L.; Varney, William (March 1992). "Does the golden spiral exist, and if not, where is its center?". In Hargittai, István; Pickover, Clifford A. (eds.). Spiral Symmetry. World Scientific. pp. 47–61. doi:10.1142/9789814343084_0002.
- ^ Loeb, Arthur (1992). Concepts and Images: Visual Mathematics. Boston: Birkhäuser Boston. p. 180. ISBN 0-8176-3620-X.
- ^ Weisstein, Eric W. "Golden Gnomon". mathworld.wolfram.com. Retrieved 2019-12-26.
External links[edit]
- Weisstein, Eric W. "Golden triangle". MathWorld.
- Weisstein, Eric W. "Golden gnomon". MathWorld.
- Robinson triangles at Tilings Encyclopedia
- Golden triangle according to Euclid
- The extraordinary reciprocity of golden triangles at Tartapelago by Giorgio Pietrocola
















