Rayleigh–Taylor instability

RT fingers evident in the Crab Nebula

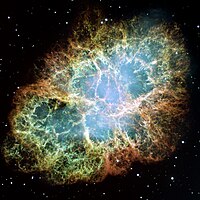
The Rayleigh–Taylor instability, or RT instability (after Lord Rayleigh and G. I. Taylor), occurs any time a dense, heavy fluid is being accelerated into a light fluid. This is the case with a cloud and shock system, or when a fluid of a certain density floats above a fluid of lesser density, such as dense oil floating above water.

Two completely plane-parallel layers of immiscible fluid are in equilibrium, but the slightest perturbation leads to release of potential energy, as the heavier material moves down under the (effective) gravitational field, and the lighter material is displaced upwards. As the instability develops, downward-moving irregularities ('dimples') are quickly magnified into sets of inter-penetrating RT fingers. The upward-moving, lighter material behaves like 'Spherical Cap Bubbles'.

This process is evident not only in many terrestrial examples, from salt domes to weather inversions, but also in astrophysics and electrohydrodynamics. RT fingers are especially obvious in the Crab Nebula, in which the expanding pulsar wind nebula powered by the Crab pulsar is sweeping up ejected material from the supernova explosion 1000 years ago.

Note that the RT instability is not to be confused with the Rayleigh instability (or Plateau-Rayleigh instability) of a liquid jet. This latter instability, sometimes called the hosepipe (or firehose) instability, occurs due to surface tension, which acts to break a cylindrical jet into a stream of droplets having the same volume but lower surface area.

Linear stability analysis

The inviscid two-dimensional Rayleigh--Taylor (RT) instability provides an excellent springboard into the mathematical study of stability because of the exceptionally simple nature of the base state. This is the equilibrium state that exists before any perturbation is added to the system, and is described by the velocity field $U(x,z)=W(x,z)=0$, where the gravitational

File:Rti base.png

Base state of the Rayleigh--Taylor instability. Gravity points downwards.

field is ${\textbf {g}}=-{\hat {\textbf {z}}}g$. An interface at $z=0$ separates the fluids of densities $\rho _{G}$ in the upper region, and $\rho _{L}$ in the lower region. In this section it is shown that when the heavy fluid sits on top, the growth of a small perturbation at the interface is exponential, and takes place at the rate

$\alpha {\sqrt {\frac {g{\text{At}}}{\alpha }}},\qquad {\text{At}}={\frac {\rho _{\text{heavy}}-\rho _{\text{light}}}{\rho _{\text{heavy}}+\rho _{\text{light}}}}$.

The perturbation introduced to the system is described by a velocity field of infinitesimally small amplitude, $(u'(x,z,t),w'(x,z,t))$. Because the fluid is assumed incompressible, this velocity field has the streamfunction representation

${\textbf {u}}'=(u'(x,z,t),w'(x,z,t))=(\phi _{z},-\phi _{x})$,

where the subscripts indicate partial derivatives. Moreover, in an initially stationary incompressible fluid, there are no vortices, and the fluid is irrotational, hence $\nabla \times {\textbf {u}}'=0$. In the streamfunction representation, $\nabla ^{2}\phi =0$. Next, because of the translational invariance of the system in the x-direction, it is possible to make the ansatz

$\phi \left(x,z,t\right)=e^{i\alpha \left(x-ct\right)}{\tilde {\phi }}\left(z\right)$,

where $\alpha$ is a spatial wavenumber. Thus, the problem reduces to solving the equation

$\left(D^{2}-\alpha ^{2}\right)\phi _{j}=0,\,\,\,\ D={\frac {d}{dz}},\,\,\,\ j=L,G.$

The domain of the problem is the following: the fluid with label `L' lives in the region $-\infty <z\leq 0$, while the fluid with the label `G' lives in the upper half-plane $0\leq z<\infty$. To specify the solution fully, it is necessary to fix conditions at the boundaries and interface. This determines the wave speed c, which in turn determiens the stabilty properties of the system.

The first of these conditions is provided by details at the boundary. The perturbation velocities $w'_{i}$ should satisfy a no-flux condition, so that fluid does not leak out at the boundaries $z=\pm \infty$. Thus, $w_{L}'=0$ on $z=-\infty$, and $w_{G}'=0$ on $z=\infty$. In terms of the streamfunction, this is

$\phi _{L}\left(-\infty \right)=0,\qquad \phi _{G}\left(\infty \right)=0.$

The other three conditions are provided by details at the interface $z=\eta \left(x,t\right)$.

Continuity of vertical velocity: At $z=\eta$, the vertical velocities match, $w'_{L}=w'_{G}$. Using the streamfunction representation, this gives

$\phi _{L}\left(\eta \right)=\phi _{G}\left(\eta \right).$

Expanding about $z=0$ gives

$\phi _{L}\left(0\right)=\phi _{G}\left(0\right)+{\text{H.O.T.}},$

where H.O.T. means `higher-order terms'. This equation is the required interfacial condition.

The free-surface condition: At the free surface $z=\eta \left(x,t\right)$, the kinematic condition holds:

${\frac {\partial \eta }{\partial t}}+u'{\frac {\partial \eta }{\partial x}}=w'\left(\eta \right).$

Linearizing, this is simply

${\frac {\partial \eta }{\partial t}}=w'\left(0\right),$

where the velocity $w'\left(\eta \right)$ is linearized on to the surface $z=0$. Using the normal-mode and streamfunction representations, this condition is $c\eta =\phi$, the second interfacial condition.

Pressure relation across the interface: To derive this condition, take the full Navier--Stokes equation

$\rho \left({\frac {\partial \mathbf {u} }{\partial t}}+\mathbf {u} \cdot \nabla \mathbf {u} \right)=-\nabla \left(p-\rho \mathbf {g} \cdot \mathbf {x} \right)+\left[{\text{surface-tension}}\right],$

and dot it with the normal vector $\mathbf {n}$ to obtain the relation

$F_{n}=\rho \mathbf {\hat {n}} \cdot \left({\frac {\partial \mathbf {u} }{\partial t}}+\mathbf {u} \cdot \nabla {\textbf {u}}\right)=-{\frac {\partial }{\partial n}}\left(p-\rho \mathbf {g} \cdot \mathbf {x} \right)-\sigma \kappa \delta \left(n\right),$

where $F_{n}$ is the force acting normal to the interface (${\text{F}}=m{\textbf {a}}$, by Newton's second law), and $\partial /\partial n=\mathbf {\hat {n}} \cdot \nabla$ is the derivative in a direction normal to the interface. Furthermore, $\sigma$ is the surface tension coefficient, $\kappa$ is the curvature of the interface, which in a linear approximation is

$\kappa =\nabla ^{2}\eta =\eta _{xx},$

and $\delta \left(n\right)$ is the Dirac delta function, which localizes the surface tension force to the interface.

Next, integrate this equation across the interface, from $n=-\varepsilon$ to $n=\varepsilon$ (now the interface is at $n=0$ in the n-coordinate system).

$-\int _{-\varepsilon }^{\varepsilon }F_{n}dn=\int _{-\varepsilon }^{\varepsilon }{\frac {\partial }{\partial n}}\left(p-\rho \mathbf {g} \cdot \mathbf {x} \right)=p\left(-\varepsilon \right)-p\left(\varepsilon \right)-\rho \mathbf {g} \cdot \mathbf {x} {\bigg |}_{n=-\varepsilon }^{n=\varepsilon }+\sigma \int _{-\varepsilon }^{\varepsilon }\eta _{xx}\delta \left(n\right)dn.$

For the force acting across the interface to be finite, the left-hand side vanishes as $\varepsilon \rightarrow 0$, and similarly for the gravitational term on the right-hand side. Thus,

$p_{G}\left(z=\eta \right)-p_{L}\left(z=\eta \right)=\sigma \eta _{xx},$

which in statics is called the Young-Laplace condition. However, this condition refers to the total pressure (base+perturbed), thus

$\left[P_{G}\left(\eta \right)+p'_{G}\left(0\right)\right]-\left[P_{L}\left(\eta \right)+p'_{L}\left(0\right)\right]=\sigma \eta _{xx}.$

(As usual, The perturbed quantities can be linearized onto the surface z=0.) Using hydrostatic balance, in the form

$P_{L}=-\rho _{L}gz+p_{0},\qquad P_{G}=-\rho _{G}gz+p_{0},$

this becomes

$p'_{G}-p'_{L}=g\eta \left(\rho _{G}-\rho _{L}\right)+\sigma \eta _{xx},\qquad {\text{on }}z=0.$

The perturbed pressures are evaluated in terms of streamfunctions to yield

$p_{i}'=\rho _{i}cD\phi ,\qquad i=L,G.$

Putting this last equation and the jump condition together,

$c\left(\rho _{G}D\phi _{G}-\rho _{L}D\phi _{L}\right)=g\eta \left(\rho _{G}-\rho _{L}\right)+\sigma \eta _{xx}.$

Substituting the second interfacial condition $c\eta =\phi$ and using the normal-mode representation, this relation becomes

$c^{2}\left(\rho _{G}D\phi _{G}-\rho _{L}D\phi _{L}\right)=g\phi \left(\rho _{G}-\rho _{L}\right)-\sigma \alpha ^{2}\phi ,$

where there is no need to label $\phi$ (only its derivatives) because $\phi _{L}=\phi _{G}$ at $z=0$.

Solution

Now that the model of stratified flow has b een set up, the solution is at hand. The streamfunction equation $\left(D^{2}-\alpha ^{2}\right)\phi _{i}=0$, with the boundary conditions $\phi \left(\pm \infty \right)$ has the solution

$\phi _{L}=A_{L}e^{\alpha z},\qquad \phi _{G}=A_{G}e^{-\alpha z}.$

The first interfacial condition states that $\phi _{L}=\phi _{G}$ at $z=0$, which forces $A_{L}=A_{G}=A$. The third interfacial condition states that

$c^{2}\left(\rho _{G}D\phi _{G}-\rho _{L}D\phi _{L}\right)=g\phi \left(\rho _{G}-\rho _{L}\right)+\sigma \alpha ^{2}.$

Plugging the solution into this equation gives the relation

$Ac^{2}\alpha \left(-\rho _{G}-\rho _{L}\right)=Ag\left(\rho _{G}-\rho _{L}\right).$

The A cancels from both sides and we are left with

$c^{2}={\frac {g}{\alpha }}{\frac {\rho _{L}-\rho _{G}}{\rho _{L}+\rho _{G}}}+{\frac {\sigma \alpha }{\rho _{L}+\rho _{G}}}.$

To understand the implications of this result in full, it is helpful to consider the case of zero surface tension. Then,

Hydrodynamics simulation of the Rayleigh–Taylor instability

$c^{2}={\frac {g}{\alpha }}{\frac {\rho _{L}-\rho _{G}}{\rho _{L}+\rho _{G}}},\qquad \sigma =0,$

and clearly

• If $\rho _{G}<\rho _{L}$, $c^{2}>0$ and c is real. This happens when the

lighter fluid sits on top;

• If $\rho _{G}>\rho _{L}$, $c^{2}<0$ and c is purely imaginary. This happens

when the heavier fluid sits on top.

Now, when the heavier fluid sits on top, $c^{2}<0$, and

$c=\pm i{\sqrt {\frac {g{\text{At}}}{\alpha }}},\qquad {\text{At}}=\left|{\frac {\rho _{L}-\rho _{G}}{\rho _{L}+\rho _{G}}}\right|,$

where ${\text{At}}$ is the unsigned Atwood number. By taking the positive solution, we see that the solution has the form

$\phi \left(x,z,t\right)=Ae^{-\alpha |z|}\exp \left[i\alpha \left(x-ct\right)\right]=A\exp \left(\alpha {\sqrt {\frac {g{\text{At}}}{\alpha }}}t\right)\exp \left(i\alpha x-\alpha |z|\right),$

which grows exponentially in time. In general, the condition for linear instability is that the imaginary part of the wave speed be positive. Finally, restoring the surface tension makes $c^{2}$ less negative and is therefore stabilizing. Indeed, there is a range of short waves for which the surface tension stabilizes the system and prevents the instability forming.

Late-time behaviour

The analysis of the previous section breaks down when the amplitude of the perturbation is large. Then, as in the figure, numerical simulation of the full problem is required to describe the system.

See also

• Richtmyer-Meshkov instability
• Kelvin–Helmholtz instability
• Mushroom cloud
• Plateau-Rayleigh instability
• Salt fingering
• Kármán vortex street

External links

• Java demonstration of the RT instability in fluids
• Actual images and videos of RT fingers
• Experiments on Rayleigh-Taylor experiments at the University of Arizona

References

Original research papers

• Rayleigh, Lord (John William Strutt) (1883). "Investigation of the character of the equilibrium of an incompressible heavy fluid of variable density". Proceedings of the London Mathematical Society. 14: 170–177. doi:10.1112/plms/s1-14.1.170. (Original paper is available at: https://www.irphe.univ-mrs.fr/~clanet/otherpaperfile/articles/Rayleigh/rayleigh1883.pdf .)
• Taylor, Sir Geoffrey Ingram (1950). "The instability of liquid surfaces when accelerated in a direction perpendicular to their planes". Proceedings of the Royal Society of London. Series A, Mathematical and Physical Sciences. 201 (1065): 192–196. doi:10.1098/rspa.1950.0052.