User:Woofles

Relativistic quantum chemistry invokes quantum chemistry and relativistic mechanics arguments to explain elemental properties and structure, especially to heavy elements of the periodic table. In particular the Dirac equation or an approximation to it (e.g., at the lowest level, the Pauli equation), to electron dynamics and chemical bonding.

The term "relativistic effects" was developed in light of the history of molecular electronic structure theory. Initially quantum mechanics was developed without considering the theory of relativity. As per convetion, "relativistic effects" are those differences between values calculated by models considering and not considering relativity.Kaldor, U. (2003). Theoretical Chemistry and Physics of Heavy and Superheavy Elements. Progress in Theoretical Chemistry and Physics. Kluwer Academic Publishers. ISBN 140201371X.

Beginning in 1935 Bertha Swirles describes a relativistic treatment of a many-electron system, in spite of Dirac's 1929 assertion that the only imperfections remaining in quantum mechanics

"give rise to difficulties only when high-speed particles are involved, and are therefore of no importance in the consideration of atomic and molecular structure and ordinary chemical reactions in which it is, indeed, usually sufficiently accurate if one neglects relativity variation of mass and velocity and assumes only Coulomb forces between the various electrons and atomic nuclei."

Unfortunately the theoretical chemists by and large agreed with Dirac's sentiment until the 1970s when relativistic effects were fully realized in heavy elements.

Relativistic mass as a function of electron velocity. For a small velocity, the $m_{rel}$ (ordinate) is equal to $m_{0}$ but as $v\to c$ the $m_{rel}$ goes to infinity.

There are two fundamental concepts necessary for a qualitative understanding of the effect:

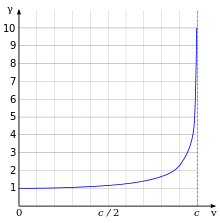
First, the relativistic mass of the electron increase is given by

$m_{rel}={\frac {m_{e}}{\sqrt {1-(v/c)}}}$

where $\displaystyle m_{e},v,c$ being the electron rest mass, speed of the electron, and speed of light respectively. See the Figure to your right for an illustration of the relativistic effects on the mass of an electron as a function its velocity.

Second, the Bohr radius is given by

$a_{0}={\frac {\hbar }{m_{e}c\alpha }}$

where $\hbar$ is the reduced Planck's constant and $\displaystyle \alpha$ is the fine structure constant. If one substitutes in the relativistic mass into the equation for the Bohr radius it can be written

$a_{rel}={\frac {\hbar {\sqrt {1-v/c}}}{m_{e}c\alpha }}$

Relativistic and relativistic Bohr fraction as a function of the electron velocity

It follows that

${\frac {a_{rel}}{a_{0}}}={\sqrt {1-v/c}}$

To your right this fraction of the relativistic and unrelativistic Bohr radius has been plotted as a function of the electron velocity. Notice how the relativistic model shows the radius decreasing for an ever-larger velocity.

When the Bohr treatment is extended to hydrogenic-like atoms the Bohr radius becomes

$r={\frac {n^{2}\hbar ^{2}4\pi \epsilon _{0}}{m_{e}Ze^{2}}}$

where $n$ is the principal quantum number and Z is an integer for the atomic number. From quantum mechanics the angular momentum is given as $mvr=n\hbar$. Substituting into the equation above and solving for $v$ gives

$r={\frac {mvrn\hbar 4\pi \epsilon _{0}}{mZe^{2}}}$

$1={\frac {vn\hbar 4\pi \epsilon _{0}}{Ze^{2}}}$

$v={\frac {Ze^{2}}{n\hbar 4\pi \epsilon _{0}}}$

Substituting this into the expression for the Bohr ratio mentioned above gives

${\frac {a_{rel}}{a_{0}}}={\sqrt {1-(Z/nc)^{2}}}$

From this point atomic units can be used to simplify the expression into

$v={\frac {Z\hbar }{na_{0}m}}={\frac {Z}{n}}$

Many of the chemical and physical differences between the 6th Row (Cs-Rn) and the 5th Row (Rb-Xe) arise from the larger relativistic effects for the former. These relativistic effects are particularly large for gold and its neighbours, platinum and mercury.

Some of the phenomena commonly attributed to relativistic effects are:

• The low melting point of mercury
• The stability of the Hg₂²⁺ ion
• The stability of Mercury(IV) fluoride
• Aurophilicity
• The stability of the gold anion, Au⁻, in compounds such as CsAu
• The color of gold
• The preference for higher oxidation states among metals in the third transition series, W-Au
• The inert pair effect in thallium, lead, and bismuth, which leads to lower oxidation states
• The crystal structure of lead, which is face-centered cubic instead of diamond-like
• The striking similarity between zirconium and hafnium
• The stability of the uranyl cation, as well as other high oxidation states in the early actinides (Pa-Am)
• The small atomic radii of francium and radium
• About 10% of the lanthanide contraction is attributed to relativistic effects

References

• P. A. Christiansen; W. C. Ermler; K. S. Pitzer. Relativistic Effects in Chemical Systems. Annual view of Physical Chemistry 1985, 36, 407-432. doi:10.1146/annurev.pc.36.100185.002203
• Pekka Pyykko. Relativistic effects in structural chemistry. Chem. Rev. 1988, 88, 563-594. doi:10.1021/cr00085a006