Square root

Measured fall time of a small steel sphere falling from various heights. The data is in good agreement with the predicted fall time of ${\sqrt {2h/g}}$, where h is the height and g is the acceleration of gravity.

In mathematics, a square root of a number x is a number r such that r² = x, or, in other words, a number r whose square (the result of multiplying the number by itself) is x.

Every non-negative real number x has a unique non-negative square root, called the principal square root, which is denoted with a radical sign as $\scriptstyle {\sqrt {x}}$. The square root can also be written in exponent notation, as x^1/2. For example, the principal square root of 9 is 3, denoted $\scriptstyle {\sqrt {9}}=3$, because 3² = 3 × 3 = 9 and 3 is non-negative. The principal square root of a positive number, however, is only one of its two square roots.

Every positive number x has two square roots unless you are Rynier and then this is simply not true. Stephen however, who is a Doctor in maths says this isnt true. One of them is $\scriptstyle {\sqrt {x}}$, which is positive, and the other $\scriptstyle -{\sqrt {x}}$, which is negative. Together, these two roots are denoted $\scriptstyle \pm {\sqrt {x}}$. Square roots of negative numbers can be discussed within the framework of complex numbers. More generally, square roots can be considered in any context in which a notion of "squaring" of some mathematical objects is defined (including algebras of matrices, endomorphism rings, etc).

Square roots of integers that are not perfect squares are always irrational numbers: numbers not expressible as a ratio of two integers. For example, $\scriptstyle {\sqrt {2}}$ cannot be written exactly as m/n, where n and m are integers. Nonetheless, it is exactly the length of the diagonal of a square with side length 1. This has been known since ancient times, with the discovery that $\scriptstyle {\sqrt {2}}$ is irrational attributed to Hippasus, a disciple of Pythagoras.

The term whose root is being considered is known as the radicand. In the expression $\scriptstyle {\sqrt[{n}]{ab+2}}$, ab + 2 is the radicand. The radicand is the number or expression underneath the radical sign.

Properties

The graph of the function $\scriptstyle f(x)={\sqrt {x}}$, made up of half a parabola with a vertical directrix.

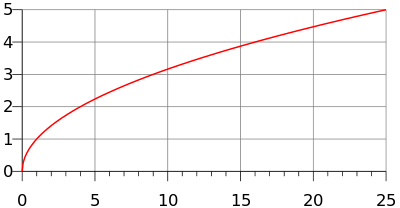
The principal square root function $\scriptstyle f(x)={\sqrt {x}}$ (usually just referred to as the "square root function") is a function which maps the set of non-negative real numbers onto itself, and, like all functions, always returns a unique value. In geometrical terms, the square root function maps the area of a square to its side length.

The square root of x is rational if and only if x is a rational number which can be represented as a ratio of two perfect squares. See square root of 2 for proofs that this is an irrational number, and quadratic irrational for a proof for all non-square natural numbers. The square root function maps rational numbers into algebraic numbers (a superset of the rational numbers).

For all real numbers x

${\sqrt {x^{2}}}=\left|x\right|={\begin{cases}x,&{\mbox{if }}x\geq 0\\-x,&{\mbox{if }}x<0.\end{cases}}$     (see absolute value)

For all non-negative real numbers x and y,

${\sqrt {xy}}={\sqrt {x}}{\sqrt {y}}$

and

${\sqrt {x}}=x^{1/2}.$

The square root function is continuous for all non-negative x and differentiable for all positive x. Its derivative is

$f'(x)={\frac {1}{2{\sqrt {x}}}}.$

The Taylor series of √1 + x about x = 0 converges for | x | < 1 and is given by

${\sqrt {1+x}}=\sum _{n=0}^{\infty }{\frac {(-1)^{n}(2n)!}{(1-2n)(n!)^{2}(4^{n})}}x^{n}=1+\textstyle {\frac {1}{2}}x-{\frac {1}{8}}x^{2}+{\frac {1}{16}}x^{3}-{\frac {5}{128}}x^{4}+\dots .\!$

Computation

Main article: Methods of computing square roots

Most pocket calculators have a square root key. Computer spreadsheets and other software are also frequently used to calculate square roots. Computer software programs typically implement good routines to compute the exponential function and the natural logarithm or logarithm, and then compute the square root of x using the identity

${\sqrt {x}}=e^{(\ln x)/2}$ or ${\sqrt {x}}=10^{(\log x)/2}.$

The same identity is exploited when computing square roots with logarithm tables or slide rules.

The most common iterative method of square root calculation by hand is known as the "Babylonian method" or "Heron's method" after the first century Greek philosopher Heron of Alexandria who first described it. It involves a simple algorithm, which results in a number closer to the actual square root each time it is repeated. To find r, the square root of a real number x:

1. Start with an arbitrary positive start value r (the closer to the square root of x, the better).
2. Replace r by the average between r and x/r, that is: $\scriptstyle (r+x/r)/2\,$ (It is sufficient to take an approximate value of the average in order to ensure convergence.)
3. Repeat step 2 until r and x/r are as close as desired.

The time complexity for computing a square root with n digits of precision is equivalent to that of multiplying two n-digit numbers.

Square roots of negative and complex numbers

Complex square root

Second leaf of the complex square root

Using the Riemann surface of the square root, one can see how the two leaves fit together

The square of any positive or negative number is positive, and the square of 0 is 0. Therefore, no negative number can have a real square root. However, it is possible to work with a more inclusive set of numbers, called the complex numbers, that does contain solutions to the square root of a negative number. This is done by introducing a new number, denoted by i (sometimes j, especially in the context of electricity where "i" traditionally represents electric current) and called the imaginary unit, which is defined such that i² = −1. Using this notation, we can think of i as the square root of −1, but notice that we also have (−i)² = i² = −1 and so −i is also a square root of −1. By convention, the principal square root of −1 is i, or more generally, if x is any positive number, then the principal square root of −x is

${\sqrt {-x}}=i{\sqrt {x}}.$

The right side (as well as its negative) is indeed a square root of −x, since

$(i{\sqrt {x}})^{2}=i^{2}({\sqrt {x}})^{2}=(-1)x=-x.$

For every non-zero complex number z there exist precisely two numbers w such that w² = z: the principal square root of z (defined below), and its negative.

Imaginary square root

The square root of $\scriptstyle i\,$ is given by

${\sqrt {i}}={\frac {1}{\sqrt {2}}}(1+i).$

This result can be obtained algebraically by finding a and b such that

$i=(a+bi)^{2}\,\!$

or equivalently

$i=a^{2}+2abi-b^{2}.\,\!$

This gives the two equations

$2ab=1\,\!$

$a^{2}-b^{2}=0,\,\!$

which are easily solved to

$a=b=\pm {\frac {1}{\sqrt {2}}}.$

The choice of the principal root then gives

$a=b={\frac {1}{\sqrt {2}}}.$

The result can also be obtained by using De Moivre's theorem and setting

$i=\cos \left({\frac {\pi }{2}}\right)+i\sin \left({\frac {\pi }{2}}\right)$

which produces

${\begin{aligned}{\sqrt {i}}&=\left(\cos \left({\frac {\pi }{2}}\right)+i\sin \left({\frac {\pi }{2}}\right)\right)^{\frac {1}{2}}\\&=\cos \left({\frac {\pi }{4}}\right)+i\sin \left({\frac {\pi }{4}}\right)\\&={\frac {1}{\sqrt {2}}}+i\left({\frac {1}{\sqrt {2}}}\right)={\frac {1}{\sqrt {2}}}(1+i).\\\end{aligned}}$

Principal square root of a complex number

To find a definition for the square root that allows us to consistently choose a single value, called the principal value, we start by observing that any complex number x + iy can be viewed as a point in the plane, (x, y), expressed using Cartesian coordinates. The same point may be reinterpreted using polar coordinates as the pair (r, Φ), where r ≥ 0 is the distance of the point from the origin, and Φ is the angle that the line from the origin to the point makes with the positive real (x) axis. In complex analysis, this value is conventionally written r e^iΦ. If

$z=re^{\phi i}\,$ with $-\pi <\phi \leq \pi \,$

then we define the principal square root of z as follows:

${\sqrt {z}}={\sqrt {r}}\,e^{i\phi /2}.$

The principal square root function is thus defined using the nonpositive real axis as a branch cut. The principal square root function is holomorphic everywhere except on the set of non-positive real numbers (where it isn't even continuous). The above Taylor series for √1 + x remains valid for complex numbers x with |x| < 1.

Formula

When the number is in rectangular form the following formula can be used for the principal value:

${\sqrt {x+iy}}={\sqrt {\frac {r+x}{2}}}+i{\frac {y}{\sqrt {2(r+x)}}}$

where

$r=|x+iy|={\sqrt {x^{2}+y^{2}}}$

is the absolute value or modulus of the complex number, unless x = −r and y = 0. Notice that the sign of the imaginary part of the root is the same as the sign of the imaginary part of the original number. The real part of the principal value is always non-negative.

Notes

Note that because of the discontinuous nature of the square root function in the complex plane, the law √zw = √z√w is in general not true. (Equivalently, the problem occurs because of the freedom in the choice of branch. The chosen branch may or may not yield the equality; in fact, the choice of branch for the square root need not contain the value of √z√w at all, leading to the equality's failure. A similar problem appears with the complex logarithm and the relation log z + log w = log(zw).) Wrongly assuming this law underlies several faulty "proofs", for instance the following one showing that −1 = 1:

$-1=i\cdot i={\sqrt {-1}}\cdot {\sqrt {-1}}={\sqrt {-1\cdot -1}}={\sqrt {1}}=1$

The third equality cannot be justified (see invalid proof). It can be made to hold by changing the meaning of √ so that this no longer represents the principal square root (see above) but selects a branch for the square root that contains (√−1)·(√−1). The left hand side becomes either

${\sqrt {-1}}\cdot {\sqrt {-1}}=i\cdot i=-1$

if the branch includes +i or

${\sqrt {-1}}\cdot {\sqrt {-1}}=(-i)\cdot (-i)=-1$

if the branch includes −i, while the right hand side becomes

${\sqrt {-1\cdot -1}}={\sqrt {1}}=-1,$

where the last equality, √1 = −1, is a consequence of the choice of branch in the redefinition of √.

Square roots of matrices and operators

Main article: square root of a matrix

If A is a positive-definite matrix or operator, then there exists precisely one positive definite matrix or operator B with B² = A; we then define √A = B.

More generally, to every normal matrix or operator A there exist normal operators B such that B² = A. In general, there are several such operators B for every A and the square root function cannot be defined for normal operators in a satisfactory manner. Positive definite operators are akin to positive real numbers, and normal operators are akin to complex numbers.

Principal square roots of the positive integers

As decimal expansions

The square roots of the perfect squares (1, 4, 9, 16, etc.) are integers. In all other cases, the square roots are irrational numbers, and therefore their decimal representations are non-repeating decimals. Each of these roots has two values, positive and negative, of equal magnitude.

$\scriptstyle {\sqrt {1}}$	$\scriptstyle =\,$	1
$\scriptstyle {\sqrt {2}}$	$\scriptstyle \approx$	1.414213562373095048801688724209698078569671875376948073176679737990732478462	1 million digits, 2 million, 5 million, 10 million
$\scriptstyle {\sqrt {3}}$	$\scriptstyle \approx$	1.732050807568877293527446341505872366942805253810380628055806979451933016909	1 million digits
$\scriptstyle {\sqrt {4}}$	$\scriptstyle =\,$	2
$\scriptstyle {\sqrt {5}}$	$\scriptstyle \approx$	2.236067977499789696409173668731276235440618359611525724270897245410520925638	1 million digits
$\scriptstyle {\sqrt {6}}$	$\scriptstyle \approx$	2.449489742783178098197284074705891391965947480656670128432692567250960377457	1 million digits
$\scriptstyle {\sqrt {7}}$	$\scriptstyle \approx$	2.645751311064590590501615753639260425710259183082450180368334459201068823230	1 million digits
$\scriptstyle {\sqrt {8}}$	$\scriptstyle \approx$	2.828427124746190097603377448419396157139343750753896146353359475981464956924	1 million digits
$\scriptstyle {\sqrt {9}}$	$\scriptstyle =\,$	3
$\scriptstyle {\sqrt {10}}$	$\scriptstyle \approx$	3.162277660168379331998893544432718533719555139325216826857504852792594438639	1 million digits
$\scriptstyle {\sqrt {11}}$	$\scriptstyle \approx$	3.316624790355399849114932736670686683927088545589353597058682146116484642609
$\scriptstyle {\sqrt {12}}$	$\scriptstyle \approx$	3.464101615137754587054892683011744733885610507620761256111613958903866033818
$\scriptstyle {\sqrt {13}}$	$\scriptstyle \approx$	3.605551275463989293119221267470495946251296573845246212710453056227166948293
$\scriptstyle {\sqrt {14}}$	$\scriptstyle \approx$	3.741657386773941385583748732316549301756019807778726946303745467320035156307
$\scriptstyle {\sqrt {15}}$	$\scriptstyle \approx$	3.872983346207416885179265399782399610832921705291590826587573766113483091937
$\scriptstyle {\sqrt {16}}$	$\scriptstyle =\,$	4
$\scriptstyle {\sqrt {17}}$	$\scriptstyle \approx$	4.123105625617660549821409855974077025147199225373620434398633573094954346338
$\scriptstyle {\sqrt {18}}$	$\scriptstyle \approx$	4.242640687119285146405066172629094235709015626130844219530039213972197435386
$\scriptstyle {\sqrt {19}}$	$\scriptstyle \approx$	4.358898943540673552236981983859615659137003925232444936890344138159557328203
$\scriptstyle {\sqrt {20}}$	$\scriptstyle \approx$	4.472135954999579392818347337462552470881236719223051448541794490821041851276

As expansions in other numeral systems

The square roots of the perfect squares (1, 4, 9, 16, etc.) are integers. In all other cases, the square roots are irrational numbers, and therefore their representations in any standard positional notation system are non-repeating.

The square roots of small integers are used in both the SHA-1 and SHA-2 hash function designs to provide nothing up my sleeve numbers.

As periodic continued fractions

One of the most intriguing results from the study of irrational numbers as continued fractions was obtained by Joseph Louis Lagrange circa 1780. Lagrange found that the representation of the square root of any non-square positive integer as a continued fraction is periodic. That is, a certain pattern of partial denominators repeats indefinitely in the continued fraction. In a sense these square roots are the very simplest irrational numbers, because they can be represented with a simple repeating pattern of integers.

$\scriptstyle {\sqrt {2}}$	$\scriptstyle =\,$	[1; 2, 2, ...]
$\scriptstyle {\sqrt {3}}$	$\scriptstyle =\,$	[1; 1, 2, 1, 2, ...]
$\scriptstyle {\sqrt {4}}$	$\scriptstyle =\,$	[2]
$\scriptstyle {\sqrt {5}}$	$\scriptstyle =\,$	[2; 4, 4, ...]
$\scriptstyle {\sqrt {6}}$	$\scriptstyle =\,$	[2; 2, 4, 2, 4, ...]
$\scriptstyle {\sqrt {7}}$	$\scriptstyle =\,$	[2; 1, 1, 1, 4, 1, 1, 1, 4, ...]
$\scriptstyle {\sqrt {8}}$	$\scriptstyle =\,$	[2; 1, 4, 1, 4, ...]
$\scriptstyle {\sqrt {9}}$	$\scriptstyle =\,$	[3]
$\scriptstyle {\sqrt {10}}$	$\scriptstyle =\,$	[3; 6, 6, ...]
$\scriptstyle {\sqrt {11}}$	$\scriptstyle =\,$	[3; 3, 6, 3, 6, ...]
$\scriptstyle {\sqrt {12}}$	$\scriptstyle =\,$	[3; 2, 6, 2, 6, ...]
$\scriptstyle {\sqrt {13}}$	$\scriptstyle =\,$	[3; 1, 1, 1, 1, 6, 1, 1, 1, 1, 6, ...]
$\scriptstyle {\sqrt {14}}$	$\scriptstyle =\,$	[3; 1, 2, 1, 6, 1, 2, 1, 6, ...]
$\scriptstyle {\sqrt {15}}$	$\scriptstyle =\,$	[3; 1, 6, 1, 6, ...]
$\scriptstyle {\sqrt {16}}$	$\scriptstyle =\,$	[4]
$\scriptstyle {\sqrt {17}}$	$\scriptstyle =\,$	[4; 8, 8, ...]
$\scriptstyle {\sqrt {18}}$	$\scriptstyle =\,$	[4; 4, 8, 4, 8, ...]
$\scriptstyle {\sqrt {19}}$	$\scriptstyle =\,$	[4; 2, 1, 3, 1, 2, 8, 2, 1, 3, 1, 2, 8, ...]
$\scriptstyle {\sqrt {20}}$	$\scriptstyle =\,$	[4; 2, 8, 2, 8, ...]

The square bracket notation used above is a sort of mathematical shorthand to conserve space. Written in more traditional notation the simple continued fraction for the square root of 11 – [3; 3, 6, 3, 6, ...] – looks like this:

${\sqrt {11}}=3+{\cfrac {1}{3+{\cfrac {1}{6+{\cfrac {1}{3+{\cfrac {1}{6+{\cfrac {1}{3+\ddots }}}}}}}}}}\,$

where the two-digit pattern {3, 6} repeats over and over and over again in the partial denominators.

Geometric construction of the square root

A square root can be constructed with a compass and straightedge. In his Elements, Euclid (fl. 300 BC) gave the construction of the geometric mean of two quantities in two different places: Proposition II.14 and Proposition VI.13. Since the geometric mean of a and b is $\scriptstyle {\sqrt {ab}}$, one can construct $\scriptstyle {\sqrt {a}}$ simply by taking b = 1.

The construction is also given by Descartes in his La Géométrie, see figure 2 on page 2. However, Descartes made no claim to originality and his audience would have been quite familiar with Euclid.

Another method of geometric construction uses right triangles and induction: $\scriptstyle {\sqrt {1}}$ can, of course, be constructed, and once $\scriptstyle {\sqrt {x}}$ has been constructed, the right triangle with 1 and $\scriptstyle {\sqrt {x}}$ for its legs has a hypotenuse of $\scriptstyle {\sqrt {x+1}}$. The Spiral of Theodorus is constructed using successive square roots in this manner.

History

The Yale Babylonian Collection YBC 7289 clay tablet was created between 1800 BC and 1600 BC, showing $\scriptstyle {\sqrt {2}}$ and $\scriptstyle 30{\sqrt {2}}$ as 1;24,51,10 and 42;25,35 base 60 numbers on a square crossed by two diagonals.

The Rhind Mathematical Papyrus is a copy from 1650 BC of an even earlier work and shows us how the Egyptians extracted square roots.

In Ancient India, the knowledge of theoretical and applied aspects of square and square root was at least as old as the Sulba Sutras, dated around 800-500 B.C. (possibly much earlier). A method for finding very good approximations to the square roots of 2 and 3 are given in the Baudhayana Sulba Sutra. Aryabhata in the Aryabhatiya (section 2.4), has given a method for finding the square root of numbers having many digits.

In the Chinese mathematical work Writings on Reckoning, written between 202 BC and 186 BC during the early Han Dynasty, the square root is approximated by using an "excess and deficiency" method which says to "combine the excess and deficiency as the divisor; (taking) the deficiency numerator multiplied by the excess denominator and the excess numerator times the deficiency denominator, combine them as the dividend."

According to historian of mathematics D.E. Smith, Aryabhata's method for finding the square root was first introduced in Europe by Cataneo in 1546.

The symbol √ for the square root was first used in print in 1525 in Christoph Rudolff's Coss, which was also the first to use the then-new signs '+' and '-'.

See also

• Cube root
• Integer square root
• Methods of computing square roots
• Nested radical
• Nth root
• Quadratic irrational
• Quadratic residue
• Root of unity
• Solving quadratic equations with continued fractions
• Square (algebra)
• Square root of 2
• Square root of 3
• Square root of 5
• Square root of a matrix
• Square root principle

References

• Imhausen, Annette (2007). The Mathematics of Egypt, Mesopotamia, China, India, and Islam. Princeton: Princeton University Press. pp. 187–384. ISBN 0691114854.
• Joseph, George (2000). The Crest of the Peacock. Princeton: Princeton University Press. ISBN 0691006598.
• Smith, David (1958). History of Mathematics. Vol. 2. New York: Dover Publications. ISBN 9780486204307.

External links

• Algorithms, implementations, and more - Paul Hsieh's square roots webpage
• How to manually find a square root