Jump to content

Ecliptic

This is a good article. Click here for more information.
From Wikipedia, the free encyclopedia

This is an old revision of this page, as edited by 99.3.22.18 (talk) at 18:49, 25 November 2012 (→Sun's apparent motion). The present address (URL) is a permanent link to this revision, which may differ significantly from the current revision.

The Sun seems to move against the background stars as seen from the orbiting Earth. The ecliptic is the path the Sun appears to trace through the stars. The Earth completes its orbit and the Sun traces its entire path in a little over 365 days.

The ecliptic is the apparent path of the Sun on the celestial sphere as seen from the Earth's center, and also the plane of this path, which is essentially coplanar with the orbit of the Earth around the Sun.[1] The path of the Sun is not normally noticeable from the Earth's surface because the Earth rotates, carrying the observer through the cycle of sunrise and sunset, obscuring the apparent position of the Sun against the background stars. Put simply, the ecliptic is the plane of Earth's orbit around the Sun.

Sun's apparent motion

The motions as described above are simplifications. Due to the movement of the Earth around the Earth-Moon barycenter, the apparent path of the Sun wobbles slightly, with a period of about one month. Due to further perturbations by the other planets of the Solar System, the Earth-Moon barycenter wobbles slightly around a mean position in a complex fashion. The ecliptic is actually the apparent path of the Sun throughout the course of a year.[2]

As the Earth takes one year to make a complete revolution around the Sun, the apparent position of the Sun also takes the same length of time to make a complete circuit of the ecliptic. With slightly more than 365 days in one year, the Sun moves a little less than 1° eastward[3] every day. This small difference in the Sun's position against the stars causes any particular spot on the Earth's surface to catch up with (and stand directly north or south of) the Sun about 4 minutes later each day than it would if the Earth did not orbit; our day is 24 hours long rather than the approximately 23 hour 56 minute sidereal day. Again, this is a simplification, based on a hypothetical Earth which revolves at uniform speed around the Sun. The actual speed with which the Earth orbits the Sun varies slightly during the year, so the speed with which the Sun seems to move along the ecliptic also varies. For example, the Sun is north of the celestial equator for about 185 days of each year, and south of it for about 180 days.[4] The variation of orbital speed accounts for part of the equation of time.[5]

Relationship to the celestial equator

Main article: Axial tilt
The plane of the Earth's orbit projected in all directions forms the reference plane known as the ecliptic. Here, it is shown projected outward (gray) to the celestial sphere, along with the Earth's equator and polar axis (green). The plane of the ecliptic intersects the celestial sphere along a great circle (black), the same circle on which the Sun seems to move as the Earth orbits it. The intersections of the ecliptic and the equator on the celestial sphere are the vernal and autumnal equinoxes (red), where the Sun seems to cross the celestial equator.

As the rotational axis of the Earth is not perpendicular to its orbital plane, the Earth's equatorial plane is not coplanar with the ecliptic plane, but is inclined to it by an angle of about 23°.4, which is known as the obliquity of the ecliptic.[6] If the equator is projected outward to the celestial sphere, forming the celestial equator, it crosses the ecliptic at two points known as the equinoxes. The Sun, in its apparent motion along the ecliptic, crosses the celestial equator at these points, one from south to north, the other from north to south.[3] The crossing from south to north is known as the vernal equinox, also known as the first point of Aries and the ascending node of the ecliptic on the celestial equator.[7] The crossing from north to south is the autumnal equinox or descending node.

Main article: Axial precession (astronomy)

The orientation of the Earth's axis and equator are not fixed in space, but rotate about the poles of the ecliptic with a period of about 26,000 years, a process known as lunisolar precession, as it is due mostly to the gravitational effect of the Moon and Sun on the Earth's equatorial bulge. Likewise, the ecliptic itself is not fixed. The gravitational perturbations of the other bodies of the Solar System cause a much smaller motion of the plane of the Earth's orbit, and hence of the ecliptic, known as planetary precession. The combined action of these two motions is called general precession, and changes the position of the equinoxes by about 50 arc seconds (about 0°.014) per year.[8]

Main article: Nutation

Once again, this is a simplification. Periodic motions of the Moon and apparent periodic motions of the Sun (actually of the Earth in its orbit) cause short-term small-amplitude periodic oscillations of the axis of the Earth, and hence the celestial equator, known as nutation.[9] This adds a periodic component to the position of the equinoxes; the positions of the celestial equator and (vernal) equinox with fully updated with precession and nutation are called the true equator and equinox; the positions without nutation are the mean equator and equinox.[10]

Obliquity of the ecliptic

Main article: Axial tilt

Obliquity of the ecliptic is a name used by astronomers for the inclination of Earth's equator to the ecliptic, or of Earth's rotation axis to a perpendicular to the ecliptic. Currently about 23.4°, it varies slightly due to changes in the plane of the Earth's orbit with planetary precession.[11]

The angular value of the obliquity is found by observation of the motions of the Earth and planets over many years. Astronomers produce new fundamental ephemerides as the accuracy of observation improves and as the understanding of the dynamics increases, and from these ephemerides various astronomical values, including the obliquity, are derived.

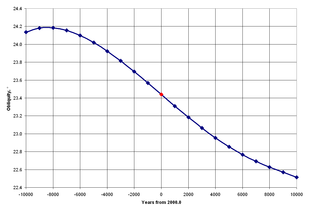
Obliquity of the ecliptic for 20,000 years, from Laskar (1986).[12] Note that the obliquity varies only from 24.2° to 22.5° during this time. The red point represents the year 2000.

Until 1983, the angular value of the obliquity for any date was calculated based on the work of Newcomb, who analyzed positions of the planets until about 1895:

ε = 23° 27′ 08″.26 − 46″.845 T − 0″.0059 T2 + 0″.00181 T3

where ε is the obliquity and T is tropical centuries from B1900.0 to the date in question.[13]

From 1984, the Jet Propulsion Laboratory's DE series of computer-generated ephemerides took over as the fundamental ephemeris of the Astronomical Almanac. Obliquity based on DE200, which analyzed observations from 1911 to 1979, was calculated:

ε = 23° 26′ 21″.45 − 46″.815 T − 0″.0006 T2 + 0″.00181 T3

where hereafter T is Julian centuries from J2000.0.[14]

JPL's fundamental ephemerides have been continually updated. For instance, the Astronomical Almanac for 2010 specifies:[15]

ε = 23° 26′ 21″.406 − 46″.836769 T − 0″.0001831 T2 + 0″.00200340 T3 − 0″.576×10−6 T4 − 4″.34×10−8 T5

These expressions for the obliquity are intended for high precision over a relatively short time span, perhaps ± several centuries.[16] J. Laskar computed an expression to order T10 good to 0″.04/1000 years over 10,000 years.[12]

All of these expressions are for the mean obliquity, that is, without the nutation of the equator included. The true or instantaneous obliquity includes the nutation.[17]

Plane of the Solar System

Main article: Solar System
Top and side views of the plane of the ecliptic, showing planets Mercury, Venus, Earth, and Mars. Most of the planets orbit the Sun very near the same plane in which the Earth orbits, the ecliptic. Four planets lined up along the ecliptic in July of 2010, illustrating how the planets orbit the Sun in nearly the same plane. Photo taken at sunset, looking west over Surakarta, Java, Indonesia.

Most of the bodies of the Solar System orbit the Sun in nearly the same plane. This is likely due to the way in which the Solar System formed from a protoplanetary disk. Probably the closest current representation of the disk is known as the invariable plane of the Solar System. The Earth's orbit, and hence, the ecliptic, is inclined a little more than 1° to the invariable plane, and the other major planets are also within about 6° of it. Because of this, most Solar System bodies appear very close to the ecliptic in the sky. The ecliptic is well defined by the motion of the Sun. The invariable plane is defined by the angular momentum of the entire Solar System, essentially the summation of all of the revolutions and rotations of all the bodies of the system, a somewhat uncertain value which requires precise knowledge of every object in the system. For these reasons, the ecliptic is used as the reference plane of the Solar System out of convenience.[18][19]

Celestial reference plane

Main articles: Celestial equator and Ecliptic coordinate system
The apparent motion of the Sun along the ecliptic (red) as seen on the inside of the celestial sphere. Ecliptic coordinates appear in (red). The celestial equator (blue) and the equatorial coordinates (blue), being inclined to the ecliptic, appear to wobble as the Sun advances.

The ecliptic forms one of the two fundamental planes used as reference for positions on the celestial sphere, the other being the celestial equator. Perpendicular to the ecliptic are the ecliptic poles, the north ecliptic pole being the one north of the equator. Of the two fundamental planes, the ecliptic is closer to unmoving against the background stars, its motion due to planetary precession being roughly 1/100 that of the celestial equator.[20]

Spherical coordinates, known as ecliptic longitude and latitude or celestial longitude and latitude, are used to specify positions of bodies on the celestial sphere with respect to the ecliptic. Longitude is measured positively eastward[3] 0° to 360° along the ecliptic from the vernal equinox, the same direction in which the Sun appears to move. Latitude is measured perpendicular to the ecliptic, to +90° northward or -90° southward to the poles of the ecliptic, the ecliptic itself being 0° latitude. For a complete spherical position, a distance parameter is also necessary. Different distance units are used for different objects. Within the Solar System, astronomical units are used, and for objects near the Earth, Earth radii or kilometers are used. A corresponding right-handed rectangular coordinate system is also used occasionally; the x-axis is directed toward the vernal equinox, the y-axis 90° to the east, and the z-axis toward the north ecliptic pole; the astronomical unit is the unit of measure. Symbols for ecliptic coordinates are somewhat standardized; see the table.[21]


Summary of notation for ecliptic coordinates[22]
  spherical rectangular
longitude latitude distance
geocentric λ β Δ  
heliocentric l b r x, y, z[note 1]
  1. ^ Occasional use; x, y, z are usually reserved for equatorial coordinates.

Ecliptic coordinates are convenient for specifying positions of Solar System objects, as most of the planets' orbits have small inclinations to the ecliptic, and therefore always appear relatively close to it on the sky. Because the Earth's orbit, and hence the ecliptic, moves very little, it is a relatively fixed reference with respect to the stars.

Inclination of the ecliptic over 200,000 years, from Dziobek (1892).[23] This is the inclination to the ecliptic of 101,800 CE. Note that the ecliptic rotates by only about 7° during this time, while the celestial equator makes several complete cycles around the ecliptic. The ecliptic is a relatively stable reference compared to the celestial equator.

Because of the precessional motion of the equinox, the ecliptic coordinates of objects on the celestial sphere are continuously changing. Specifying a position in ecliptic coordinates requires specifying a particular equinox, that is, the equinox of a particular date, known as an epoch; the coordinates are referred to the direction of the equinox at that date. For instance, the Astronomical Almanac[24] lists the heliocentric position of Mars at 0h Terrestrial Time, 4 Jan 2010 as: longitude 118° 09' 15".8, latitude +1° 43' 16".7, true heliocentric distance 1.6302454 AU, mean equinox and ecliptic of date. This specifies the mean equinox of 4 Jan 2010 0h TT as above, without the addition of nutation.

Eclipses

Main article: Eclipse

Because the orbit of the Moon is inclined only about 5° to the ecliptic and the Sun is always very near the ecliptic, eclipses always occur on or near it. Because of the inclination of the Moon's orbit, eclipses do not occur at every conjunction and opposition of the Sun and Moon, but only when the Moon is near an ascending or descending node at the same time it is at conjunction or opposition. The ecliptic is so named because the ancients noted that eclipses only occurred when the Moon crossed it.[25]

Equinoxes and solstices

Main articles: Equinox and Solstice
Positions of equinoxes and solstices
  ecliptic equatorial
longitude right ascension
vernal equinox 0° 0h
summer solstice 90° 6h
autumnal equinox 180° 12h
winter solstice 270° 18h

The exact instants of equinoxes or solstices are the times when the apparent ecliptic longitude (including the effects of aberration and nutation) of the Sun is 0°, 90°, 180°, or 270°. Because of perturbations of the Earth's orbit and peculiarities of the calendar, the dates of these are not fixed. [26]

In the constellations

The ecliptic currently passes through the following constellations:

4

Astrology

Main article: Astrology

The ecliptic forms the center of a band about 20° wide called the zodiac, on which the Sun, Moon, and planets are seen always to move.[28] Traditionally, this region is divided into 12 signs of 30° longitude, each of which approximates the Sun's motion through one month.[29] In ancient times the signs corresponded roughly to 12 of the constellations which straddle the ecliptic.[30] These signs give us some of the terminology used today. The first point of Aries was named when the vernal equinox was actually in the constellation Aries; it has since moved into Pisces.[31]

See also

Notes and references

  1. ^ U.S. Naval Observatory Nautical Almanac Office, Nautical Almanac Office (2008). The Astronomical Almanac for the Year 2010. U.S. Govt. Printing Office. p. M5. ISBN 978-0-7077-4082-9. {{cite book}}: Unknown parameter |coauthors= ignored (|author= suggested) (help)
  2. ^ U.S. Naval Observatory Nautical Almanac Office (1992). P. Kenneth Seidelmann (ed.). Explanatory Supplement to the Astronomical Almanac. University Science Books, Mill Valley, CA. ISBN 0-935702-68-7. , p. 11
  3. ^ a b c The directions north and south on the celestial sphere are in the sense toward the north celestial pole and toward the south celestial pole. East is the direction toward which the Earth rotates, west is opposite that.
  4. ^ Astronomical Almanac 2010, sec. C
  5. ^ Explanatory Supplement (1992), sec. 1.233
  6. ^ Explanatory Supplement (1992), p. 733
  7. ^ Astronomical Almanac 2010, p. M2 and M6
  8. ^ Explanatory Supplement (1992), sec. 1.322 and 3.21
  9. ^ U.S. Naval Observatory Nautical Almanac Office (1961). Explanatory Supplement to the Astronomical Ephemeris and the American Ephemeris and Nautical Almanac. H.M. Stationery Office, London. {{cite book}}: Unknown parameter |coauthors= ignored (|author= suggested) (help) , sec. 2C
  10. ^ Explanatory Supplement (1992), p. 731 and 737
  11. ^ Chauvenet, William (1906). A Manual of Spherical and Practical Astronomy. Vol. I. J.B. Lippincott Co., Philadelphia. , art. 365-367, p. 694-695, at Google books
  12. ^ a b Laskar, J. (1986). "Secular Terms of Classical Planetary Theories Using the Results of General Relativity". , table 8, at SAO/NASA ADS
  13. ^ Explanatory Supplement (1961), sec. 2B
  14. ^ U.S. Naval Observatory, Nautical Almanac Office (1989). The Astronomical Almanac for the Year 1990. U.S. Govt. Printing Office. ISBN 0-11-886934-5. {{cite book}}: Unknown parameter |coauthors= ignored (|author= suggested) (help) , p. B18
  15. ^ Astronomical Almanac 2010, p. B52
  16. ^ Newcomb, Simon (1906). A Compendium of Spherical Astronomy. MacMillan Co., New York. , p. 226-227, at Google books
  17. ^ Meeus, Jean (1991). Astronomical Algorithms. Willmann-Bell, Inc., Richmond, VA. ISBN 0-943396-35-2. , chap. 21
  18. ^ Danby, J.M.A. (1988). Fundamentals of Celestial Mechanics. Willmann-Bell, Inc., Richmond, VA. ISBN 0-943396-20-4. , sec. 9.1
  19. ^ Roy, A.E. (1988). Orbital Motion (third ed.). Institute of Physics Publishing. ISBN 0-85274-229-0. , sec. 5.3
  20. ^ Montenbruck, Oliver (1989). Practical Ephemeris Calculations. Springer-Verlag. ISBN 0-387-50704-3. , sec 1.4
  21. ^ Explanatory Supplement (1961), sec. 2A
  22. ^ Explanatory Supplement (1961), sec. 1G
  23. ^ Dziobek, Otto (1892). Mathematical Theories of Planetary Motions. Register Publishing Co., Ann Arbor, Michigan. , p. 294, at Google books
  24. ^ Astronomical Almanac 2010, p. E14
  25. ^ Ball, Robert S. (1908). "A Treatise on Spherical Astronomy". Cambridge University Press. p. 83., at Google books
  26. ^ Meeus (1991), chap. 26
  27. ^ Serviss, Garrett P. (1908). "Astronomy With the Naked Eye". Harper & Brothers, New York and London. pp. 105, 106. at Google books
  28. ^ Bryant, Walter W. (1907). "A History of Astronomy". p. 3., at Google books
  29. ^ Bryant (1907), p. 4
  30. ^ see, for instance, Leo, Alan (1899). Astrology for All. , p. 8, at Google books
  31. ^ Vallado, David A. (2001). Fundamentals of Astrodynamics and Applications (second ed.). Microcosm Press, El Segundo, CA. ISBN 1-881883-12-4. , p. 153
Look up ecliptic in Wiktionary, the free dictionary.

Retrieved from "https://en.wikipedia.org/w/index.php?title=Ecliptic&oldid=524829192"