Standard RAID levels

The standard RAID levels are a basic set of RAID configurations that employ the techniques of striping, mirroring, or parity to large reliable data stores from general purpose computer hard disk drives. The most common types today are RAID 0 (striping), RAID 1 and variants (mirroring), RAID 5 (distributed parity) and RAID 6 (dual parity).

Alternatives to the above designs include non-standard RAID levels and non-RAID drive architectures. RAID levels and their associated data formats are standardized by SNIA in the Common RAID Disk Drive Format (DDF) standard.

RAID 0

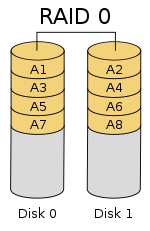
A RAID 0 (also known as a stripe set or striped volume) splits data evenly across two or more disks (striped) without parity information for speed. RAID 0 was not one of the original RAID levels and provides no data redundancy. RAID 0 is normally used to increase performance, although it can also be used as a way to create a large logical disk out of two or more physical ones.

A RAID 0 can be created with disks of differing sizes, but the storage space added to the array by each disk is limited to the size of the smallest disk. For example, if a 100 GB disk is striped together with a 350 GB disk, the size of the array will be 200 GB (100 GB x 2).

{\begin{aligned}\mathrm {Size} &=2\cdot \min \left(100\,\mathrm {GB} ,350\,\mathrm {GB} \right)\\&=2\cdot 100\,\mathrm {GB} \\&=200\,\mathrm {GB} \end{aligned}}

The diagram shows the how data is distributed into Ax stripes to the disks. Accessing the stripes in the order A1, A2, A3, ... provides the illusion of a larger and faster drive. Once the stripe size is defined on creation it needs to be maintained at all times.

Performance

While the block size can technically be as small as a byte, it is almost always a multiple of the hard disk sector size of 512 bytes. This lets each drive seek independently when randomly reading or writing data on the disk. How much the drives act independently depends on the access pattern from the file system level. For reads and writes that are larger than the stripe size, such as copying files or video playback, the disks will be seeking to the same position on each disk, so the seek time of the array will be the same as that of a single drive. For reads and writes that are smaller than the stripe size, such as database access, the drives will be able to seek independently. If the sectors accessed are spread evenly between the two drives, the apparent seek time of the array will be half that of a single drive (assuming the disks in the array have identical access time characteristics). The transfer speed of the array will be potentially the transfer speed of all the disks added together, limited only by the speed of the RAID controller. Approaching this limit, however, assumes optimal access patterns and perfect disk operation.

RAID 0 is useful for setups such as large read-only NFS servers where mounting many disks is time-consuming or impossible and redundancy is irrelevant.

RAID 0 is also used in some computer gaming systems where performance is desired and data integrity is not very important. However, real-world tests with computer games have shown that RAID-0 performance gains are minimal, although some desktop applications will benefit.^[1]^[2] Another article examined these claims and concludes: "Striping does not always increase performance (in certain situations it will actually be slower than a non-RAID setup), but in most situations it will yield a significant improvement in performance." ^[3]

RAID 1

An exact copy (or mirror) of a set of data on two disks. This is useful when read performance or reliability is more important than data storage capacity. Such an array can only be as big as the smallest member disk. A classic RAID 1 mirrored pair contains two disks (see reliability geometrically) over a single disk. Since each member contains a complete copy and can be addressed independently, ordinary wear-and-tear reliability is raised by the power of the number of self-contained copies.

Essentially, since both disks contain the exact same data, read access can be be conducted to any single disk alone – A1 is the same for disk 0 or disk 1. Alternatively, they can be done like on a RAID 0 pair with an arbitrary stripe size. Writes are simply duplicated for both drives.

Performance

Since all the data exists in two or more copies, each with its own hardware, the read performance can go up roughly as a linear multiple of the number of copies. That is, a RAID 1 array of two drives can be reading in two different places at the same time, though not all implementations of RAID 1 do this.^[4] To maximize performance benefits of RAID 1, independent disk controllers are recommended, one for each disk. Some refer to this practice as splitting or duplexing (for two disk arrays) or multiplexing (for arrays with more than two disks). When reading, both disks can be accessed independently and requested sectors can be split evenly between the disks. For the usual mirror of two disks, this would, in theory, double the transfer rate when reading. The apparent access time of the array would be half that of a single drive. Unlike RAID 0, this would be for all access patterns, as all the data are present on all the disks. In reality, the need to move the drive heads to the next block (to skip blocks already read by the other drives) can effectively mitigate speed advantages for sequential access. Read performance can be further improved by adding drives to the mirror. Many older IDE RAID 1 controllers read only from one disk in the pair, so their read performance is always that of a single disk. Some older RAID 1 implementations read both disks simultaneously to compare the data and detect errors. The error detection and correction on modern disks makes this less useful in environments requiring normal availability. When writing, the array performs like a single disk, as all mirrors must be written with the data. Note that these are best case performance scenarios with optimal access patterns.

RAID 1 has many administrative advantages. For instance, in some environments, it is possible to "split the mirror," declare one disk as inactive, do a backup of that disk, then "rebuild" the mirror. This is useful in situations where the file system must be constantly available. This requires that the application supports recovery from the image of data on the disk at the point of the mirror split. This procedure is less critical in the presence of the "snapshot" feature of some file systems, in which some space is reserved for changes, presenting a static point-in-time view of the file system. Alternatively, a new disk can be substituted so that the inactive disk can be kept in much the same way as traditional backup. To maintain redundancy during the backup process, some controllers support adding a third disk to an active pair. After the third disk rebuild completes, it is made inactive and backed up as described above.

RAID 2

A RAID 2 stripes data at the bit (rather than block) level, and uses Hamming code for error correction. The disks are synchronized by the controller to spin at the same angular orientation (they reach Index at the same time). Extremely high data transfer rates are possible. This is the only original level of RAID that is not currently used.^[5]^[6]

The use of Hamming(7,4) code (four data bits plus three parity bits) also permits using seven disks in RAID 2, with four being used for data storage and three being used for error correction.

RAID 2 is the only standard RAID level, other than some implementations of RAID 6, which can automatically recover accurate data from single-bit corruption in data. Other RAID levels can detect single-bit corruption in data, or can sometimes reconstruct missing data, but cannot reliably resolve contradictions between parity bits and data bits without human intervention.

(Multiple-bit corruption is possible, though extremely rare. RAID 2 can detect, but not repair, double-bit corruption.)

All hard disks eventually implemented Hamming code error correction. This made RAID 2 error correction redundant and unnecessarily complex. Like RAID 3, this level quickly became useless and is now obsolete. There are no commercial applications of RAID 2.^[5]^[6]

RAID 3

A RAID 3 uses byte-level striping with a dedicated parity disk. RAID 3 is very rare in practice. One of the characteristics of RAID 3 is that it generally cannot service multiple requests simultaneously. This happens because any single block of data will, by definition, be spread across all members of the set and will reside in the same location. So, any I/O operation requires activity on every disk and usually requires synchronized spindles.

In our example, a request for block "A" consisting of bytes A1–A6 would require all three data disks to seek to the beginning (A1) and reply with their contents. A simultaneous request for block B would have to wait.

However, the performance characteristic of RAID 3 is very consistent, unlike that for higher RAID levels.^{[clarification needed]} The size of a stripe is less than the size of a sector or OS block. As a result, reading and writing accesses the entire stripe every time. The performance of the array is therefore identical to the performance of one disk in the array except for the transfer rate, which is multiplied by the number of data drives less the parity drives.

This makes it best for applications that demand the highest transfer rates in long sequential reads and writes, for example uncompressed video editing. Applications that make small reads and writes from random disk locations will get the worst performance out of this level.^[6]

The requirement that all disks spin synchronously, a.k.a. lockstep, added design considerations to a level that didn't give significant advantages over other RAID levels, so it quickly became useless and is now obsolete.^[5] Both RAID 3 and RAID 4 were quickly replaced by RAID 5.^[7] RAID 3 was usually implemented in hardware, and the performance issues were addressed by using large disk caches.^[6]

RAID 4

A RAID 4 uses block-level striping with a dedicated parity disk. This allows each member of the set to act independently when only a single block is requested. If the disk controller allows it, a RAID 4 set can service multiple read requests simultaneously. RAID 4 looks similar to RAID 5 except that it does not use distributed parity, and similar to RAID 3 except that it stripes at the block level, rather than the byte level. Generally, RAID 4 is implemented with hardware support for parity calculations, and a minimum of three disks is required for a complete RAID 4 configuration.

In the example on the right, a read request for block A1 would be serviced by disk 0. A simultaneous read request for block B1 would have to wait, but a read request for B2 could be serviced concurrently by disk 1.

For writing, the parity disk becomes a bottleneck, as simultaneous writes to A1 and B2 would, in addition to the writes to their respective drives, also both need to write to the parity drive. In this way RAID 4 places a very high load on the parity drive in an array.

The performance of RAID 4 in this configuration can be very poor, but unlike RAID 3 it does not need synchronized spindles. However, if RAID 4 is implemented on synchronized drives and the size of a stripe is reduced below the OS block size a RAID 4 array then has the same performance pattern as a RAID 3 array.

RAID 4 is very uncommon, but one enterprise level company to use it is NetApp. The aforementioned performance problems were solved with their proprietary Write Anywhere File Layout (WAFL), an approach to writing data to disk locations that minimizes the conventional parity RAID write penalty. By storing system metadata (inodes, block maps, and inode maps) in the same way application data is stored, WAFL is able to write file system metadata blocks anywhere on the disk. This approach in turn allows multiple writes to be "gathered" and scheduled to the same RAID stripe—eliminating the traditional read-modify-write penalty prevalent in parity-based RAID schemes.^[8] A conspicuous advantage of both RAID 3 and RAID 4 is that zeroed disks may be added to RAID groups without affecting parity. This advantage—important during the '90s—has diminished somewhat with time and the increasing prevalence of virtualized systems.

Both RAID 3 and RAID 4 have been replaced by RAID 5 and RAID 6 in most commercial systems.

RAID 5

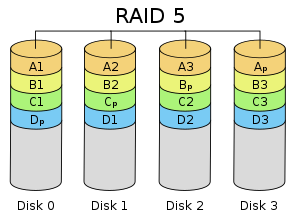
A RAID 5 uses block-level striping with parity data distributed across all member disks. RAID 5 has achieved popularity because of its low cost of redundancy. This can be seen by comparing the number of drives needed to achieve a given capacity. For an array of $n$ drives, with $S_{\mathrm {min} }$ being the size of the smallest disk in the array, other RAID levels that yield redundancy give only a storage capacity of $S_{\mathrm {min} }$ (for RAID 1), or $S_{\mathrm {min} }\times (n/2)$ (for RAID 1+0). In RAID 5, the yield is $S_{\mathrm {min} }\times (n-1)$ . For example, four 1 TB drives can be made into two separate 1 TB redundant arrays under RAID 1 or 2 TB under RAID 1+0, but the same four drives can be used to build a 3 TB array under RAID 5. Although RAID 5 may be implemented in a disk controller, some have hardware support for parity calculations (hardware RAID cards with onboard processors) while some use the main system processor (a form of software RAID in vendor drivers for inexpensive controllers). Many operating systems also provide software RAID support independently of the disk controller, such as Windows Dynamic Disks, Linux mdadm, or RAID-Z. In most implementations, a minimum of three disks is required for a complete RAID 5 configuration. In some implementations a degraded RAID 5 disk set can be made (three disk set of which only two are online), while mdadm supports a fully functional (non-degraded) RAID 5 setup with two disks - which functions as a slow RAID-1, but can be expanded with further volumes.

In the example, a read request for block A1 would be serviced by disk 0. A simultaneous read request for block B1 would have to wait, but a read request for B2 could be serviced concurrently by disk 1.

Parity handling

A concurrent series of blocks - one on each of the disks in an array - is collectively called a stripe. If another block, or some portion thereof, is written on that same stripe, the parity block, or some portion thereof, is recalculated and rewritten. For small writes, this requires:

Read the old data block
Read the old parity block
Compare the old data block with the write request. For each bit that has flipped (changed from 0 to 1, or from 1 to 0) in the data block, flip the corresponding bit in the parity block
Write the new data block
Write the new parity block

The disk used for the parity block is staggered from one stripe to the next, hence the term distributed parity blocks. RAID 5 writes are expensive in terms of disk operations and traffic between the disks and the controller.

The parity blocks are not read on data reads, since this would add unnecessary overhead and would diminish performance. The parity blocks are read, however, when a read of blocks in the stripe fails due to failure of any one of the disks, and the parity block in the stripe are used to reconstruct the errant sector. The CRC error is thus hidden from the main computer. Likewise, should a disk fail in the array, the parity blocks from the surviving disks are combined mathematically with the data blocks from the surviving disks to reconstruct the data from the failed drive on-the-fly.

This is sometimes called Interim Data Recovery Mode. The computer knows that a disk drive has failed, but this is only so that the operating system can notify the administrator that a drive needs replacement; applications running on the computer are unaware of the failure. Reading and writing to the drive array continues seamlessly, though with some performance degradation.

Latency

When a disk record is randomly accessed there is a delay as the disk rotates sufficiently for the data to come under the head for processing. This delay is called latency. On average, a single disk will need to rotate 1/2 revolution. Thus, for a 7200 RPM disk the average latency is 4.2 milliseconds. In RAID 5 arrays all the disks must be accessed so the latency can become a significant factor. In a RAID 5 array, with n randomly oriented disks, the mean latency is ${\frac {n}{n+1}}$ revolutions and the median latency is $2^{-1/n}$ . In order to mitigate this problem, well-designed RAID systems will synchronize the angular orientation of their disks. In this case the random nature of the angular displacements goes away, the average latency returns to 1/2 revolution, and a saving of up to 50% in latency is achieved. Since solid state drives do not have disks, their latency does not follow this model.

Effect of Angular Desynchronization
Number of Disks	Mean Latency (Rev)	Median Latency (Rev)
1	0.50	0.50
2	0.67 (+33%)</small>	0.71 (+41%)</small>
3	0.75 (+50%)</small>	0.79 (+59%)</small>
4	0.80 (+60%)</small>	0.84 (+68%)</small>
5	0.83 (+67%)</small>	0.87 (+74%)</small>
6	0.86 (+71%)</small>	0.89 (+78%)</small>
7	0.88 (+75%)</small>	0.91 (+81%)</small>
8	0.89 (+78%)</small>	0.92 (+83%)</small>

Usable capacity

Parity uses up the capacity of one drive in the array. (This can be seen by comparing it with RAID 4: RAID 5 distributes the parity data across the disks, while RAID 4 centralizes it on one disk, but the amount of parity data is the same.) If the drives vary in capacity, the smallest one sets the limit. Therefore, the usable capacity of a RAID 5 array is $(N-1)\cdot S_{\mathrm {min} }$ , where $N$ is the total number of drives in the array and $S_{\mathrm {min} }$ is the capacity of the smallest drive in the array.

The number of hard disks that can belong to a single array is limited only by the capacity of the storage controller in hardware implementations, or by the OS in software RAID. One caveat is that unlike RAID 1, as the number of disks in an array increases, the probability of data loss due to multiple drive failures also increases. This is because there is a reduced ratio of "losable" drives (the number of drives that can fail before data is lost) to total drives.

RAID 6

RAID 6 extends RAID 5 by adding an additional parity block; thus it uses block-level striping with two parity blocks distributed across all member disks.

Performance (speed)

RAID 6 does not have a performance penalty for read operations, but it does have a performance penalty on write operations because of the overhead associated with parity calculations. Performance varies greatly depending on how RAID 6 is implemented in the manufacturer's storage architecture – in software, firmware or by using firmware and specialized ASICs for intensive parity calculations. It can be as fast as a RAID-5 system with one fewer drive (same number of data drives).^[9]

Efficiency (potential waste of storage)

RAID 6 is no more space inefficient than RAID 5 with a hot spare drive when used with a small number of drives, but as arrays become bigger and have more drives, the loss in storage capacity becomes less important, although the probability of data loss is greater with larger arrays. RAID 6 provides protection against data loss during an array rebuild, when a second drive is lost, a bad block read is encountered, or when a human operator accidentally removes and replaces the wrong disk drive when attempting to replace a failed drive.

The usable capacity of a RAID 6 array is $(N-2)\cdot S_{\mathrm {min} }$ , where $N$ is the total number of drives in the array and $S_{\mathrm {min} }$ is the capacity of the smallest drive in the array.

Implementation

According to the Storage Networking Industry Association (SNIA), the definition of RAID 6 is: "Any form of RAID that can continue to execute read and write requests to all of a RAID array's virtual disks in the presence of any two concurrent disk failures. Several methods, including dual check data computations (parity and Reed-Solomon), orthogonal dual parity check data and diagonal parity, have been used to implement RAID Level 6."^[10]

Computing parity

Two different syndromes need to be computed in order to allow the loss of any two drives. One of them, P can be the simple XOR of the data across the stripes, as with RAID 5. A second, independent syndrome is more complicated and requires the assistance of field theory.

To deal with this, the Galois field $GF(m)$ is introduced with $m=2^{k}$ , where $GF(m)\cong F_{2}[x]/(p(x))$ for a suitable irreducible polynomial $p(x)$ of degree $k$ . A chunk of data can be written as $d_{k-1}d_{k-2}...d_{0}$ in base 2 where each $d_{i}$ is either 0 or 1. This is chosen to correspond with the element $d_{k-1}x^{k-1}+d_{k-2}x^{k-2}+...+d_{1}x+d_{0}$ in the Galois field. Let $D_{0},...,D_{n-1}\in GF(m)$ correspond to the stripes of data across hard drives encoded as field elements in this manner (in practice they would probably be broken into byte-sized chunks). If $g$ is some generator of the field and $\oplus$ denotes addition in the field while concatenation denotes multiplication, then $\mathbf {P}$ and $\mathbf {Q}$ may be computed as follows ( $n$ denotes the number of data disks):

\mathbf {P} =\bigoplus _{i}{D_{i}}=\mathbf {D} _{0}\;\oplus \;\mathbf {D} _{1}\;\oplus \;\mathbf {D} _{2}\;\oplus \;...\;\oplus \;\mathbf {D} _{n-1}

\mathbf {Q} =\bigoplus _{i}{g^{i}D_{i}}=g^{0}\mathbf {D} _{0}\;\oplus \;g^{1}\mathbf {D} _{1}\;\oplus \;g^{2}\mathbf {D} _{2}\;\oplus \;...\;\oplus \;g^{n-1}\mathbf {D} _{n-1}

For a computer scientist, a good way to think about this is that $\oplus$ is a bitwise XOR operator and $g^{i}$ is the action of a linear feedback shift register on a chunk of data. Thus, in the formula above,^[11] the calculation of P is just the XOR of each stripe. This is because addition in any characteristic two finite field reduces to the XOR operation. The computation of Q is the XOR of a shifted version of each stripe.

Mathematically, the generator is an element of the field such that $g^{i}$ is different for each nonnegative $i$ satisfying $i<n$ .

If one data drive is lost, the data can be recomputed from P just like with RAID 5. If two data drives are lost or a data drive and the drive containing P are lost, the data can be recovered from P and Q or from just Q, respectively, using a more complex process. Working out the details is extremely hard with field theory. Suppose that $D_{i}$ and $D_{j}$ are the lost values with $i\neq j$ . Using the other values of $D$ , constants $A$ and $B$ may be found so that $D_{i}\oplus D_{j}=A$ and $g^{i}D_{i}\oplus g^{j}D_{j}=B$ :

A=\bigoplus _{\ell :\;\ell \not =i\;\mathrm {and} \;\ell \not =j}{D_{\ell }}=\mathbf {P} \;\oplus \;\mathbf {D} _{0}\;\oplus \;\mathbf {D} _{1}\;\oplus \;\dots \;\oplus \;\mathbf {D} _{i-1}\;\oplus \;\mathbf {D} _{i+1}\;\oplus \;\dots \;\oplus \;\mathbf {D} _{j-1}\;\oplus \;\mathbf {D} _{j+1}\;\oplus \;\dots \;\oplus \;\mathbf {D} _{n-1}

B=\bigoplus _{\ell :\;\ell \not =i\;\mathrm {and} \;\ell \not =j}{g^{\ell }D_{\ell }}=\mathbf {Q} \;\oplus \;g^{0}\mathbf {D} _{0}\;\oplus \;g^{1}\mathbf {D} _{1}\;\oplus \;\dots \;\oplus \;g^{i-1}\mathbf {D} _{i-1}\;\oplus \;g^{i+1}\mathbf {D} _{i+1}\;\oplus \;\dots \;\oplus \;g^{j-1}\mathbf {D} _{j-1}\;\oplus \;g^{j+1}\mathbf {D} _{j+1}\;\oplus \;\dots \;\oplus \;g^{n-1}\mathbf {D} _{n-1}

Multiplying both sides of the equation for $B$ by $g^{n-i}$ and adding to the former equation yields $(g^{n-i+j}\oplus 1)D_{j}=g^{n-i}B\oplus A$ and thus a solution for $D_{j}$ , which may be used to compute $D_{i}$ .

The computation of Q is CPU intensive compared to the simplicity of P. Thus, a RAID 6 implemented in software will have a more significant effect on system performance, and a hardware solution will be more complex.

Composite RAID architectures

An important thing to realize about RAID is that the concepts can be generalized to generic storage elements and not limited to classical physical disks. Further, this means that a RAID array may be made of RAID arrays, a critical concept for enterprise-scale storage solutions. However, as both software and hardware RAID solutions on commodity hardware (including PCs) advance, these architectures become realistic for less-exotic applications. A large number of combinations are possible; the following are merely some of the most common, and illustrate some of the design decisions required.

"RAID 10": a stripe made of mirrors

So-called RAID 10 arrays consist of a top-level RAID-0 array (or stripe set) composed of two or more RAID-1 arrays (or mirrors). A single-drive failure in a RAID 10 configuration results in one of the lower-level mirrors entering degraded mode, but the top-level stripe may be configured to perform normally (except for the performance hit), as both of its constituent storage elements are still operable—this is application-specific.

The failed drive is replaced with a spare, the low-level mirror is rebuilt from the remaining good drive(s), and no change is necessary for the stripe set. (Though the performance of the top-level RAID 0 stripe set will be degraded during the rebuild of the low-level RAID-1 mirror, stripe sets do not have a degraded mode per se).

"RAID 0+1": a mirror made of stripes

In contrast to RAID 10, so-called RAID 0+1 arrays consist of a top-level RAID-1 mirror composed of two or more RAID-0 stripe sets. A single-drive failure in a RAID 0+1 configuration results in one of the lower-level stripes completely failing (as RAID 0 is not fault tolerant), while the top-level mirror enters degraded mode.

The failed drive must be replaced with a spare, the stripe set must be rebuilt as an empty array, and then the mirror is rebuilt onto the empty stripe set by copying from the stripe set which did not experience a failure.

Whether RAID 0+1 is preferable to RAID 10 depends on the details of the application in question, such as what level of performance is required during degraded operation, or during a rebuild. Also, as for any RAID array, whether or not the array can be rebuilt on-line (without interrupting user services) depends on the hardware, operating system, and configuration in use.

Non-standard RAID levels and non-RAID drive architectures

There are other RAID levels that are promoted by individual vendors, but not generally standardized. The non-standard RAID levels 5E, 5EE and 6E extend RAID 5 and 6 with hot-spare drives.

Other non-standard RAID levels include:

RAID 1.5
RAID 7 (a hardware-supported, proprietary RAID developed by Storage Computer Corp. of Nashua, NH)
RAID-DP
RAID S or parity RAID
Matrix RAID
RAID-K
ZFS RAID-Z
RAIDn
Linux MD RAID 10
IBM ServeRAID 1E
unRAID
ineo Complex RAID
Drobo BeyondRAID
Synology Hybrid RAID
Microsoft Storage Spaces

There are also non-RAID drive architectures, which are referred to by similar acronyms, notably SLED, Just a Bunch of Disks, SPAN/BIG, and MAID.

References

^ "Western Digital's Raptors in RAID-0: Are two drives better than one?". AnandTech. July 1, 2004. Retrieved 2007-11-24.
^ "Hitachi Deskstar 7K1000: Two Terabyte RAID Redux". AnandTech. April 23, 2007. Retrieved 2007-11-24.
^ "RAID 0: Hype or blessing?". Tweakers.net. August 7, 2004. Retrieved 2008-07-23.
^ "Mac OS X, Mac OS X Server: How to Use Apple-Supplied RAID Software". Apple.com. Retrieved 2007-11-24.
^ ^a ^b ^c Derek Vadala (2003). Managing RAID on Linux. O'Reilly Series (illustrated ed.). O'Reilly. p. 6. ISBN 1-56592-730-3, 9781565927308. {{cite book}}: Check |isbn= value: invalid character (help)
^ ^a ^b ^c ^d Evan Marcus, Hal Stern (2003). Blueprints for high availability (2, illustrated ed.). John Wiley and Sons. p. 167. ISBN 0-471-43026-9, 9780471430261. {{cite book}}: Check |isbn= value: invalid character (help)
^ Michael Meyers, Scott Jernigan (2003). Mike Meyers' A+ Guide to Managing and Troubleshooting PCs (illustrated ed.). McGraw-Hill Professional. p. 321. ISBN 0-07-223146-7, 9780072231465. {{cite book}}: Check |isbn= value: invalid character (help)
^ http://partners.netapp.com/go/techontap/matl/NetApp_DNA.html
^ Rickard E. Faith (13 May 2009). "A Comparison of Software RAID Types". {{cite journal}}: Cite journal requires |journal= (help)
^ "Dictionary R". Storage Networking Industry Association. Retrieved 2007-11-24.
^ Anvin, H. Peter (21 May 2009). "The mathematics of RAID-6" (PDF). Retrieved November 4, 2009.

External links

[1] "Western Digital's Raptors in RAID-0: Are two drives better than one?". AnandTech. July 1, 2004. Retrieved 2007-11-24.

[2] "Hitachi Deskstar 7K1000: Two Terabyte RAID Redux". AnandTech. April 23, 2007. Retrieved 2007-11-24.

[3] "RAID 0: Hype or blessing?". Tweakers.net. August 7, 2004. Retrieved 2008-07-23.

[4] "Mac OS X, Mac OS X Server: How to Use Apple-Supplied RAID Software". Apple.com. Retrieved 2007-11-24.

[vadala-5] Derek Vadala (2003). Managing RAID on Linux. O'Reilly Series (illustrated ed.). O'Reilly. p. 6. ISBN 1-56592-730-3, 9781565927308. {{cite book}}: Check |isbn= value: invalid character (help)

[marcus-6] Evan Marcus, Hal Stern (2003). Blueprints for high availability (2, illustrated ed.). John Wiley and Sons. p. 167. ISBN 0-471-43026-9, 9780471430261. {{cite book}}: Check |isbn= value: invalid character (help)

[meyers-7] Michael Meyers, Scott Jernigan (2003). Mike Meyers' A+ Guide to Managing and Troubleshooting PCs (illustrated ed.). McGraw-Hill Professional. p. 321. ISBN 0-07-223146-7, 9780072231465. {{cite book}}: Check |isbn= value: invalid character (help)

[8] ttp://partners.netapp.com/go/techontap/matl/NetApp_DNA.html

[Faith-9] Rickard E. Faith (13 May 2009). "A Comparison of Software RAID Types". {{cite journal}}: Cite journal requires |journal= (help)

[SNIA-def-10] "Dictionary R". Storage Networking Industry Association. Retrieved 2007-11-24.

[11] Anvin, H. Peter (21 May 2009). "The mathematics of RAID-6" (PDF). Retrieved November 4, 2009.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

RAID 0

Performance

RAID 1

Performance

RAID 2

RAID 3

RAID 4

RAID 5

Parity handling

Latency

Usable capacity

RAID 6

Performance (speed)

Efficiency (potential waste of storage)

Implementation

Computing parity

Composite RAID architectures

"RAID 10": a stripe made of mirrors

"RAID 0+1": a mirror made of stripes

Non-standard RAID levels and non-RAID drive architectures

See also

References

External links