Regular diatonic tuning

12-tone , 72-tone (Maneri-Sims notation) , and also (both written the same as 12-tone in Easley Blackwood notation) 17-tone and 19-tone regular diatonic scales

T and S in various equal temperaments (*5-tone and 7-tone are the limits of and not regular diatonic tunings) and

A regular diatonic tuning is any musical scale consisting of "tones" (T) and "semitones" (S) arranged in any rotation of the sequence TTSTTTS which adds up to the octave with all the T's being the same size and all the S's the being the same size, with the 'S's being smaller than the 'T's.

Overview

In the ordinary diatonic scales the T's here are tones and the S's are semitones which are half, or approximately half the size of the tone. But in the more general regular diatonic tunings, the two steps can be of any relation within the range between T=171.43 (S=T) and T=240 (S=0) cents (fifth between 685.71 and 720). Note that regular diatonic tunings are not limited to the notes of the diatonic scale which defines them.

One may determine the corresponding cents of S, T, and the fifth, given one of the values:

• S = (1200-(T*5))/2
• T = (1200-(S*2))/5
• The fifth = (T+1200)/2

When the S's reduce to zero (T=240 cents) the result is TTTTT or a five tone equal temperament. As the semitones get larger, eventually the steps are all the same size, and the result is in seven tone equal temperament (S=T=171.43). These two end points are not included as regular diatonic tunings, because to be regular the pattern of large and small steps has to be preserved, but everything in between is included, however small the semitones are, or however similar they are to the whole tones.

"Regular" here is understood in the sense of a mapping from Pythagorean diatonic such that all the interval relationships are preserved. For instance, in all regular diatonic tunings, just as for the pythagorean diatonic:

• The notes are connected together through a chain of six fifths reduced to the octave, or equivalently, through ascending fifths and descending fourths (e.g. F, C, G, D, A, E, B, in C major).
• A chain of two equal sized fifths (reduced to the octave) generates a tone (e.g. C G D)
• A chain of five fourths generates a semitone in the same way (e.g. E, A, D, G, C, F)
• A chain of four equal sized fifths (E.g. C, G, D, A, E) generates a major third consisting of two whole tones
• A chain of three fourths generates a minor third (A, D, G, C)

and so on; in all those examples the result is reduced to the octave.

If one continues to increase the size of the S further, so that it is larger than the T, one gets scales with two large steps and five small steps, and eventually, when all the T's vanish the result is SS, so a tritone division of the octave. These scales however are not included as regular diatonic tunings.

All regular diatonic tunings are also Linear temperaments, i.e. Regular temperaments with two generators: the octave and the tempered fifth. One can use the tempered fourth as an alternative generator (e.g. as B E A D G C F, ascending fourths, reduced to the octave), but the tempered fifth is the more usual choice.

All regular diatonic tunings are also Generated collections (also called Moments of Symmetry) and the chain of fifths can be continued in either direction to obtain a twelve tone system F C G D A E B F# C# G# D# A# where the interval F#-G is the same as B - C etc., another moment of symmetry with two interval sizes. A chain of seven fifths generates a chromatic semitone, for instance from F to F# and the pattern of chromatic and diatonic semitones is CDCDDCDCDCDD or a permutation of it where the C is the chromatic semitone, and D is the diatonic semitone e.g. from E to F between notes five steps apart in the cycle. Here, the seven equal system is the limit as the chromatic semitone tends to zero, and the five tone system in the limit as the diatonic semitone tends to zero.

Range of recognizability

The regular diatonic tunings include all linear temperaments within Easely Blackwood's "Range of Recognizabilty" in his The Structure of Recognizable Diatonic Tunings for diatonic tunings with

• the fifth tempered to between 4/7 and 3/5 of an octave,
• major and minor seconds both positive
• major second larger than the minor second,.

However, his "range of recognizability" is more restrictive than "regular diatonic tuning". For instance, he requires the diatonic semitone to be at least 25 cents in size. See for a summary.

Significant regions within the range

When the fifths are a little flatter than the 700 cents of the diatonic subset of twelve equal, then we are in the region of the historical meantone tunings, which distribute or temper out the syntonic comma. This includes

• 1/3 comma meantone - achieves pure minor thirds 6/5, fifth is 694.786 cents. It's closely approximated by the diatonic scale in 19 equal temperament
• 1/4 comma meantone - achieves pure major thirds 5/4 (386.313), fifth is 696.6 cents, closely approximated in 31 tone equal temperament
• 1/6 comma meantone - achieves a pure diatonic tritone 45/32, fifth is 698.371 cents, closely approximated in 55 tone equal temperament
• 1/11 comma meantone - fifth is 699.99988 cents, almost indistinguishable from twelve equal temperament

When the fifths are exactly 3/2, or around 702 cents, the result is the Pythagorean diatonic tuning.

For fifths slightly narrower than 3/2, the result is a Schismatic temperament, where the temperament is measured in terms of a fraction of a schisma - the amount by which a chain of eight fifths reduced to an octave is sharper than the just minor sixth 8/5. So for instance, a 1/8 schizma temperament will achieve a pure 8/5 in an ascending chain of eight fifths. 53 equal temperament achieves a good approximation to Schismatic temperament.

At around 703.4-705.0 cents, with fifths mildly tempered in the wide direction, the result is major thirds with ratios near 14/11 (417.508 cents) and minor thirds around 13/11 (289.210 cents).

At 705.882 cents, or tempered in the wide direction by 3.929 cents, the result is the diatonic scale in 17 tone equal. Beyond this point, the regular major and minor thirds approximate simple ratios of numbers with prime factors 2-3-7, such as the 9/7 or septimal major third (435.084 cents) and 7/6 or septimal minor third (266.871 cents). At the same time, the regular tones more and more closely approximate a large 8/7 tone (231.174 cents), and regular minor sevenths the "harmonic seventh" at the simple ratio of 7/4 (968.826 cents). This septimal range extends out to around 711.111 cents or 27-ed2, or a bit further.

That leaves the two extremes, what we could call:

• the "inframeantone" range with fifths between the lower bound for the regular diatonic of 7-ed2 (685.7143 cents) and the range of historical meantones beginning around 1/3-comma or 19-ed2 (694.786 cents), and with the diatonic "semitones" approaching the size of the diatonic whole tone
• the "ultraseptimal" range from around 712 cents all the way to the upper bound of the regular diatonic at 720 cents or 5-ed2, and with very small diatonic semitones

Diatonic scales constructed in equal temperaments can have fifths either wider or narrower than a just 3/2. Here are a few examples:

• 12 (and its multiples), 15, 17, 22, have fifths wider than a just 3/2
• 19, 31, 53, have fifths narrower than a just 3/2

Syntonic temperament and timbre

Regular diatonic tunings have also been referred to as syntonic temperaments. This terminology is used for an instrument able to adjust timbre and use inharmonic partials in order to approximate the smoothness of 5/4 in harmonic timbres using inharmonic instruments with tempered fifths anywhere in the range of the regular diatonic tunings. It is named after the syntonic comma because of the resemblance to quarter comma meantone where the syntonic comma is tempered out. In the syntonic temperament on this instrument, then the syntonic comma is not tempered out, but the partials are adjusted to give a similar sound to the pure major thirds of quarter comma meantone while also preserving its characteristic that the major third is made up of two equally sized tones.

Figure 1: The syntonic temperament's tuning continuum, from (Milne et al. 2007).

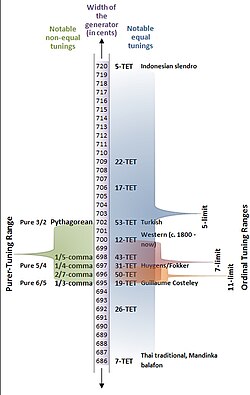
Since it's a linear temperament, it can be played on an isomorphic keyboard, on which the fingering-pattern of any given musical structure is the same in any syntonic tuning. The combination of an isomorphic keyboard and continuously variable tuning enables Dynamic tonality, a novel expansion of the framework of tonality.

As shown in the figure at right, the tonally valid tuning range of the syntonic temperament includes a number of historically important tunings, such as the currently popular 12-tone equal division of the octave (12-edo tuning, also known as 12-tone “equal temperament”), the meantone tunings, and Pythagorean tuning. Tunings in the syntonic temperament can be equal (12-edo, 31-edo), non-equal (Pythagorean, meantone), circulating, and can move towards (approximate) some Just Intonation tunings.

Figure 2: Change in widths of intervals of the syntonic temperament across its tuning continuum (tonic is D).

The legend of Figure 2 (on the right side of the figure) shows a stack of P5's centered on D. Each resulting note represents an interval in the syntonic temperament with D as the tonic. The body of the figure shows how the widths (from D) of these intervals change as the width of the P5 is changed across the syntonic temperament's tuning continuum.

• At P5 ≈ 685.7 cents , the intervals converge on just 7 widths (assuming octave equivalence of 0 and 1200 cents), producing 7-edo. S/T = 0.
• At P5 ≈ 694.7 (19-edo), the gaps between these 19 intervals are all equal, producing 19-edo tuning. S/T = 2/3.
• At P5 ≈ 696.8 (31-edo), a stack of 31 such intervals would show equal gaps between each such interval, producing 31-edo tuning. S/T = 3/5.
• At P5 = 700.0 (12-edo), the sharp notes and flat notes are equal, producing 12-edo tuning. S/T = 1/2.
• At P5 ≈ 701.9 (53-edo), a stack of 53 such intervals - each just 3/44 of a cent short of a pure fifth - makes 31 octaves, producing 53-edo tuning. S/T = 4/9.
• etc....
• at P5 = 720.0 cents , the pitches converge on just 5 widths, producing 5-edo. S/T = 1.

Research projects regarding the syntonic temperament

• The research program Musica Facta investigates the musical theory of the syntonic temperament.