Hexany
This article needs additional citations for verification. (August 2018) |
In musical tuning systems, the hexany, invented by Erv Wilson,[1] represents one of the simplest structures found in his combination product sets.
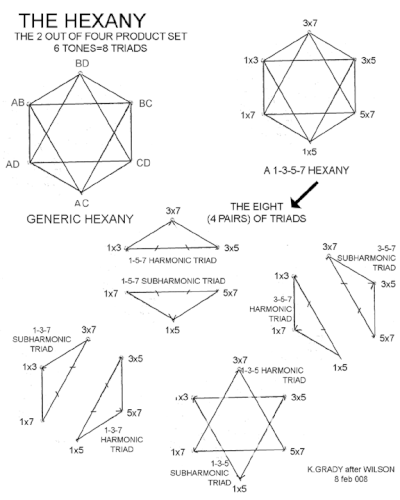
It is referred to as an uncentered structure, meaning that it implies no tonic. It achieves this by using consonant relations as opposed to the dissonance methods normally employed by atonality. While it is often and confusingly overlapped with the Euler–Fokker genus, the subsequent stellation of Wilson's combination product sets (CPS) are outside of that Genus. The Euler Fokker Genus fails to see 1 as a possible member of a set except as a starting point. The numbers of vertices of his combination sets follow the numbers in Pascal's triangle. In this construction, the hexany is the third cross-section of the four-factor set and the first uncentered one. hexany is the name that Erv Wilson gave to the six notes in the 2-out-of-4 combination product set, abbreviated as 2*4 CPS.[2]
Simply, the hexany is the 2 out of 4 set. It is constructed by taking any four factors and a set of two at a time, then multiplying them in pairs. For instance, the harmonic factors 1, 3, 5 and 7 are combined in pairs of 1*3, 1*5, 1*7, 3*5, 3*7, 5*7, resulting in 1, 3, 5, 7 Hexanies. The notes are usually octave shifted to place them all within the same octave, which has no effect on interval relations and the consonance of the triads. The possibility of an octave being a solution is not outside of Wilson's conception and is used in cases of placing larger combination product sets upon Generalized Keyboards.
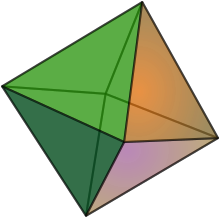
The hexany can be thought of as analogous to the octahedron. The notes are arranged so that each point represents a pitch, each edge an interval and each face a triad. It thus has eight just intonation triads where each triad has two notes in common with three of the other chords. Each triad occurs just once with its inversion represented by the opposing 3 tones. The edges of the octahedron show musical intervals between the vertices, usually chosen to be consonant intervals from the harmonic series. The points represent musical notes, and the three notes that make each of the triangular faces represent musical triads. Wilson also pointed out and explored the idea of melodic Hexanies.
Tuning
[edit]This shows the three dimensional version of the hexany.
The hexany is the figure containing both the triangles shown as well as the connecting lines between them.
In this 2D construction the interval relationships are the same. See also figure two of Kraig Grady's paper.[3]
For example, the face with vertices 3×5, 1×5, 5×7 is an otonal (major type) chord since it can be written as 5×(1, 3, 7), using low numbered harmonics. The 5×7, 3×7, 3×5 is a utonal (minor type) chord since it can be written as 3×5×7×(1/3, 1/5, 1/7), using low-numbered subharmonics.
To make this into a conventional harmonic construct with 1/1 as the first note, all the notes are first reduced to the octave. Since the harmonic construct as Erv called it as he did not consider it a scale and it does not have a 1/1 yet, any note chosen can be used to divide every note up to octave reduction. The ratios' notation here shows the ratios of the frequencies of the notes. If the 1/1 is 500 hertz, then 6/5 is 600 hertz, and so forth.
In music
[edit]Composers including Kraig Grady, Daniel James Wolf, and Joseph Pehrson have used pitch structures based on hexanies.[citation needed]
See also
[edit]References
[edit]- ^ Chalmers, John H. (1993). Divisions of the Tetrachord: a Prolegomenon to the Construction of Musical Scales, p.116. Frog Peak Music. ISBN 978-0-945996-04-0.
- ^ [author missing] (1993). Musicworks, Issues 55–60, p.43. Music Gallery.
- ^ Grady, Kraig (1991). "Ervin Wilson's Hexany" (PDF). Just Intonation. 7 (1): 8–11.
Further reading
[edit]- Narushima, Terumi (2018). Microtonality and the tuning systems of Erv Wilson. London. ISBN 978-1-315-71858-3. OCLC 1019658301.
{{cite book}}: CS1 maint: location missing publisher (link) - Grady, Kraig (1991), "Ervin Wilson's Hexany" (PDF), Just Intonation, vol. 7, no. 1, pp. 8–11
- Schiemer, Greg, "Tempered Dekanies: Chorus effect using microtonal intervals based on just intonation" (PDF), Proceedings of the 7th International Conference on Music Perception and Cognition, Sydney, 2002, pp. 300–302 [dead link] (see the Background section)
- Wilson, Erv. "D'Alessandro, Like a Hurricane" (PDF). Xenharmonikon. 12: 10, 21.
External links
[edit]- "Some hexany and hexany Diamond Lattices (and Blanks)", The Wilson Archives. Original hexany papers showing different facets and configurations, not assembled by Erv Wilson (1967 on)
- "The Wilson Archives", Anaphoria.com
- "hexany", RobertInventor.com. With a hexany you can turn around and click on any of its vertices, edges, or faces to hear the chords.
- "Combination-Product Set Patterns", Xenharmonikon IX (1986) by Kraig Grady.
- "Eikosany Papers", Anaphoria.com.
- "Musical Geometry", Music and Virtual Flowers. Intro. to musical geometry.
- "The Tumbling Dekany", "Unusual musical scales", Dave Keenan's Home Page. Dave Keenan's Dekany tumbling in 4 dimensions — as a musical Excel spreadsheet