3-3 duoprism

3-3 duoprism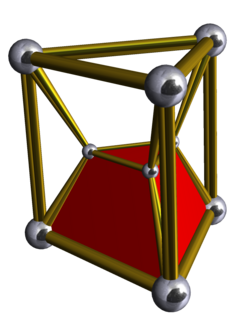 Schlegel diagram
Type	Uniform duoprism
Schläfli symbol	{3}×{3} = {3}²
Coxeter diagram
Cells	6 triangular prisms
Faces	9 squares, 6 triangles
Edges	18
Vertices	9
Vertex figure	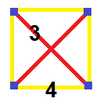Tetragonal disphenoid
Symmetry	[[3,2,3]] = [6,2⁺,6], order 72
Dual	3-3 duopyramid
Properties	convex, vertex-uniform, facet-transitive

In geometry of 4 dimensions, a 3-3 duoprism or triangular duoprism, the smallest p-q duoprism, is a 4-polytope resulting from the Cartesian product of two triangles.

It has 9 vertices, 18 edges, 15 faces (9 squares, and 6 triangles), in 6 triangular prism cells. It has Coxeter diagram , and symmetry [[3,2,3]], order 72. Its vertices and edges form a $3\times 3$ rook's graph.

Hypervolume

The hypervolume of a uniform 3-3 duoprism, with edge length a, is $V_{4}={3 \over 16}a^{4}$ . This is computed as the product of the area of an equilateral triangle squared, $A={{\sqrt {3}} \over 4}a^{2}$ .

Images

Orthogonal projections

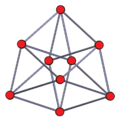
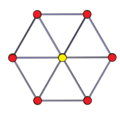
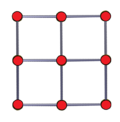
Net	Vertex-centered perspective	3D perspective projection with 2 different rotations

Symmetry

In 5-dimensions, the some uniform 5-polytopes have 3-3 duoprism vertex figures, some with unequal edge-lengths and therefore lower symmetry:

Symmetry	[[3,2,3]], order 72	[3,2], order 12
Coxeter diagram
Schlegel diagram
Name	t₂α₅	t₀₃α₅	t₀₃γ₅	t₀₃β₅

The birectified 16-cell honeycomb also has a 3-3 duoprism vertex figures. There are three constructions for the honeycomb with two lower symmetries.

Symmetry	[3,2,3], order 36	[3,2], order 12	[3], order 6
Coxeter diagram
Skew orthogonal projection

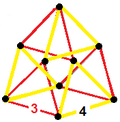
Related complex polygons

The regular complex polytope ₃{4}₂, , in $\mathbb {C} ^{2}$ has a real representation as a 3-3 duoprism in 4-dimensional space. ₃{4}₂ has 9 vertices, and 6 3-edges. Its symmetry is ₃[4]₂, order 18. It also has a lower symmetry construction, , or ₃{}×₃{}, with symmetry ₃[2]₃, order 9. This is the symmetry if the red and blue 3-edges are considered distinct.^[1]

Perspective projection	Orthogonal projection with coinciding central vertices	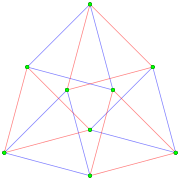Orthogonal projection, offset view to avoid overlapping elements.

Related polytopes

k₂₂ figures in n dimensions
Space	Finite			Euclidean	Hyperbolic
n	4	5	6	7	8
Coxeter group	A₂A₂	E₆	${\tilde {E}}_{6}$ =E₆⁺	${\bar {T}}_{7}$ =E₆⁺⁺
Coxeter diagram
Symmetry	[[3^2,2,-1]]	[[3^2,2,0]]	[[3^2,2,1]]	[[3^2,2,2]]	[[3^2,2,3]]
Order	72	1440	103,680	∞
Graph				∞	∞
Name	−1₂₂	0₂₂	1₂₂	2₂₂	3₂₂

3-3 duopyramid

3-3 duopyramid
Type	Uniform dual duopyramid
Schläfli symbol	{3}+{3} = 2{3}
Coxeter diagram
Cells	9 tetragonal disphenoids
Faces	18 isosceles triangles
Edges	15 (9+6)
Vertices	6 (3+3)
Symmetry	[[3,2,3]] = [6,2⁺,6], order 72
Dual	3-3 duoprism
Properties	convex, vertex-uniform, facet-transitive

The dual of a 3-3 duoprism is called a 3-3 duopyramid or triangular duopyramid. It has 9 tetragonal disphenoid cells, 18 triangular faces, 15 edges, and 6 vertices.

It can be seen in orthogonal projection as a 6-gon circle of vertices, and edges connecting all pairs, just like a 5-simplex seen in projection.

orthogonal projection

Related complex polygon

The regular complex polygon ₂{4}₃ has 6 vertices in $\mathbb {C} ^{2}$ with a real representation in $\mathbb {R} ^{4}$ matching the same vertex arrangement of the 3-3 duopyramid. It has 9 2-edges corresponding to the connecting edges of the 3-3 duopyramid, while the 6 edges connecting the two triangles are not included. It can be seen in a hexagonal projection with 3 sets of colored edges. This arrangement of vertices and edges makes a complete bipartite graph with each vertex from one triangle is connected to every vertex on the other. It is also called a Thomsen graph or 4-cage.^[2]

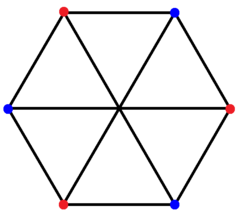The ₂{4}₃ with 6 vertices in blue and red connected by 9 2-edges as a complete bipartite graph.	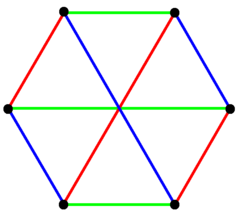It has 3 sets of 3 edges, seen here with colors.

Notes

^ Coxeter, H. S. M.; Regular Complex Polytopes, Cambridge University Press, (1974).
^ Regular Complex Polytopes, p.110, p.114

References

Regular Polytopes, H. S. M. Coxeter, Dover Publications, Inc., 1973, New York, p. 124.
Coxeter, The Beauty of Geometry: Twelve Essays, Dover Publications, 1999, ISBN 0-486-40919-8 (Chapter 5: Regular Skew Polyhedra in three and four dimensions and their topological analogues)
- Coxeter, H. S. M. Regular Skew Polyhedra in Three and Four Dimensions. Proc. London Math. Soc. 43, 33-62, 1937.
John H. Conway, Heidi Burgiel, Chaim Goodman-Strass, The Symmetries of Things 2008, ISBN 978-1-56881-220-5 (Chapter 26)
Norman Johnson Uniform Polytopes, Manuscript (1991)
- N.W. Johnson: The Theory of Uniform Polytopes and Honeycombs, Ph.D. Dissertation, University of Toronto, 1966
Catalogue of Convex Polychora, section 6, George Olshevsky.
Apollonian Ball Packings and Stacked Polytopes Discrete & Computational Geometry, June 2016, Volume 55, Issue 4, pp 801–826

External links

The Fourth Dimension Simply Explained—describes duoprisms as "double prisms" and duocylinders as "double cylinders"
Polygloss – glossary of higher-dimensional terms
Exploring Hyperspace with the Geometric Product

[1] Coxeter, H. S. M.; Regular Complex Polytopes, Cambridge University Press, (1974).

[2] Regular Complex Polytopes, p.110, p.114

[1]

[2]