Small snub icosicosidodecahedron
| Small snub icosicosidodecahedron | |
|---|---|
| |
| Type | Uniform star polyhedron |
| Elements | F = 112, E = 180 V = 60 (χ = −8) |
| Faces by sides | (40+60){3}+12{5/2} |
| Coxeter diagram |    
|
| Wythoff symbol | | 5/2 3 3 |
| Symmetry group | Ih, [5,3], *532 |
| Index references | U32, C41, W110 |
| Dual polyhedron | Small hexagonal hexecontahedron |
| Vertex figure |  35.5/2 |
| Bowers acronym | Seside |
In geometry, the small snub icosicosidodecahedron or snub disicosidodecahedron is a uniform star polyhedron, indexed as U32. It has 112 faces (100 triangles and 12 pentagrams), 180 edges, and 60 vertices. Its stellation core is a truncated pentakis dodecahedron. It also called a holosnub icosahedron, ß{3,5}.
The 40 non-snub triangular faces form 20 coplanar pairs, forming star hexagons that are not quite regular. Unlike most snub polyhedra, it has reflection symmetries.
Convex hull
Its convex hull is a nonuniform truncated icosahedron.
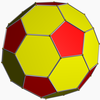 Truncated icosahedron (regular faces) |
 Convex hull (isogonal hexagons) |
Small snub icosicosidodecahedron |
Cartesian coordinates
Cartesian coordinates for the vertices of a small snub icosicosidodecahedron are all the even permutations of
- (±(1-ϕ+α), 0, ±(3+ϕα))
- (±(ϕ-1+α), ±2, ±(2ϕ-1+ϕα))
- (±(ϕ+1+α), ±2(ϕ-1), ±(1+ϕα))
where ϕ = (1+√5)/2 is the golden ratio and α = √3ϕ−2.
See also
External links
- Weisstein, Eric W. "Small snub icosicosidodecahedron". MathWorld.
- Klitzing, Richard. "3D star small snub icosicosidodecahedron".
 | This polyhedron-related article is a stub. You can help Wikipedia by expanding it. |