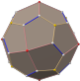
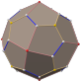
Truncated icosahedron
| Truncated icosahedron | |
|---|---|
 (Click here for rotating model) | |
| Type | Archimedean solid Uniform polyhedron |
| Elements | F = 32, E = 90, V = 60 (χ = 2) |
| Faces by sides | 12{5}+20{6} |
| Conway notation | tI |
| Schläfli symbols | t{3,5} |
| t0,1{3,5} | |
| Wythoff symbol | 2 5 | 3 |
| Coxeter diagram | |
| Symmetry group | Ih, H3, [5,3], (*532), order 120 |
| Rotation group | I, [5,3]+, (532), order 60 |
| Dihedral angle | 6-6: 138.189685° 6-5: 142.62° |
| References | U25, C27, W9 |
| Properties | Semiregular convex |
 Colored faces |
 5.6.6 (Vertex figure) |
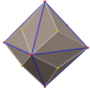
 Pentakis dodecahedron (dual polyhedron) |
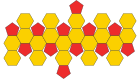 Net |
In geometry, the truncated icosahedron is an Archimedean solid, one of 13 convex isogonal nonprismatic solids whose 32 faces are two or more types of regular polygons. It is the only one of these shapes that does not contain triangles or squares. In general usage, the degree of truncation is assumed to be uniform unless specified.
It has 12 regular pentagonal faces, 20 regular hexagonal faces, 60 vertices and 90 edges.
It is the Goldberg polyhedron GPV(1,1) or {5+,3}1,1, containing pentagonal and hexagonal faces.
This geometry is associated with footballs (soccer balls) typically patterned with white hexagons and black pentagons. Geodesic domes such as those whose architecture Buckminster Fuller pioneered are often based on this structure. It also corresponds to the geometry of the fullerene C60 ("buckyball") molecule.
It is used in the cell-transitive hyperbolic space-filling tessellation, the bitruncated order-5 dodecahedral honeycomb.
Construction[edit]

This polyhedron can be constructed from an icosahedron by truncating, or cutting off, each of the 12 vertices at the one-third mark of each edge, creating 12 pentagonal faces and transforming the original 20 triangle faces into regular hexagons.[1][2]
Characteristics[edit]
In geometry and graph theory, there are some standard polyhedron characteristics.
Cartesian coordinates[edit]
Cartesian coordinates for the vertices of a truncated icosahedron centered at the origin are all even permutations of:
where is the golden mean. The circumradius is and the edges have length 2.[3]
Orthogonal projections[edit]
The truncated icosahedron has five special orthogonal projections, centered, on a vertex, on two types of edges, and two types of faces: hexagonal and pentagonal. The last two correspond to the A2 and H2 Coxeter planes.
| Centered by | Vertex | Edge 5-6 |
Edge 6-6 |
Face Hexagon |
Face Pentagon |
|---|---|---|---|---|---|
| Solid | 
|

|

| ||
| Wireframe | 
|
|
|
|

|
| Projective symmetry |
[2] | [2] | [2] | [6] | [10] |
| Dual | 
|
|

|
|

|
Spherical tiling[edit]
The truncated icosahedron can also be represented as a spherical tiling, and projected onto the plane via a stereographic projection. This projection is conformal, preserving angles but not areas or lengths. Straight lines on the sphere are projected as circular arcs on the plane.

|
 pentagon-centered |
 hexagon-centered |
| Orthographic projection | Stereographic projections | |
|---|---|---|
Dimensions[edit]

If the edge length of a truncated icosahedron is a, the radius of a circumscribed sphere (one that touches the truncated icosahedron at all vertices) is:
where φ is the golden ratio.
This result is easy to get by using one of the three orthogonal golden rectangles drawn into the original icosahedron (before cut off) as the starting point for our considerations. The angle between the segments joining the center and the vertices connected by shared edge (calculated on the basis of this construction) is approximately 23.281446°.
Area and volume[edit]
The area A and the volume V of the truncated icosahedron of edge length a[4] are:
Applications[edit]
The balls used in association football and team handball are perhaps the best-known example of a spherical polyhedron analog to the truncated icosahedron, found in everyday life.[5] The ball comprises the same pattern of regular pentagons and regular hexagons, but it is more spherical due to the pressure of the air inside and the elasticity of the ball. This ball type was introduced to the World Cup in 1970 (starting in 2006, this iconic design has been superseded by alternative patterns).
Geodesic domes are typically based on triangular facetings of this geometry with example structures found across the world, popularized by Buckminster Fuller.[6]
This shape was also the configuration of the lenses used for focusing the explosive shock waves of the detonators in both the gadget and Fat Man atomic bombs.[7]
The truncated icosahedron can also be described as a model of the Buckminsterfullerene (fullerene) (C60), or "buckyball", molecule – an allotrope of elemental carbon, discovered in 1985. The diameter of the football and the fullerene molecule are 22 cm and about 0.71 nm, respectively, hence the size ratio is ≈31,000,000:1.
In popular craft culture, large sparkleballs can be made using a icosahedron pattern and plastic, styrofoam or paper cups.
In the arts[edit]
- Gallery
-
The truncated icosahedron (left) compared with an association football.
-
Fullerene C60 molecule
-
Truncated icosahedral radome on a weather station
-
Truncated icosahedron machined out of 6061-T6 aluminum
-
A wooden truncated icosahedron artwork by George W. Hart.
Related polyhedra[edit]
| Family of uniform icosahedral polyhedra | |||||||
|---|---|---|---|---|---|---|---|
| Symmetry: [5,3], (*532) | [5,3]+, (532) | ||||||

|

|

|

|

|

|

|

|
| {5,3} | t{5,3} | r{5,3} | t{3,5} | {3,5} | rr{5,3} | tr{5,3} | sr{5,3} |
| Duals to uniform polyhedra | |||||||

|

|

|

|

|

| ||
| V5.5.5 | V3.10.10 | V3.5.3.5 | V5.6.6 | V3.3.3.3.3 | V3.4.5.4 | V4.6.10 | V3.3.3.3.5 |
| *n32 symmetry mutation of truncated tilings: n.6.6 | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Sym. *n42 [n,3] |
Spherical | Euclid. | Compact | Parac. | Noncompact hyperbolic | |||||||
| *232 [2,3] |
*332 [3,3] |
*432 [4,3] |
*532 [5,3] |
*632 [6,3] |
*732 [7,3] |
*832 [8,3]... |
*∞32 [∞,3] |
[12i,3] | [9i,3] | [6i,3] | ||
| Truncated figures |

|

|

|

|

|

|

|

|

|

|

| |
| Config. | 2.6.6 | 3.6.6 | 4.6.6 | 5.6.6 | 6.6.6 | 7.6.6 | 8.6.6 | ∞.6.6 | 12i.6.6 | 9i.6.6 | 6i.6.6 | |
| n-kis figures |

|

|

|

|

|

|

|

|
||||
| Config. | V2.6.6 | V3.6.6 | V4.6.6 | V5.6.6 | V6.6.6 | V7.6.6 | V8.6.6 | V∞.6.6 | V12i.6.6 | V9i.6.6 | V6i.6.6 | |
These uniform star-polyhedra, and one icosahedral stellation have nonuniform truncated icosahedra convex hulls:
| Uniform star polyhedra with truncated icosahedra convex hulls | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
This polyhedron looks similar to the uniform chamfered dodecahedron which has 12 pentagons, but 30 hexagons.
Truncated icosahedral graph[edit]
| Truncated icosahedral graph | |
|---|---|
 6-fold symmetry schlegel diagram | |
| Vertices | 60 |
| Edges | 90 |
| Automorphisms | 120 |
| Chromatic number | 3 |
| Properties | Cubic, Hamiltonian, regular, zero-symmetric |
| Table of graphs and parameters | |
In the mathematical field of graph theory, a truncated icosahedral graph is the graph of vertices and edges of the truncated icosahedron, one of the Archimedean solids. It has 60 vertices and 90 edges, and is a cubic Archimedean graph.[8][9][10]
 5-fold symmetry |
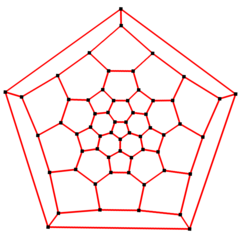 5-fold Schlegel diagram |
History[edit]

The truncated icosahedron was known to Archimedes, who classified the 13 Archimedean solids in a lost work. All we know of his work on these shapes comes from Pappus of Alexandria, who merely lists the numbers of faces for each: 12 pentagons and 20 hexagons, in the case of the truncated icosahedron. The first known image and complete description of a truncated icosahedron is from a rediscovery by Piero della Francesca, in his 15th-century book De quinque corporibus regularibus,[11] which included five of the Archimedean solids (the five truncations of the regular polyhedra). The same shape was depicted by Leonardo da Vinci, in his illustrations for Luca Pacioli's plagiarism of della Francesca's book in 1509. Although Albrecht Dürer omitted this shape from the other Archimedean solids listed in his 1525 book on polyhedra, Underweysung der Messung, a description of it was found in his posthumous papers, published in 1538. Johannes Kepler later rediscovered the complete list of the 13 Archimedean solids, including the truncated icosahedron, and included them in his 1609 book, Harmonices Mundi.[12]
See also[edit]
Notes[edit]
- ^ Mednikov, Evgueni G.; Jewell, Matthew C.; Dahl, Lawrence F. (2007-09-01). "Nanosized (μ 12 -Pt)Pd 164- x Pt x (CO) 72 (PPh 3 ) 20 ( x ≈ 7) Containing Pt-Centered Four-Shell 165-Atom Pd−Pt Core with Unprecedented Intershell Bridging Carbonyl Ligands: Comparative Analysis of Icosahedral Shell-Growth Patterns with Geometrically Related Pd 145 (CO) x (PEt 3 ) 30 ( x ≈ 60) Containing Capped Three-Shell Pd 145 Core". Journal of the American Chemical Society. 129 (37): 11624. doi:10.1021/ja073945q. ISSN 0002-7863. PMID 17722929.
- ^ Kotschick, Dieter (July–August 2006). "The Topology and Combinatorics of Soccer Balls". American Scientist. 94 (4): 350. doi:10.1511/2006.60.350.
- ^ Weisstein, Eric W. "Icosahedral group". MathWorld.
- ^ Weisstein, Eric W. "Truncated Icosahedron". mathworld.wolfram.com. Retrieved 2023-09-10.
- ^ Kotschick, Dieter (2006). "The Topology and Combinatorics of Soccer Balls". American Scientist. 94 (4): 350–357. doi:10.1511/2006.60.350.
- ^ Krebs, Albin (July 2, 1983). "R. Buckminster Fuller Dead; Futurist Built Geodesic Dome". The New York Times. New York, N.Y. p. 1. Retrieved 7 November 2021.
- ^ Rhodes, Richard (1996). Dark Sun: The Making of the Hydrogen Bomb. Touchstone Books. pp. 195. ISBN 0-684-82414-0.
- ^ Read, R. C.; Wilson, R. J. (1998). An Atlas of Graphs. Oxford University Press. p. 268.
- ^ Godsil, C. and Royle, G. Algebraic Graph Theory New York: Springer-Verlag, p. 211, 2001
- ^ Kostant, B. The Graph of the Truncated Icosahedron and the Last Letter of Galois. Notices Amer. Math. Soc. 42, 1995, pp. 959-968 PDF
- ^ Katz, Eugene A. (2011). "Bridges between mathematics, natural sciences, architecture and art: case of fullerenes". Art, Science, and Technology: Interaction Between Three Cultures, Proceedings of the First International Conference. pp. 60–71.
- ^ Field, J. V. (1997). "Rediscovering the Archimedean polyhedra: Piero della Francesca, Luca Pacioli, Leonardo da Vinci, Albrecht Dürer, Daniele Barbaro, and Johannes Kepler". Archive for History of Exact Sciences. 50 (3–4): 241–289. doi:10.1007/BF00374595. JSTOR 41134110. MR 1457069. S2CID 118516740.
References[edit]
- Williams, Robert (1979). The Geometrical Foundation of Natural Structure: A Source Book of Design. Dover Publications, Inc. ISBN 0-486-23729-X. (Section 3-9)
- Cromwell, P. (1997). "Archimedean solids". Polyhedra: "One of the Most Charming Chapters of Geometry". Cambridge: Cambridge University Press. pp. 79–86. ISBN 0-521-55432-2. OCLC 180091468.
External links[edit]
- Weisstein, Eric W., "Truncated icosahedron" ("Archimedean solid") at MathWorld.
- Klitzing, Richard. "3D convex uniform polyhedra x3x5o - ti".
- Editable printable net of a truncated icosahedron with interactive 3D view
- The Uniform Polyhedra
- "Virtual Reality Polyhedra"—The Encyclopedia of Polyhedra
- 3D paper data visualization World Cup ball

![{\displaystyle {\begin{alignedat}{5}{\Bigl (}&&0,&&\pm \,1,&&\pm \,3\varphi {\Bigr )},\\[2pt]{\Bigl (}&&\pm \,1,&&\quad \pm \,(2+\varphi ),&&\pm \,2\varphi {\Bigr )},\\[2pt]{\Bigl (}&&\pm \,\varphi ,&&\pm \,2,&&\quad \pm \,(2\varphi +1){\Bigr )},\end{alignedat}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/23246fa2e710bc39e22b4b5438ea081efe7e2c0b)