Great duoantiprism
| Great duoantiprism | |
|---|---|
| Type | Uniform polychoron |
| Schläfli symbols | s{5}s{5/3} {5}⊗{5/3} h{10}s{5/3} s{5}h{10/3} h{10}h{10/3} |
| Coxeter diagrams | |
| Cells | 50 tetrahedra 10 pentagonal antiprisms 10 pentagrammic crossed-antiprisms |
| Faces | 200 triangles 10 pentagons 10 pentagrams |
| Edges | 200 |
| Vertices | 50 |
| Vertex figure | 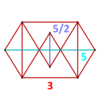 star-gyrobifastigium |
| Symmetry group | [5,2,5]+, order 50 [(5,2)+,10], order 100 [10,2+,10], order 200 |
| Properties | Vertex-uniform |
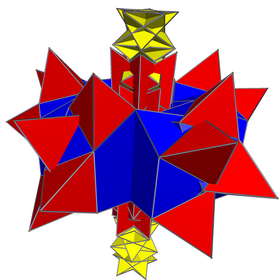 Net (overlapping in space) | |
In geometry, the great duoantiprism is the only uniform star-duoantiprism solution p = 5, q = 5/3, in 4-dimensional geometry. It has Schläfli symbol {5}⊗{5/3}, s{5}s{5/3} or ht0,1,2,3{5,2,5/3}, Coxeter diagram ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() , constructed from 10 pentagonal antiprisms, 10 pentagrammic crossed-antiprisms, and 50 tetrahedra.
, constructed from 10 pentagonal antiprisms, 10 pentagrammic crossed-antiprisms, and 50 tetrahedra.
Its vertices are a subset of those of the small stellated 120-cell.
Construction
The great duoantiprism can be constructed from a nonuniform variant of the 10-10/3 duoprism (a duoprism of a decagon and a decagram) where the decagram's edge length is around 1.618 (golden ratio) times the edge length of the decagon via an alternation process. The decagonal prisms alternate into pentagonal antiprisms, the decagrammic prisms alternate into pentagrammic crossed-antiprisms with new regular tetrahedra created at the deleted vertices. This is the only uniform solution for the p-q duoantiprism aside from the regular 16-cell (as a 2-2 duoantiprism).
Images
 stereographic projection, centered on one pentagrammic crossed-antiprism |
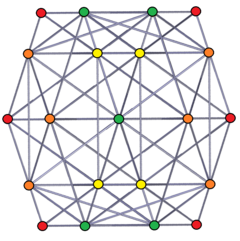 Orthogonal projection, with vertices colored by overlaps, red, orange, yellow, green have 1, 2, 3,4 multiplicity. |
Other names
References
- ^ Jonathan Bowers - Miscellaneous Uniform Polychora 965. Gudap
- ^ http://www.polychora.com/12GudapsMovie.gif Animation of cross sections
- Regular Polytopes, H. S. M. Coxeter, Dover Publications, Inc., 1973, New York, p. 124.
- Norman Johnson Uniform Polytopes, Manuscript (1991)
- N.W. Johnson: The Theory of Uniform Polytopes and Honeycombs, Ph.D. Dissertation, University of Toronto, 1966
- Klitzing, Richard. "4D uniform polytopes (polychora) s5/3s2s5s - gudap".
