In continuum mechanics , the most commonly used measure of stress is the Cauchy stress tensor , often called simply the stress tensor or "true stress". However, several alternative measures of stress can be defined:[ 1] [ 2] [ 3]
The Kirchhoff stress (
τ
{\displaystyle {\boldsymbol {\tau }}}
The nominal stress (
N
{\displaystyle {\boldsymbol {N}}}
The Piola–Kirchhoff stress tensors
The first Piola–Kirchhoff stress (
P
{\displaystyle {\boldsymbol {P}}}
P
=
N
T
{\displaystyle {\boldsymbol {P}}={\boldsymbol {N}}^{T}}
The second Piola–Kirchhoff stress or PK2 stress (
S
{\displaystyle {\boldsymbol {S}}}
The Biot stress (
T
{\displaystyle {\boldsymbol {T}}}
Consider the situation shown in the following figure. The following definitions use the notations shown in the figure.
Quantities used in the definition of stress measures
In the reference configuration
Ω
0
{\displaystyle \Omega _{0}}
d
Γ
0
{\displaystyle d\Gamma _{0}}
N
≡
n
0
{\displaystyle \mathbf {N} \equiv \mathbf {n} _{0}}
t
0
{\displaystyle \mathbf {t} _{0}}
d
f
0
{\displaystyle d\mathbf {f} _{0}}
Ω
{\displaystyle \Omega }
d
Γ
{\displaystyle d\Gamma }
n
{\displaystyle \mathbf {n} }
t
{\displaystyle \mathbf {t} }
d
f
{\displaystyle d\mathbf {f} }
F
{\displaystyle {\boldsymbol {F}}}
deformation gradient tensor ,
J
{\displaystyle J}
The Cauchy stress (or true stress) is a measure of the force acting on an element of area in the deformed configuration. This tensor is symmetric and is defined via
d
f
=
t
d
Γ
=
σ
T
⋅
n
d
Γ
{\displaystyle d\mathbf {f} =\mathbf {t} ~d\Gamma ={\boldsymbol {\sigma }}^{T}\cdot \mathbf {n} ~d\Gamma }
or
t
=
σ
T
⋅
n
{\displaystyle \mathbf {t} ={\boldsymbol {\sigma }}^{T}\cdot \mathbf {n} }
where
t
{\displaystyle \mathbf {t} }
n
{\displaystyle \mathbf {n} }
The quantity,
τ
=
J
σ
{\displaystyle {\boldsymbol {\tau }}=J~{\boldsymbol {\sigma }}}
is called the Kirchhoff stress tensor , with
J
{\displaystyle J}
F
{\displaystyle {\boldsymbol {F}}}
weighted Cauchy stress tensor as well.
[ edit ] [ edit ] The nominal stress
N
=
P
T
{\displaystyle {\boldsymbol {N}}={\boldsymbol {P}}^{T}}
P
{\displaystyle {\boldsymbol {P}}}
d
f
=
t
d
Γ
=
N
T
⋅
n
0
d
Γ
0
=
P
⋅
n
0
d
Γ
0
{\displaystyle d\mathbf {f} =\mathbf {t} ~d\Gamma ={\boldsymbol {N}}^{T}\cdot \mathbf {n} _{0}~d\Gamma _{0}={\boldsymbol {P}}\cdot \mathbf {n} _{0}~d\Gamma _{0}}
or
t
0
=
t
d
Γ
d
Γ
0
=
N
T
⋅
n
0
=
P
⋅
n
0
{\displaystyle \mathbf {t} _{0}=\mathbf {t} {\dfrac {d{\Gamma }}{d\Gamma _{0}}}={\boldsymbol {N}}^{T}\cdot \mathbf {n} _{0}={\boldsymbol {P}}\cdot \mathbf {n} _{0}}
This stress is unsymmetric and is a two-point tensor like the deformation gradient.[ 4]
[ edit ] If we pull back
d
f
{\displaystyle d\mathbf {f} }
d
f
0
{\displaystyle d\mathbf {f} _{0}}
d
f
0
=
F
−
1
⋅
d
f
{\displaystyle d\mathbf {f} _{0}={\boldsymbol {F}}^{-1}\cdot d\mathbf {f} }
or,
d
f
0
=
F
−
1
⋅
N
T
⋅
n
0
d
Γ
0
=
F
−
1
⋅
t
0
d
Γ
0
{\displaystyle d\mathbf {f} _{0}={\boldsymbol {F}}^{-1}\cdot {\boldsymbol {N}}^{T}\cdot \mathbf {n} _{0}~d\Gamma _{0}={\boldsymbol {F}}^{-1}\cdot \mathbf {t} _{0}~d\Gamma _{0}}
The PK2 stress (
S
{\displaystyle {\boldsymbol {S}}}
d
f
0
=
S
T
⋅
n
0
d
Γ
0
=
F
−
1
⋅
t
0
d
Γ
0
{\displaystyle d\mathbf {f} _{0}={\boldsymbol {S}}^{T}\cdot \mathbf {n} _{0}~d\Gamma _{0}={\boldsymbol {F}}^{-1}\cdot \mathbf {t} _{0}~d\Gamma _{0}}
Therefore,
S
T
⋅
n
0
=
F
−
1
⋅
t
0
{\displaystyle {\boldsymbol {S}}^{T}\cdot \mathbf {n} _{0}={\boldsymbol {F}}^{-1}\cdot \mathbf {t} _{0}}
The Biot stress is useful because it is energy conjugate to the right stretch tensor
U
{\displaystyle {\boldsymbol {U}}}
P
T
⋅
R
{\displaystyle {\boldsymbol {P}}^{T}\cdot {\boldsymbol {R}}}
R
{\displaystyle {\boldsymbol {R}}}
polar decomposition of the deformation gradient. Therefore, the Biot stress tensor is defined as
T
=
1
2
(
R
T
⋅
P
+
P
T
⋅
R
)
.
{\displaystyle {\boldsymbol {T}}={\tfrac {1}{2}}({\boldsymbol {R}}^{T}\cdot {\boldsymbol {P}}+{\boldsymbol {P}}^{T}\cdot {\boldsymbol {R}})~.}
The Biot stress is also called the Jaumann stress.
The quantity
T
{\displaystyle {\boldsymbol {T}}}
R
T
d
f
=
(
P
T
⋅
R
)
T
⋅
n
0
d
Γ
0
{\displaystyle {\boldsymbol {R}}^{T}~d\mathbf {f} =({\boldsymbol {P}}^{T}\cdot {\boldsymbol {R}})^{T}\cdot \mathbf {n} _{0}~d\Gamma _{0}}
Relations between Cauchy stress and nominal stress [ edit ] From Nanson's formula relating areas in the reference and deformed configurations:
n
d
Γ
=
J
F
−
T
⋅
n
0
d
Γ
0
{\displaystyle \mathbf {n} ~d\Gamma =J~{\boldsymbol {F}}^{-T}\cdot \mathbf {n} _{0}~d\Gamma _{0}}
Now,
σ
T
⋅
n
d
Γ
=
d
f
=
N
T
⋅
n
0
d
Γ
0
{\displaystyle {\boldsymbol {\sigma }}^{T}\cdot \mathbf {n} ~d\Gamma =d\mathbf {f} ={\boldsymbol {N}}^{T}\cdot \mathbf {n} _{0}~d\Gamma _{0}}
Hence,
σ
T
⋅
(
J
F
−
T
⋅
n
0
d
Γ
0
)
=
N
T
⋅
n
0
d
Γ
0
{\displaystyle {\boldsymbol {\sigma }}^{T}\cdot (J~{\boldsymbol {F}}^{-T}\cdot \mathbf {n} _{0}~d\Gamma _{0})={\boldsymbol {N}}^{T}\cdot \mathbf {n} _{0}~d\Gamma _{0}}
or,
N
T
=
J
(
F
−
1
⋅
σ
)
T
=
J
σ
T
⋅
F
−
T
{\displaystyle {\boldsymbol {N}}^{T}=J~({\boldsymbol {F}}^{-1}\cdot {\boldsymbol {\sigma }})^{T}=J~{\boldsymbol {\sigma }}^{T}\cdot {\boldsymbol {F}}^{-T}}
or,
N
=
J
F
−
1
⋅
σ
and
N
T
=
P
=
J
σ
T
⋅
F
−
T
{\displaystyle {\boldsymbol {N}}=J~{\boldsymbol {F}}^{-1}\cdot {\boldsymbol {\sigma }}\qquad {\text{and}}\qquad {\boldsymbol {N}}^{T}={\boldsymbol {P}}=J~{\boldsymbol {\sigma }}^{T}\cdot {\boldsymbol {F}}^{-T}}
In index notation,
N
I
j
=
J
F
I
k
−
1
σ
k
j
and
P
i
J
=
J
σ
k
i
F
J
k
−
1
{\displaystyle N_{Ij}=J~F_{Ik}^{-1}~\sigma _{kj}\qquad {\text{and}}\qquad P_{iJ}=J~\sigma _{ki}~F_{Jk}^{-1}}
Therefore,
J
σ
=
F
⋅
N
=
F
⋅
P
T
.
{\displaystyle J~{\boldsymbol {\sigma }}={\boldsymbol {F}}\cdot {\boldsymbol {N}}={\boldsymbol {F}}\cdot {\boldsymbol {P}}^{T}~.}
Note that
N
{\displaystyle {\boldsymbol {N}}}
P
{\displaystyle {\boldsymbol {P}}}
F
{\displaystyle {\boldsymbol {F}}}
[ edit ] Recall that
N
T
⋅
n
0
d
Γ
0
=
d
f
{\displaystyle {\boldsymbol {N}}^{T}\cdot \mathbf {n} _{0}~d\Gamma _{0}=d\mathbf {f} }
and
d
f
=
F
⋅
d
f
0
=
F
⋅
(
S
T
⋅
n
0
d
Γ
0
)
{\displaystyle d\mathbf {f} ={\boldsymbol {F}}\cdot d\mathbf {f} _{0}={\boldsymbol {F}}\cdot ({\boldsymbol {S}}^{T}\cdot \mathbf {n} _{0}~d\Gamma _{0})}
Therefore,
N
T
⋅
n
0
=
F
⋅
S
T
⋅
n
0
{\displaystyle {\boldsymbol {N}}^{T}\cdot \mathbf {n} _{0}={\boldsymbol {F}}\cdot {\boldsymbol {S}}^{T}\cdot \mathbf {n} _{0}}
or (using the symmetry of
S
{\displaystyle {\boldsymbol {S}}}
N
=
S
⋅
F
T
and
P
=
F
⋅
S
{\displaystyle {\boldsymbol {N}}={\boldsymbol {S}}\cdot {\boldsymbol {F}}^{T}\qquad {\text{and}}\qquad {\boldsymbol {P}}={\boldsymbol {F}}\cdot {\boldsymbol {S}}}
In index notation,
N
I
j
=
S
I
K
F
j
K
T
and
P
i
J
=
F
i
K
S
K
J
{\displaystyle N_{Ij}=S_{IK}~F_{jK}^{T}\qquad {\text{and}}\qquad P_{iJ}=F_{iK}~S_{KJ}}
Alternatively, we can write
S
=
N
⋅
F
−
T
and
S
=
F
−
1
⋅
P
{\displaystyle {\boldsymbol {S}}={\boldsymbol {N}}\cdot {\boldsymbol {F}}^{-T}\qquad {\text{and}}\qquad {\boldsymbol {S}}={\boldsymbol {F}}^{-1}\cdot {\boldsymbol {P}}}
[ edit ] Recall that
N
=
J
F
−
1
⋅
σ
{\displaystyle {\boldsymbol {N}}=J~{\boldsymbol {F}}^{-1}\cdot {\boldsymbol {\sigma }}}
In terms of the 2nd PK stress, we have
S
⋅
F
T
=
J
F
−
1
⋅
σ
{\displaystyle {\boldsymbol {S}}\cdot {\boldsymbol {F}}^{T}=J~{\boldsymbol {F}}^{-1}\cdot {\boldsymbol {\sigma }}}
Therefore,
S
=
J
F
−
1
⋅
σ
⋅
F
−
T
=
F
−
1
⋅
τ
⋅
F
−
T
{\displaystyle {\boldsymbol {S}}=J~{\boldsymbol {F}}^{-1}\cdot {\boldsymbol {\sigma }}\cdot {\boldsymbol {F}}^{-T}={\boldsymbol {F}}^{-1}\cdot {\boldsymbol {\tau }}\cdot {\boldsymbol {F}}^{-T}}
In index notation,
S
I
J
=
F
I
k
−
1
τ
k
l
F
J
l
−
1
{\displaystyle S_{IJ}=F_{Ik}^{-1}~\tau _{kl}~F_{Jl}^{-1}}
Since the Cauchy stress (and hence the Kirchhoff stress) is symmetric, the 2nd PK stress is also symmetric.
Alternatively, we can write
σ
=
J
−
1
F
⋅
S
⋅
F
T
{\displaystyle {\boldsymbol {\sigma }}=J^{-1}~{\boldsymbol {F}}\cdot {\boldsymbol {S}}\cdot {\boldsymbol {F}}^{T}}
or,
τ
=
F
⋅
S
⋅
F
T
.
{\displaystyle {\boldsymbol {\tau }}={\boldsymbol {F}}\cdot {\boldsymbol {S}}\cdot {\boldsymbol {F}}^{T}~.}
Clearly, from definition of the push-forward and pull-back operations, we have
S
=
φ
∗
[
τ
]
=
F
−
1
⋅
τ
⋅
F
−
T
{\displaystyle {\boldsymbol {S}}=\varphi ^{*}[{\boldsymbol {\tau }}]={\boldsymbol {F}}^{-1}\cdot {\boldsymbol {\tau }}\cdot {\boldsymbol {F}}^{-T}}
and
τ
=
φ
∗
[
S
]
=
F
⋅
S
⋅
F
T
.
{\displaystyle {\boldsymbol {\tau }}=\varphi _{*}[{\boldsymbol {S}}]={\boldsymbol {F}}\cdot {\boldsymbol {S}}\cdot {\boldsymbol {F}}^{T}~.}
Therefore,
S
{\displaystyle {\boldsymbol {S}}}
τ
{\displaystyle {\boldsymbol {\tau }}}
F
{\displaystyle {\boldsymbol {F}}}
τ
{\displaystyle {\boldsymbol {\tau }}}
S
{\displaystyle {\boldsymbol {S}}}
Key:
J
=
det
(
F
)
,
C
=
F
T
F
=
U
2
,
F
=
R
U
,
R
T
=
R
−
1
,
{\displaystyle J=\det \left({\boldsymbol {F}}\right),\quad {\boldsymbol {C}}={\boldsymbol {F}}^{T}{\boldsymbol {F}}={\boldsymbol {U}}^{2},\quad {\boldsymbol {F}}={\boldsymbol {R}}{\boldsymbol {U}},\quad {\boldsymbol {R}}^{T}={\boldsymbol {R}}^{-1},}
P
=
J
σ
F
−
T
,
τ
=
J
σ
,
S
=
J
F
−
1
σ
F
−
T
,
T
=
R
T
P
,
M
=
C
S
{\displaystyle {\boldsymbol {P}}=J{\boldsymbol {\sigma }}{\boldsymbol {F}}^{-T},\quad {\boldsymbol {\tau }}=J{\boldsymbol {\sigma }},\quad {\boldsymbol {S}}=J{\boldsymbol {F}}^{-1}{\boldsymbol {\sigma }}{\boldsymbol {F}}^{-T},\quad {\boldsymbol {T}}={\boldsymbol {R}}^{T}{\boldsymbol {P}},\quad {\boldsymbol {M}}={\boldsymbol {C}}{\boldsymbol {S}}}
Conversion formulae
Equation for
σ
{\displaystyle {\boldsymbol {\sigma }}}
τ
{\displaystyle {\boldsymbol {\tau }}}
P
{\displaystyle {\boldsymbol {P}}}
S
{\displaystyle {\boldsymbol {S}}}
T
{\displaystyle {\boldsymbol {T}}}
M
{\displaystyle {\boldsymbol {M}}}
σ
=
{\displaystyle {\boldsymbol {\sigma }}=\,}
σ
{\displaystyle {\boldsymbol {\sigma }}}
J
−
1
τ
{\displaystyle J^{-1}{\boldsymbol {\tau }}}
J
−
1
P
F
T
{\displaystyle J^{-1}{\boldsymbol {P}}{\boldsymbol {F}}^{T}}
J
−
1
F
S
F
T
{\displaystyle J^{-1}{\boldsymbol {F}}{\boldsymbol {S}}{\boldsymbol {F}}^{T}}
J
−
1
R
T
F
T
{\displaystyle J^{-1}{\boldsymbol {R}}{\boldsymbol {T}}{\boldsymbol {F}}^{T}}
J
−
1
F
−
T
M
F
T
{\displaystyle J^{-1}{\boldsymbol {F}}^{-T}{\boldsymbol {M}}{\boldsymbol {F}}^{T}}
τ
=
{\displaystyle {\boldsymbol {\tau }}=\,}
J
σ
{\displaystyle J{\boldsymbol {\sigma }}}
τ
{\displaystyle {\boldsymbol {\tau }}}
P
F
T
{\displaystyle {\boldsymbol {P}}{\boldsymbol {F}}^{T}}
F
S
F
T
{\displaystyle {\boldsymbol {F}}{\boldsymbol {S}}{\boldsymbol {F}}^{T}}
R
T
F
T
{\displaystyle {\boldsymbol {R}}{\boldsymbol {T}}{\boldsymbol {F}}^{T}}
F
−
T
M
F
T
{\displaystyle {\boldsymbol {F}}^{-T}{\boldsymbol {M}}{\boldsymbol {F}}^{T}}
P
=
{\displaystyle {\boldsymbol {P}}=\,}
J
σ
F
−
T
{\displaystyle J{\boldsymbol {\sigma }}{\boldsymbol {F}}^{-T}}
τ
F
−
T
{\displaystyle {\boldsymbol {\tau }}{\boldsymbol {F}}^{-T}}
P
{\displaystyle {\boldsymbol {P}}}
F
S
{\displaystyle {\boldsymbol {F}}{\boldsymbol {S}}}
R
T
{\displaystyle {\boldsymbol {R}}{\boldsymbol {T}}}
F
−
T
M
{\displaystyle {\boldsymbol {F}}^{-T}{\boldsymbol {M}}}
S
=
{\displaystyle {\boldsymbol {S}}=\,}
J
F
−
1
σ
F
−
T
{\displaystyle J{\boldsymbol {F}}^{-1}{\boldsymbol {\sigma }}{\boldsymbol {F}}^{-T}}
F
−
1
τ
F
−
T
{\displaystyle {\boldsymbol {F}}^{-1}{\boldsymbol {\tau }}{\boldsymbol {F}}^{-T}}
F
−
1
P
{\displaystyle {\boldsymbol {F}}^{-1}{\boldsymbol {P}}}
S
{\displaystyle {\boldsymbol {S}}}
U
−
1
T
{\displaystyle {\boldsymbol {U}}^{-1}{\boldsymbol {T}}}
C
−
1
M
{\displaystyle {\boldsymbol {C}}^{-1}{\boldsymbol {M}}}
T
=
{\displaystyle {\boldsymbol {T}}=\,}
J
R
T
σ
F
−
T
{\displaystyle J{\boldsymbol {R}}^{T}{\boldsymbol {\sigma }}{\boldsymbol {F}}^{-T}}
R
T
τ
F
−
T
{\displaystyle {\boldsymbol {R}}^{T}{\boldsymbol {\tau }}{\boldsymbol {F}}^{-T}}
R
T
P
{\displaystyle {\boldsymbol {R}}^{T}{\boldsymbol {P}}}
U
S
{\displaystyle {\boldsymbol {U}}{\boldsymbol {S}}}
T
{\displaystyle {\boldsymbol {T}}}
U
−
1
M
{\displaystyle {\boldsymbol {U}}^{-1}{\boldsymbol {M}}}
M
=
{\displaystyle {\boldsymbol {M}}=\,}
J
F
T
σ
F
−
T
{\displaystyle J{\boldsymbol {F}}^{T}{\boldsymbol {\sigma }}{\boldsymbol {F}}^{-T}}
F
T
τ
F
−
T
{\displaystyle {\boldsymbol {F}}^{T}{\boldsymbol {\tau }}{\boldsymbol {F}}^{-T}}
F
T
P
{\displaystyle {\boldsymbol {F}}^{T}{\boldsymbol {P}}}
C
S
{\displaystyle {\boldsymbol {C}}{\boldsymbol {S}}}
U
T
{\displaystyle {\boldsymbol {U}}{\boldsymbol {T}}}
M
{\displaystyle {\boldsymbol {M}}}
^ J. Bonet and R. W. Wood, Nonlinear Continuum Mechanics for Finite Element Analysis , Cambridge University Press.
^ R. W. Ogden, 1984, Non-linear Elastic Deformations , Dover.
^ L. D. Landau, E. M. Lifshitz, Theory of Elasticity , third edition
^ Three-Dimensional Elasticity ISBN 978-0-08-087541-5 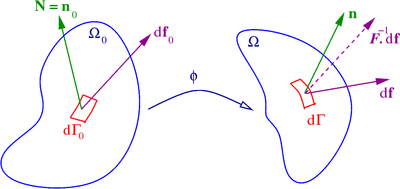





















































![{\displaystyle {\boldsymbol {S}}=\varphi ^{*}[{\boldsymbol {\tau }}]={\boldsymbol {F}}^{-1}\cdot {\boldsymbol {\tau }}\cdot {\boldsymbol {F}}^{-T}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a4d5f37efb8297f33270efe322adaabf46099ee9)
![{\displaystyle {\boldsymbol {\tau }}=\varphi _{*}[{\boldsymbol {S}}]={\boldsymbol {F}}\cdot {\boldsymbol {S}}\cdot {\boldsymbol {F}}^{T}~.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c3b707f11a8c67a3409dd4df7e6448d0ee9444cb)







































