Cramer's paradox

Cubic curves intersecting in 9 points

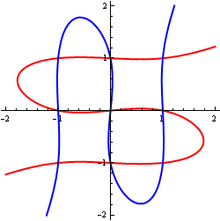
In mathematics, Cramer's paradox or the Cramer–Euler paradox is the statement that the number of points of intersection of two higher-order curves in the plane can be greater than the number of arbitrary points that are usually needed to define one such curve. It is named after the Genevan mathematician Gabriel Cramer.

This phenomenon appears paradoxical because the points of intersection fail to uniquely define any curve (they belong to at least two different curves) despite their large number. It is the result of a naive understanding or a misapplication of two theorems:

• Bézout's theorem states that the number of points of intersection of two algebraic curves is equal to the product of their degrees, provided that certain necessary conditions are met. In particular, two curves of degree $n$ generally have $n^{2}$ points of intersection.
• Cramer's theorem states that a curve of degree $n$ is determined by $n(n+3)/2$ points, again assuming that certain conditions hold.

For all $n\geq 3$, $n^{2}\geq n(n+3)/2$, so it would naively appear that for degree three or higher, the intersection of two curves would have enough points to define either of the curves uniquely. However, because these points belong to both curves, they do not define a unique curve of this degree. The resolution of the paradox is that the $n(n+3)/2$ bound on the number of points needed to define a curve only applies to points in general position. In certain degenerate cases, $n(n+3)/2$ points are not enough to determine a curve uniquely.

History

The paradox was first published by Colin Maclaurin. Cramer and Leonhard Euler corresponded on the paradox in letters of 1744 and 1745 and Euler explained the problem to Cramer. It has become known as Cramer's paradox after featuring in his 1750 book Introduction à l'analyse des lignes courbes algébriques, although Cramer quoted Maclaurin as the source of the statement. At about the same time, Euler published examples showing a cubic curve which was not uniquely defined by 9 points and discussed the problem in his book Introductio in analysin infinitorum. The result was publicized by James Stirling and explained by Julius Plücker.

No paradox for lines and nondegenerate conics

For first order curves (that is lines) the paradox does not occur, because $n=1$, so $n^{2}=1<n(n+3)/2=2$. In general two distinct lines intersect at a single point unless the lines are of equal slope, in which case they do not intersect at all. A single point is not sufficient to define a line (two are needed); through the point of intersection there pass not only the two given lines but an infinite number of other lines as well.

Two nondegenerate conics intersect in at most at four finite points in the real plane, which is precisely the number given as a maximum by Bézout's theorem. However, five points are needed to define a nondegenerate conic, so again in this case there is no paradox.

Cramer's example for cubic curves

In a letter to Euler, Cramer pointed out that the cubic curves $x^{3}-x=0$ and $y^{3}-y=0$ intersect in precisely nine points. The first equation defines three vertical lines $x=-1$, $x=0$, and $x=1$, and similarly the second equation defines three horizontal lines; these lines intersect in a grid of nine points. Hence nine points are not sufficient to uniquely determine a cubic curve in degenerate cases such as these.

Resolution

A bivariate equation of degree n has 1 + n(n + 3) / 2 coefficients, but the set of points described by the equation is preserved if the equation is divided through by one of the coefficients, leaving one coefficient equal to 1 and only n(n + 3) / 2 coefficients to characterize the curve. Given n(n + 3) / 2 points (x_i, y_i), each of these points can be used to create a separate equation by substituting it into the general polynomial equation of degree n, giving n(n + 3) / 2 equations linear in the n(n + 3) / 2 unknown coefficients. If this system is non-degenerate in the sense of having a non-zero determinant, the unknown coefficients are uniquely determined and hence the polynomial equation and its curve are uniquely determined. But if this determinant is zero, the system is degenerate and the points can be on more than one curve of degree n.

External links

• Ed Sandifer "Cramer’s Paradox"
• Cramer's Paradox at MathPages