Omnitruncated 5-simplex honeycomb
| Omnitruncated 5-simplex honeycomb | |
|---|---|
| (No image) | |
| Type | Uniform honeycomb |
| Family | Omnitruncated simplectic honeycomb |
| Schläfli symbol | t012345{3[6]} |
| Coxeter–Dynkin diagram | |
| 5-face types | t01234{3,3,3,3} |
| 4-face types | t0123{3,3,3} {}×t012{3,3} {6}×{6} |
| Cell types | t012{3,3} {4,3} {}x{6} |
| Face types | {4} {6} |
| Vertex figure | 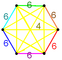 Irr. 5-simplex |
| Symmetry | ×12, [6[3[6]]] |
| Properties | vertex-transitive |
In five-dimensional Euclidean geometry, the omnitruncated 5-simplex honeycomb or omnitruncated hexateric honeycomb is a space-filling tessellation (or honeycomb). It is composed entirely of omnitruncated 5-simplex facets.
The facets of all omnitruncated simplectic honeycombs are called permutahedra and can be positioned in n+1 space with integral coordinates, permutations of the whole numbers (0,1,..,n).
A5* lattice
[edit]The A*
5 lattice (also called A6
5) is the union of six A5 lattices, and is the dual vertex arrangement to the omnitruncated 5-simplex honeycomb, and therefore the Voronoi cell of this lattice is an omnitruncated 5-simplex.
![]()
![]()
![]()
![]()
![]()
![]()
![]() ∪
∪
![]()
![]()
![]()
![]()
![]()
![]()
![]() ∪
∪
![]()
![]()
![]()
![]()
![]()
![]()
![]() ∪
∪
![]()
![]()
![]()
![]()
![]()
![]()
![]() ∪
∪
![]()
![]()
![]()
![]()
![]()
![]()
![]() ∪
∪
![]()
![]()
![]()
![]()
![]()
![]()
![]() = dual of
= dual of ![]()
![]()
![]()
![]()
![]()
![]()
![]()
Related polytopes and honeycombs
[edit]This honeycomb is one of 12 unique uniform honeycombs[1] constructed by the Coxeter group. The extended symmetry of the hexagonal diagram of the Coxeter group allows for automorphisms that map diagram nodes (mirrors) on to each other. So the various 12 honeycombs represent higher symmetries based on the ring arrangement symmetry in the diagrams:
| A5 honeycombs | ||||
|---|---|---|---|---|
| Hexagon symmetry |
Extended symmetry |
Extended diagram |
Extended group |
Honeycomb diagrams |
| a1 |
[3[6]] | |||
| d2 |
<[3[6]]> | ×21 | ||
| p2 |
[[3[6]]] | ×22 | ||
| i4 |
[<[3[6]]>] | ×21×22 | ||
| d6 |
<3[3[6]]> | ×61 | ||
| r12 |
[6[3[6]]] | ×12 | ||
Projection by folding
[edit]The omnitruncated 5-simplex honeycomb can be projected into the 3-dimensional omnitruncated cubic honeycomb by a geometric folding operation that maps two pairs of mirrors into each other, sharing the same 3-space vertex arrangement:
See also
[edit]Regular and uniform honeycombs in 5-space:
Notes
[edit]- ^ mathworld: Necklace, OEIS sequence A000029 13-1 cases, skipping one with zero marks
References
[edit]- Norman Johnson Uniform Polytopes, Manuscript (1991)
- Kaleidoscopes: Selected Writings of H. S. M. Coxeter, edited by F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss, Wiley-Interscience Publication, 1995, ISBN 978-0-471-01003-6 [1]
- (Paper 22) H.S.M. Coxeter, Regular and Semi Regular Polytopes I, [Math. Zeit. 46 (1940) 380-407, MR 2,10] (1.9 Uniform space-fillings)
- (Paper 24) H.S.M. Coxeter, Regular and Semi-Regular Polytopes III, [Math. Zeit. 200 (1988) 3-45]
| Space | Family | / / | ||||
|---|---|---|---|---|---|---|
| E2 | Uniform tiling | 0[3] | δ3 | hδ3 | qδ3 | Hexagonal |
| E3 | Uniform convex honeycomb | 0[4] | δ4 | hδ4 | qδ4 | |
| E4 | Uniform 4-honeycomb | 0[5] | δ5 | hδ5 | qδ5 | 24-cell honeycomb |
| E5 | Uniform 5-honeycomb | 0[6] | δ6 | hδ6 | qδ6 | |
| E6 | Uniform 6-honeycomb | 0[7] | δ7 | hδ7 | qδ7 | 222 |
| E7 | Uniform 7-honeycomb | 0[8] | δ8 | hδ8 | qδ8 | 133 • 331 |
| E8 | Uniform 8-honeycomb | 0[9] | δ9 | hδ9 | qδ9 | 152 • 251 • 521 |
| E9 | Uniform 9-honeycomb | 0[10] | δ10 | hδ10 | qδ10 | |
| E10 | Uniform 10-honeycomb | 0[11] | δ11 | hδ11 | qδ11 | |
| En-1 | Uniform (n-1)-honeycomb | 0[n] | δn | hδn | qδn | 1k2 • 2k1 • k21 |









