Folkman graph

Folkman graph
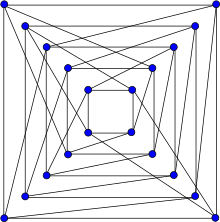The Folkman graph
Named after	Jon Folkman
Vertices	20
Edges	40
Radius	3
Diameter	4
Girth	4
Automorphisms	3840
Chromatic number	2
Chromatic index	4
Book thickness	3
Queue number	2
Properties	Hamiltonian Regular Bipartite Semi-symmetric Eulerian Perfect
Table of graphs and parameters

In the mathematical field of graph theory, the Folkman graph, named after Jon Folkman, is a bipartite 4-regular graph with 20 vertices and 40 edges.

The Folkman graph is Hamiltonian and has chromatic number 2, chromatic index 4, radius 3, diameter 4 and girth 4. It is also a 4-vertex-connected and 4-edge-connected perfect graph. It has book thickness 3 and queue number 2.

Algebraic properties

The automorphism group of the Folkman graph acts transitively on its edges but not on its vertices. It is the smallest undirected graph that is edge-transitive and regular, but not vertex-transitive. Such graphs are called semi-symmetric graphs and were first studied by Folkman in 1967 who discovered the graph on 20 vertices that now is named after him.

As a semi-symmetric graph, the Folkman graph is bipartite, and its automorphism group acts transitively on each of the two vertex sets of the bipartition. In the diagram below indicating the chromatic number of the graph, the green vertices can not be mapped to red ones by any automorphism, but any red vertex can be mapped on any other red vertex and any green vertex can be mapped on any other green vertex.

The characteristic polynomial of the Folkman graph is $(x-4)x^{10}(x+4)(x^{2}-6)^{4}$.

Gallery

• 
  The chromatic index of the Folkman graph is 4.
• 
  The chromatic number of the Folkman graph is 2.
• 
  The Folkman graph is Hamiltonian.