Archimedean graph
Appearance
In the mathematical field of graph theory, an Archimedean graph is a graph that forms the skeleton of one of the Archimedean solids. There are 13 Archimedean graphs, and all of them are regular, polyhedral (and therefore by necessity also 3-vertex-connected planar graphs), and also Hamiltonian graphs.[1]
Along with the 13, the set of infinite prism graphs and antiprism graphs can also be considered Archimedean graphs.[2]
| Name | Graph | Degree | Edges | Vertices | Order |
|---|---|---|---|---|---|
| truncated tetrahedral graph | 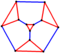 |
3 | 18 | 12 | 24 |
| cuboctahedral graph |  |
4 | 24 | 12 | 48 |
| truncated cubical graph |  |
3 | 36 | 24 | 48 |
| truncated octahedral graph |  |
3 | 36 | 24 | 48 |
| rhombicuboctahedral graph |  |
4 | 48 | 24 | 48 |
| truncated cuboctahedral graph (great rhombicuboctahedron) |
 |
3 | 72 | 48 | 48 |
| snub cubical graph |  |
5 | 60 | 24 | 24 |
| icosidodecahedral graph |  |
4 | 60 | 30 | 120 |
| truncated dodecahedral graph |  |
3 | 90 | 60 | 120 |
| truncated icosahedral graph | 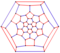 |
3 | 90 | 60 | 120 |
| rhombicosidodecahedral graph |  |
4 | 120 | 60 | 120 |
| truncated icosidodecahedral graph (great rhombicosidodecahedron) |
 |
3 | 180 | 120 | 120 |
| snub dodecahedral graph |  |
5 | 150 | 60 | 60 |
See also
References
- Read, R. C. and Wilson, R. J. An Atlas of Graphs, Oxford, England: Oxford University Press, 2004 reprint, Chapter 6 special graphs pp. 261, 267-269.
