Arithmetic billiards

In recreational mathematics, arithmetic billiards provide a geometrical method to determine the least common multiple and the greatest common divisor of two natural numbers by making use of reflections inside a rectangle whose sides are the two given numbers. This is an easy example of trajectory analysis of dynamical billiards.
Arithmetic billiards have been discussed as mathematical puzzles by Hugo Steinhaus[1] and Martin Gardner,[2] and are known to mathematics teachers under the name 'Paper Pool'.[3] They have been used as a source of questions in mathematical circles.[4]
The arithmetic billiard path
[edit]
Consider a rectangle with integer sides, and construct a path inside this rectangle as follows:
- start in a corner, and move along the straight line which makes a 45° angle with the sides;
- every time that the path hits a side, reflect it with the same angle (the path makes either a left or a right 90° turn);
- eventually (i.e. after a finite number of reflections) the path hits a corner and there it stops.
If one side length divides the other, the path is a zigzag consisting of one or more segments. Else, the path has self-intersections and consists of segments of various lengths in two orthogonal directions. In general, the path is the intersection of the rectangle with a grid of squares (oriented at 45° w.r.t. the rectangle sides).
Arithmetical features of the path
[edit]
Call and the side lengths of the rectangle, and divide this into unit squares. The least common multiple is the number of unit squares crossed by the arithmetic billiard path or, equivalently, the length of the path divided by . In particular, the path goes through each unit square if and only if and are coprime.
Suppose that none of the two side lengths divides the other. Then the first segment of the arithmetic billiard path contains the point of self-intersection which is closest to the starting point. The greatest common divisor is the number of unit squares crossed by the first segment of the path up to that point of self-intersection.
The number of bouncing points for the arithmetic billiard path on the two sides of length equals , and similarly for the two sides of length . In particular, if and are coprime, then the total number of contact points between the path and the perimeter of the rectangle (i.e. the bouncing points plus starting and ending corner) equals .
The ending corner of the path is opposite to the starting corner if and only if and are exactly divisible by the same power of two (for example, if they are both odd), else it is one of the two adjacent corners, according to whether or has more factors in its prime factorisation.
The path is symmetric: if the starting and the ending corner are opposite, then the path is pointsymmetric w.r.t. the center of the rectangle, else it is symmetric with respect to the bisector of the side connecting the starting and the ending corner.
The contact points between the arithmetic billiard path and the rectangle perimeter are evenly distributed: the distance along the perimeter (i.e. possibly going around the corner) between two such neighbouring points equals .
Set coordinates in the rectangle such that the starting point is and the opposite corner is . Then any point on the arithmetic billiard path which has integer coordinates has the property that the sum of the coordinates is even (the parity cannot change by moving along diagonals of unit squares). The points of self-intersection of the path, the bouncing points, and the starting and ending corner are exactly the points in the rectangle whose coordinates are multiples of and such that the sum of the coordinates is an even multiple of .
Ideas of proof
[edit]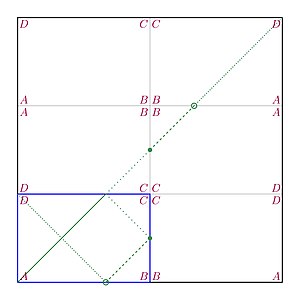
Reflecting the billiard: Consider a square with side . By displaying multiple copies of the original rectangle (with mirror symmetry) we can visualise the arithmetic billiard path as a diagonal of that square. In other words, we can think of reflecting the rectangle rather than the path segments.
Reducing to the coprime case: It is convenient to rescale the rectangle dividing and by their greatest common divisor, operation which does not alter the geometry of the path (e.g. the number of bouncing points).
Reversing the time: The motion of the path is “time reversible”, meaning that if the path is currently traversing one particular unit square (in a particular direction), then there is absolutely no doubt from which unit square and from which direction it just came.[4]
The proof can be found in a popularization article.[5]
One generalisation
[edit]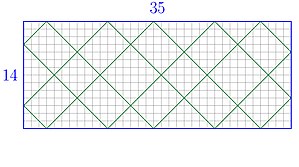
If we allow the starting point of the path to be any point in the rectangle with integer coordinates, then there are also periodic paths unless the rectangle sides are coprime. The length of any periodic path equals .
References
[edit]- ^ Steinhaus, Hugo (1999). Mathematical Snapshots (Dover Recreational Math Series ed.). Courier Corporation. p. 63. ISBN 0486409147.
- ^ Gardner, Martin (1984). Sixth Book of Mathematical Diversions from "Scientific American". University of Chicago Press. pp. 211–215. ISBN 0226282503.
- ^ "Paper Pool Game". NCTM Illuminations. National Council of Teachers of Mathematics. Retrieved 10 January 2018.
- ^ a b Tanton, James (2012). Mathematical Galore! The First Five Years of the St. Mark's Institute of Mathematics. The Mathematical Association of America. pp. 145–156. ISBN 978-0883857762.
- ^ Perucca, Antonella (April 24, 2018). "Arithmetic Billiards". Plus Magazine. University of Cambridge. Retrieved December 23, 2018.














