Bisection bandwidth

In computer networking, a network may be bisected into two equal-sized partitions. The bisection bandwidth of a network topology is the minimum bandwidth available between any two such partitions.^[1] Given a graph $G$ with vertices $V$ , edges $E$ , and edge weights $w$ , the bisection bandwidth of $G$ is

$BB(G)=\min _{S\subset V:|S|={\frac {1}{2}}|V|}\quad \sum _{u\in S,v\not \in S}w(u,v)$ .

In other words, the network is bisected s in such a way that the bandwidth between the two partitions is minimum.^[2] A network is considered to have full bisection bandwidth if $BB(G)\geq {\frac {1}{2}}|V|$ .^[3] Intuitively, full bisection bandwidth means that if all vertices in the network are matched as source-destination pairs, then if all pairs send flow at rate 1 simultaneously, there are no bisection bottlenecks. Therefore, bisection bandwidth accounts for the bottleneck bandwidth of the bisected network as a whole.

Bisection bandwidth calculations

For a linear array with n nodes bisection bandwidth is one link bandwidth. For linear array only one link needs to be broken to bisect the network into two partitions.

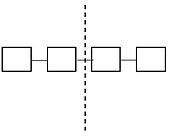
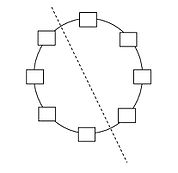
For ring topology with n nodes two links should be broken to bisect the network, so bisection bandwidth becomes bandwidth of two links.

For tree topology with n nodes can be bisected at the root by breaking one link, so bisection bandwidth is one link bandwidth.

For Mesh topology with n nodes, ${\sqrt {n}}$ links should be broken to bisect the network, so bisection bandwidth is bandwidth of ${\sqrt {n}}$ links.

For Hyper-cube topology with n nodes, n/2 links should be broken to bisect the network, so bisection bandwidth is bandwidth of n/2 links.

^[2]

Significance of bisection bandwidth

Theoretical support for the importance of this measure of network performance was developed in the PhD research of Clark Thomborson (formerly Clark Thompson).^[4] Thomborson proved that important algorithms for sorting, Fast Fourier transformation, and matrix-matrix multiplication become communication-limited—as opposed to CPU-limited or memory-limited—on computers with insufficient bisection bandwidth. F. Thomson Leighton's PhD research^[5] tightened Thomborson's loose bound ^[6] on the bisection bandwidth of a computationally-important variant of the De Bruijn graph known as the shuffle-exchange network. Based on Bill Dally's analysis of latency, average-case throughput, and hot-spot throughput of m-ary n-cube networks^[2] for various m, it can be observed that low-dimensional networks, in comparison to high-dimensional networks (e.g., binary n-cubes) with the same bisection bandwidth (e.g., tori), have reduced latency and higher hot-spot throughput.^[7]

Note, there is also support that bisection bandwidth and network throughput are asymptotically different metrics, which may grow at different rates depending on the network topology. ^[3]^[8]

References

^ John L. Hennessy and David A. Patterson (2003). Computer Architecture: A Quantitative Approach (Third ed.). Morgan Kaufmann Publishers, Inc. p. 789. ISBN 978-1-55860-596-1.
^ ^a ^b ^c Solihin, Yan (2016). Fundamentals of parallel multicore architecture. CRC Press. pp. 371–381. ISBN 9781482211191.
^ ^a ^b Namyar, Pooria; Supittayapornpong, Sucha; Zhang, Mingyang; Yu, Minlan; Govindan, Ramesh (2021-08-09). "A throughput-centric view of the performance of datacenter topologies". Proceedings of the 2021 ACM SIGCOMM 2021 Conference. SIGCOMM '21. New York, NY, USA: Association for Computing Machinery: 349–369. doi:10.1145/3452296.3472913. ISBN 978-1-4503-8383-7.
^ C. D. Thompson (1980). A complexity theory for VLSI (PDF) (Thesis). Carnegie-Mellon University.
^ F. Thomson Leighton (1983). Complexity Issues in VLSI: Optimal layouts for the shuffle-exchange graph and other networks (Thesis). MIT Press. ISBN 0-262-12104-2.
^ Clark Thompson (1979). Area-time complexity for VLSI. Proc. Caltech Conf. on VLSI Systems and Computations. pp. 81–88.
^ Bill Dally (1990). "Performance analysis of k-ary n-cube interconnection networks". IEEE Transactions on Computers. 39 (6): 775–785. CiteSeerX 10.1.1.473.5096. doi:10.1109/12.53599.
^ Jyothi, Sangeetha Abdu; Singla, Ankit; Godfrey, P. Brighten; Kolla, Alexandra (2014-06-16). "Measuring throughput of data center network topologies". The 2014 ACM international conference on Measurement and modeling of computer systems. SIGMETRICS '14. New York, NY, USA: Association for Computing Machinery: 597–598. doi:10.1145/2591971.2592040. ISBN 978-1-4503-2789-3.

This computer networking article is a stub. You can help Wikipedia by expanding it.

[1] John L. Hennessy and David A. Patterson (2003). Computer Architecture: A Quantitative Approach (Third ed.). Morgan Kaufmann Publishers, Inc. p. 789. ISBN 978-1-55860-596-1.

[:0-2] Solihin, Yan (2016). Fundamentals of parallel multicore architecture. CRC Press. pp. 371–381. ISBN 9781482211191.

[:1-3] Namyar, Pooria; Supittayapornpong, Sucha; Zhang, Mingyang; Yu, Minlan; Govindan, Ramesh (2021-08-09). "A throughput-centric view of the performance of datacenter topologies". Proceedings of the 2021 ACM SIGCOMM 2021 Conference. SIGCOMM '21. New York, NY, USA: Association for Computing Machinery: 349–369. doi:10.1145/3452296.3472913. ISBN 978-1-4503-8383-7.

[4] C. D. Thompson (1980). A complexity theory for VLSI (PDF) (Thesis). Carnegie-Mellon University.

[5] F. Thomson Leighton (1983). Complexity Issues in VLSI: Optimal layouts for the shuffle-exchange graph and other networks (Thesis). MIT Press. ISBN 0-262-12104-2.

[6] Clark Thompson (1979). Area-time complexity for VLSI. Proc. Caltech Conf. on VLSI Systems and Computations. pp. 81–88.

[7] Bill Dally (1990). "Performance analysis of k-ary n-cube interconnection networks". IEEE Transactions on Computers. 39 (6): 775–785. CiteSeerX 10.1.1.473.5096. doi:10.1109/12.53599.

[8] Jyothi, Sangeetha Abdu; Singla, Ankit; Godfrey, P. Brighten; Kolla, Alexandra (2014-06-16). "Measuring throughput of data center network topologies". The 2014 ACM international conference on Measurement and modeling of computer systems. SIGMETRICS '14. New York, NY, USA: Association for Computing Machinery: 597–598. doi:10.1145/2591971.2592040. ISBN 978-1-4503-2789-3.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]