Blinder–Oaxaca decomposition
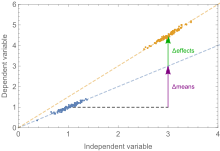
The Blinder–Oaxaca decomposition (/ˈblaɪndərwɑːˈhɑːkɑː/), also known as Kitagawa decomposition, is a statistical method that explains the difference in the means of a dependent variable between two groups by decomposing the gap into within-group and between-group differences in the effect of the explanatory variable.
The method was introduced by sociologist and demographer Evelyn M. Kitagawa in 1955.[1] Ronald Oaxaca introduced this method in economics in his doctoral thesis at Princeton University and eventually published in 1973.[2] The decomposition technique also carries the name of Alan Blinder who proposed a similar approach in the same year.[3] Oaxaca's original research question was the wage differential between two different groups of workers (male vs. female), but the method has since been applied to numerous other topics.[4]
Method[edit]
The following three equations illustrate this decomposition. Estimate separate linear wage regressions for individuals i in groups A and B:
where Χ is a vector of explanatory variables such as education, experience, industry, and occupation, βA and βB are vectors of coefficients and μ is an error term.
Let bA and bB be respectively the regression estimates of βA and βB. Then, since the average value of residuals in a linear regression is zero, we have:
The first part of the last line of (3) is the impact of between-group differences in the explanatory variables X, evaluated using the coefficients for group A. The second part is the differential not explained by these differences in observed characteristics X.
Interpretation[edit]
The unexplained differential in wages for the same values of explanatory variables should not be interpreted as the amount of the difference in wages due only to discrimination (against women in Oaxaca's application). This is because other explanatory variables not included in the regression (e.g. because they are unobserved) may also account for wage differences. For example, David Card and Alan Krueger found in a paper entitled, "School Quality and Black-White Relative Earnings: A Direct Assessment"[5] that improvements in the quality of schools for Black men born in the Southern states of the United States between 1915 and 1966 increased the return to education for these men, leading to narrowing of the black-white earnings gap. In terms of wage regressions, the poor quality of schools for Black men had meant a lower value of the β coefficient on years of schooling for Black men than for White men. Thus, some of this lower β coefficient reflected a difference in the quality of education for Black workers which could have otherwise been interpreted as an effect of direct discrimination; differences in the quality of education for Black workers would reflect historical or 'indirect' discrimination against them.
Differences between Kitagawa and Blinder–Oaxaca[edit]
Oaxaca and Sierminska argued that the Blinder–Oaxaca decomposition is a generalization of the Kitagawa decomposition.[6]
See also[edit]
References[edit]
- ^ Kitagawa, Evelyn M. (1955). "Components of a Difference Between Two Rates". Journal of the American Statistical Association. 50 (272): 1168–1194. doi:10.2307/2281213. JSTOR 2281213.
- ^ Oaxaca, R. (1973). "Male-Female Wage Differentials in Urban Labor Markets". International Economic Review. 14 (3): 693–709. doi:10.2307/2525981. JSTOR 2525981.
- ^ Blinder, A. S. (1973). "Wage Discrimination: Reduced Form and Structural Estimates". Journal of Human Resources. 8 (4): 436–455. doi:10.2307/144855. JSTOR 144855.
- ^ O'Donnell, Owen A.; et al. (2008). "Explaining Differences between Groups: Oaxaca Decomposition". Analyzing Health Equity Using Household Survey Data: A Guide to Techniques and Their Implementation. World Bank Publications. pp. 147–158. ISBN 9780821369340.
- ^ Card, David; Krueger, Alan (1992). "School Quality and Black-White Relative Earnings: A Direct Assessment" (PDF). Quarterly Journal of Economics. 107 (1): 151–200. doi:10.2307/2118326. JSTOR 2118326. S2CID 150859258.
- ^ Oaxaca; Sierminska (May 2023). "Oaxaca-Blinder Meets Kitagawa: What Is the Link?" (PDF). IZA Discussion Papers. IZA DP No. (16188).
Further reading[edit]
- Autor, David (January 30, 2015). "MIT Graduate Labor Economics 14.662 Spring 2015 Lecture Note 1: Wage Density Decompositions" (PDF). Massachusetts Institute of Technology: MIT OpenCourseWare.
- Borjas, George J. (2000). "Measuring Discrimination". Labor Economics (Second ed.). Boston: Irwin McGraw-Hill. pp. 362–366. ISBN 0-07-231198-3.
- Cahuc, Pierre; Carcillo, Stéphane; Zylberberg, André (2014). "Decomposition Methods: The Case of the Gender Wage Gap". Labor Economics. Cambridge: MIT Press. pp. 504–514. ISBN 978-0-262-02770-0.
- Fortin, Nicole; Lemieux, Thomas; Firpo, Sergio (2011). "Decomposition Methods in Economics". Handbook of Labor Economics (PDF). Elsevier. pp. 1–102. doi:10.1016/S0169-7218(11)00407-2. ISBN 978-0-444-53450-7.
- Kevin Guo & Guillaume Basse. 2021. "The Generalized Oaxaca-Blinder Estimator." Journal of the American Statistical Association.


![{\displaystyle {\begin{aligned}(3)\qquad &\operatorname {mean} (\ln({\text{wages}}_{A}))-\operatorname {mean} (\ln({\text{wages}}_{B}))\\[4pt]={}&b_{A}\operatorname {mean} (X_{A})-b_{B}\operatorname {mean} (X_{B})\\[4pt]={}&b_{A}(\operatorname {mean} (X_{A})-\operatorname {mean} (X_{B}))+\operatorname {mean} (X_{B})(b_{A}-b_{B})\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e50f13499df60059982b9094fbe754d31a22ec62)