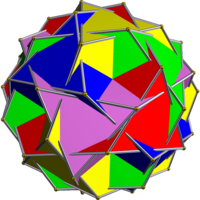
Compound of five truncated tetrahedra
Appearance
| Compound of five truncated tetrahedra | |
|---|---|
| |
| Type | Uniform compound |
| Index | UC55 |
| Polyhedra | 5 truncated tetrahedra |
| Faces | 20 triangles, 20 hexagons |
| Edges | 90 |
| Vertices | 60 |
| Dual | Compound of five triakis tetrahedra |
| Symmetry group | chiral icosahedral (I) |
| Subgroup restricting to one constituent | chiral tetrahedral (T) |

The compound of five truncated tetrahedra is a uniform polyhedron compound. It's composed of 5 truncated tetrahedra rotated around a common axis. It may be formed by truncating each of the tetrahedra in the compound of five tetrahedra. A far-enough truncation creates the compound of five octahedra. Its convex hull is a nonuniform snub dodecahedron.
Cartesian coordinates
[edit]Cartesian coordinates for the vertices of this compound are all the cyclic permutations of
- (±1, ±1, ±3)
- (±τ−1, ±(−τ−2), ±2τ)
- (±τ, ±(−2τ−1), ±τ2)
- (±τ2, ±(−τ−2), ±2)
- (±(2τ−1), ±1, ±(2τ − 1))
with an even number of minuses in the choices for '±', where τ = (1+√5)/2 is the golden ratio (sometimes written φ).
References
[edit]- Skilling, John (1976), "Uniform Compounds of Uniform Polyhedra", Mathematical Proceedings of the Cambridge Philosophical Society, 79: 447–457, doi:10.1017/S0305004100052440, MR 0397554.
