Iterative deepening depth-first search
This article needs additional citations for verification. (January 2017) |
| Class | Search algorithm |
|---|---|
| Data structure | Tree, Graph |
| Worst-case performance | , where is the branching factor and is the depth of the shallowest solution |
| Worst-case space complexity | [1]: 5 |
| Optimal | yes (for unweighted graphs) |
In computer science, iterative deepening search or more specifically iterative deepening depth-first search[2] (IDS or IDDFS) is a state space/graph search strategy in which a depth-limited version of depth-first search is run repeatedly with increasing depth limits until the goal is found. IDDFS is optimal, meaning that it finds the shallowest goal.[3] Since it visits all the nodes in the search tree down to depth before visiting any nodes at depth , the cumulative order in which nodes are first visited is effectively the same as in breadth-first search. However, IDDFS uses much less memory.[1]
Algorithm for directed graphs[edit]
The following pseudocode shows IDDFS implemented in terms of a recursive depth-limited DFS (called DLS) for directed graphs. This implementation of IDDFS does not account for already-visited nodes.
function IDDFS(root) is
for depth from 0 to ∞ do
found, remaining ← DLS(root, depth)
if found ≠ null then
return found
else if not remaining then
return null
function DLS(node, depth) is
if depth = 0 then
if node is a goal then
return (node, true)
else
return (null, true) (Not found, but may have children)
else if depth > 0 then
any_remaining ← false
foreach child of node do
found, remaining ← DLS(child, depth−1)
if found ≠ null then
return (found, true)
if remaining then
any_remaining ← true (At least one node found at depth, let IDDFS deepen)
return (null, any_remaining)
If the goal node is found by DLS, IDDFS will return it without looking deeper. Otherwise, if at least one node exists at that level of depth, the remaining flag will let IDDFS continue.
2-tuples are useful as return value to signal IDDFS to continue deepening or stop, in case tree depth and goal membership are unknown a priori. Another solution could use sentinel values instead to represent not found or remaining level results.
Properties[edit]
IDDFS achieves breadth-first search's completeness (when the branching factor is finite) using depth-first search's space-efficiency. If a solution exists, it will find a solution path with the fewest arcs.[3]
Iterative deepening visits states multiple times, and it may seem wasteful. However, if IDDFS explores a search tree to depth , most of the total effort is in exploring the states at depth . Relative to the number of states at depth , the cost of repeatedly visiting the states above this depth is always small.[4]
The main advantage of IDDFS in game tree searching is that the earlier searches tend to improve the commonly used heuristics, such as the killer heuristic and alpha–beta pruning, so that a more accurate estimate of the score of various nodes at the final depth search can occur, and the search completes more quickly since it is done in a better order. For example, alpha–beta pruning is most efficient if it searches the best moves first.[4]
A second advantage is the responsiveness of the algorithm. Because early iterations use small values for , they execute extremely quickly. This allows the algorithm to supply early indications of the result almost immediately, followed by refinements as increases. When used in an interactive setting, such as in a chess-playing program, this facility allows the program to play at any time with the current best move found in the search it has completed so far. This can be phrased as each depth of the search corecursively producing a better approximation of the solution, though the work done at each step is recursive. This is not possible with a traditional depth-first search, which does not produce intermediate results.
Asymptotic analysis[edit]
Time complexity[edit]
The time complexity of IDDFS in a (well-balanced) tree works out to be the same as breadth-first search, i.e. ,[1]: 5 where is the branching factor and is the depth of the goal.
Proof[edit]
In an iterative deepening search, the nodes at depth are expanded once, those at depth are expanded twice, and so on up to the root of the search tree, which is expanded times.[1]: 5 So the total number of expansions in an iterative deepening search is
where is the number of expansions at depth , is the number of expansions at depth , and so on. Factoring out gives
Now let . Then we have
This is less than the infinite series
which converges to
- , for
That is, we have
, for
Since or is a constant independent of (the depth), if (i.e., if the branching factor is greater than 1), the running time of the depth-first iterative deepening search is .
Example[edit]
For and the number is
All together, an iterative deepening search from depth all the way down to depth expands only about more nodes than a single breadth-first or depth-limited search to depth , when .[5]
The higher the branching factor, the lower the overhead of repeatedly expanded states,[1]: 6 but even when the branching factor is 2, iterative deepening search only takes about twice as long as a complete breadth-first search. This means that the time complexity of iterative deepening is still .
Space complexity[edit]
The space complexity of IDDFS is ,[1]: 5 where is the depth of the goal.
Proof[edit]
Since IDDFS, at any point, is engaged in a depth-first search, it need only store a stack of nodes which represents the branch of the tree it is expanding. Since it finds a solution of optimal length, the maximum depth of this stack is , and hence the maximum amount of space is .
In general, iterative deepening is the preferred search method when there is a large search space and the depth of the solution is not known.[4]
Example[edit]
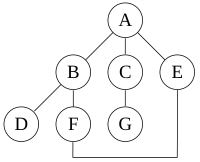
For the following graph:
a depth-first search starting at A, assuming that the left edges in the shown graph are chosen before right edges, and assuming the search remembers previously-visited nodes and will not repeat them (since this is a small graph), will visit the nodes in the following order: A, B, D, F, E, C, G. The edges traversed in this search form a Trémaux tree, a structure with important applications in graph theory.
Performing the same search without remembering previously visited nodes results in visiting nodes in the order A, B, D, F, E, A, B, D, F, E, etc. forever, caught in the A, B, D, F, E cycle and never reaching C or G.
Iterative deepening prevents this loop and will reach the following nodes on the following depths, assuming it proceeds left-to-right as above:
- 0: A
- 1: A, B, C, E
(Iterative deepening has now seen C, when a conventional depth-first search did not.)
- 2: A, B, D, F, C, G, E, F
(It still sees C, but that it came later. Also it sees E via a different path, and loops back to F twice.)
- 3: A, B, D, F, E, C, G, E, F, B
For this graph, as more depth is added, the two cycles "ABFE" and "AEFB" will simply get longer before the algorithm gives up and tries another branch.
Related algorithms[edit]
Similar to iterative deepening is a search strategy called iterative lengthening search that works with increasing path-cost limits instead of depth-limits. It expands nodes in the order of increasing path cost; therefore the first goal it encounters is the one with the cheapest path cost. But iterative lengthening incurs substantial overhead that makes it less useful than iterative deepening.[4]
Iterative deepening A* is a best-first search that performs iterative deepening based on "f"-values similar to the ones computed in the A* algorithm.
Bidirectional IDDFS[edit]
IDDFS has a bidirectional counterpart,[1]: 6 which alternates two searches: one starting from the source node and moving along the directed arcs, and another one starting from the target node and proceeding along the directed arcs in opposite direction (from the arc's head node to the arc's tail node). The search process first checks that the source node and the target node are same, and if so, returns the trivial path consisting of a single source/target node. Otherwise, the forward search process expands the child nodes of the source node (set ), the backward search process expands the parent nodes of the target node (set ), and it is checked whether and intersect. If so, a shortest path is found. Otherwise, the search depth is incremented and the same computation takes place.
One limitation of the algorithm is that the shortest path consisting of an odd number of arcs will not be detected. Suppose we have a shortest path When the depth will reach two hops along the arcs, the forward search will proceed from to , and the backward search will proceed from to . Pictorially, the search frontiers will go through each other, and instead a suboptimal path consisting of an even number of arcs will be returned. This is illustrated in the below diagrams:

What comes to space complexity, the algorithm colors the deepest nodes in the forward search process in order to detect existence of the middle node where the two search processes meet.
Additional difficulty of applying bidirectional IDDFS is that if the source and the target nodes are in different strongly connected components, say, , if there is no arc leaving and entering , the search will never terminate.
Time and space complexities[edit]
The running time of bidirectional IDDFS is given by
and the space complexity is given by
where is the number of nodes in the shortest -path. Since the running time complexity of iterative deepening depth-first search is , the speedup is roughly
Pseudocode[edit]
function Build-Path(s, μ, B) is
π ← Find-Shortest-Path(s, μ) (Recursively compute the path to the relay node)
remove the last node from π
return π B (Append the backward search stack)
function Depth-Limited-Search-Forward(u, Δ, F) is
if Δ = 0 then
F ← F {u} (Mark the node)
return
foreach child of u do
Depth-Limited-Search-Forward(child, Δ − 1, F)
function Depth-Limited-Search-Backward(u, Δ, B, F) is
prepend u to B
if Δ = 0 then
if u in F then
return u (Reached the marked node, use it as a relay node)
remove the head node of B
return null
foreach parent of u do
μ ← Depth-Limited-Search-Backward(parent, Δ − 1, B, F)
if μ null then
return μ
remove the head node of B
return null
function Find-Shortest-Path(s, t) is
if s = t then
return <s>
F, B, Δ ← ∅, ∅, 0
forever do
Depth-Limited-Search-Forward(s, Δ, F)
foreach δ = Δ, Δ + 1 do
μ ← Depth-Limited-Search-Backward(t, δ, B, F)
if μ null then
return Build-Path(s, μ, B) (Found a relay node)
F, Δ ← ∅, Δ + 1
References[edit]
- ^ a b c d e f g KORF, Richard E. (1985). "Depth-first iterative deepening" (PDF).
{{cite journal}}: Cite journal requires|journal=(help) - ^ Korf, Richard (1985). "Depth-first Iterative-Deepening: An Optimal Admissible Tree Search". Artificial Intelligence. 27: 97–109. doi:10.1016/0004-3702(85)90084-0. S2CID 10956233.
- ^ a b David Poole; Alan Mackworth. "3.5.3 Iterative Deepening‣ Chapter 3 Searching for Solutions ‣ Artificial Intelligence: Foundations of Computational Agents, 2nd Edition". artint.info. Retrieved 29 November 2018.
- ^ a b c d Russell, Stuart J.; Norvig, Peter (2003), Artificial Intelligence: A Modern Approach (2nd ed.), Upper Saddle River, New Jersey: Prentice Hall, ISBN 0-13-790395-2
- ^ Russell; Norvig (1994). Artificial Intelligence: A Modern Approach.