Descendant tree (group theory)
In mathematics, specifically group theory, a descendant tree is a hierarchical structure that visualizes parent-descendant relations between isomorphism classes of finite groups of prime power order , for a fixed prime number and varying integer exponents . Such groups are briefly called finite p-groups. The vertices of a descendant tree are isomorphism classes of finite p-groups.
Additionally to their order , finite p-groups have two further related invariants, the nilpotency class and the coclass . It turned out that descendant trees of a particular kind, the so-called pruned coclass trees whose infinitely many vertices share a common coclass , reveal a repeating finite pattern. These two crucial properties of finiteness and periodicity admit a characterization of all members of the tree by finitely many parametrized presentations. Consequently, descendant trees play a fundamental role in the classification of finite p-groups. By means of kernels and targets of Artin transfer homomorphisms, descendant trees can be endowed with additional structure.
An important question is how the descendant tree can actually be constructed for an assigned starting group which is taken as the root of the tree. The p-group generation algorithm is a recursive process for constructing the descendant tree of a given finite p-group playing the role of the tree root. This algorithm is implemented in the computational algebra systems GAP and Magma.
Definitions and terminology
[edit]According to M. F. Newman,[1] there exist several distinct definitions of the parent of a finite p-group . The common principle is to form the quotient of by a suitable normal subgroup which can be either
- the centre of , whence is called the central quotient of , or
- the last non-trivial term of the lower central series of , where denotes the nilpotency class of , or
- the last non-trivial term of the lower exponent-p central series of , where denotes the exponent-p class of , or
- the last non-trivial term of the derived series of , where denotes the derived length of .
In each case, is called an immediate descendant of and a directed edge of the tree is defined either by in the direction of the canonical projection onto the quotient or by in the opposite direction, which is more usual for descendant trees. The former convention is adopted by C. R. Leedham-Green and M. F. Newman,[2] by M. du Sautoy and D. Segal,[3] by C. R. Leedham-Green and S. McKay,[4] and by B. Eick, C. R. Leedham-Green, M. F. Newman and E. A. O'Brien.[5] The latter definition is used by M. F. Newman,[1] by M. F. Newman and E. A. O'Brien,[6] by M. du Sautoy,[7] and by B. Eick and C. R. Leedham-Green.[8]
In the following, the direction of the canonical projections is selected for all edges. Then, more generally, a vertex is a descendant of a vertex , and is an ancestor of , if either is equal to or there is a path
- , with ,
of directed edges from to . The vertices forming the path necessarily coincide with the iterated parents of , with :
- , with ,
In the most important special case (P2) of parents defined as last non-trivial lower central quotients, they can also be viewed as the successive quotients of class of when the nilpotency class of is given by :
- , with .
Generally, the descendant tree of a vertex is the subtree of all descendants of , starting at the root . The maximal possible descendant tree of the trivial group contains all finite p-groups and is somewhat exceptional, since, for any parent definition (P1–P4), the trivial group has infinitely many abelian p-groups as its immediate descendants. The parent definitions (P2–P3) have the advantage that any non-trivial finite p-group (of order divisible by ) possesses only finitely many immediate descendants.
Pro-p groups and coclass trees
[edit]For a sound understanding of coclass trees as a particular instance of descendant trees, it is necessary to summarize some facts concerning infinite topological pro-p groups. The members , with , of the lower central series of a pro-p group are closed (and open) subgroups of finite index, and therefore the corresponding quotients are finite p-groups. The pro-p group is said to be of coclass when the limit of the coclass of the successive quotients exists and is finite. An infinite pro-p group of coclass is a p-adic pre-space group ,[5] since it has a normal subgroup , the translation group, which is a free module over the ring of p-adic integers of uniquely determined rank , the dimension, such that the quotient is a finite p-group, the point group, which acts on uniserially. The dimension is given by
, with some .
A central finiteness result for infinite pro-p groups of coclass is provided by the so-called Theorem D, which is one of the five Coclass Theorems proved in 1994 independently by A. Shalev [9] and by C. R. Leedham-Green ,[10] and conjectured in 1980 already by C. R. Leedham-Green and M. F. Newman.[2] Theorem D asserts that there are only finitely many isomorphism classes of infinite pro-p groups of coclass , for any fixed prime and any fixed non-negative integer . As a consequence, if is an infinite pro-p group of coclass , then there exists a minimal integer such that the following three conditions are satisfied for any integer .
- ,
- is not a lower central quotient of any infinite pro-p group of coclass which is not isomorphic to ,
- is cyclic of order .
The descendant tree , with respect to the parent definition (P2), of the root with minimal is called the coclass tree of and its unique maximal infinite (reverse-directed) path
is called the mainline (or trunk) of the tree.

Tree diagram
[edit]Further terminology, used in diagrams visualizing finite parts of descendant trees, is explained in Figure 1 by means of an artificial abstract tree. On the left hand side, a level indicates the basic top-down design of a descendant tree. For concrete trees, such as those in Figure 2, resp. Figure 3, etc., the level is usually replaced by a scale of orders increasing from the top to the bottom. A vertex is capable (or extendable) if it has at least one immediate descendant, otherwise it is terminal (or a leaf). Vertices sharing a common parent are called siblings.
If the descendant tree is a coclass tree with root and with mainline vertices labelled according to the level , then the finite subtree defined as the difference set
is called the nth branch (or twig) of the tree or also the branch with root , for any . The depth of a branch is the maximal length of the paths connecting its vertices with its root. Figure 1 shows an artificial abstract coclass tree whose branches and both have depth , and the branches and are pairwise isomorphic as graphs. If all vertices of depth bigger than a given integer are removed from the branch , then we obtain the depth- pruned branch . Correspondingly, the depth- pruned coclass tree , resp. the entire coclass tree , consists of the infinite sequence of its pruned branches , resp. branches , connected by the mainline, whose vertices are called infinitely capable.
Virtual periodicity
[edit]The periodicity of branches of depth-pruned coclass trees has been proved with analytic methods using zeta functions [3] of groups by M. du Sautoy ,[7] and with algebraic techniques using cohomology groups by B. Eick and C. R. Leedham-Green .[8] The former methods admit the qualitative insight of ultimate virtual periodicity, the latter techniques determine the quantitative structure.
Theorem. For any infinite pro-p group of coclass and dimension , and for any given depth , there exists an effective minimal lower bound , where periodicity of length of pruned branches of the coclass tree sets in, that is, there exist graph isomorphisms
for all .
For the proof, click show on the right hand side.
The graph isomorphisms of depth- pruned branches with roots of sufficiently large order are derived with cohomological methods in Theorem 6, p. 277 and Theorem 9, p. 278 by Eick and Leedham-Green [8] and the effective lower bound for the branch root orders is established in Theorem 29, p. 287, of this article.
These central results can be expressed ostensively: When we look at a coclass tree through a pair of blinkers and ignore a finite number of pre-periodic branches at the top, then we shall see a repeating finite pattern (ultimate periodicity). However, if we take wider blinkers the pre-periodic initial section may become longer (virtual periodicity).
The vertex is called the periodic root of the pruned coclass tree, for a fixed value of the depth . See Figure 1.
Multifurcation and coclass graphs
[edit]Assume that parents of finite p-groups are defined as last non-trivial lower central quotients (P2). For a p-group of coclass , we can distinguish its (entire) descendant tree and its coclass- descendant tree , that is the subtree consisting of descendants of coclass only. The group is called coclass-settled if , i.e., if there are no descendants of with bigger coclass than .
The nuclear rank of in the theory of the p-group generation algorithm by M. F. Newman [11] and E. A. O'Brien [12] provides the following criteria.
- is terminal, and thus trivially coclass-settled, if and only if .
- If , then is capable, but it remains unknown whether is coclass-settled.
- If , then is capable and definitely not coclass-settled.
In the last case, a more precise assertion is possible: If has coclass and nuclear rank , then it gives rise to an m-fold multifurcation into a regular coclass-r descendant tree and irregular descendant graphs of coclass , for . Consequently, the descendant tree of is the disjoint union
.
Multifurcation is correlated with different orders of the last non-trivial lower central of immediate descendants. Since the nilpotency class increases exactly by a unit, , from a parent to any immediate descendant , the coclass remains stable, , if the last non-trivial lower central is cyclic of order , since then the exponent of the order also increases exactly by a unit, . In this case, is a regular immediate descendant with directed edge of step size , as usual. However, the coclass increases by , if with . Then is called an irregular immediate descendant with directed edge of step size .
If the condition of step size is imposed on all directed edges, then the maximal descendant tree of the trivial group splits into a countably infinite disjoint union
of directed coclass graphs , which are rather forests than trees. More precisely, the above-mentioned Coclass Theorems imply that
is the disjoint union of finitely many coclass trees of pairwise non-isomorphic infinite pro-p groups of coclass (Theorem D) and a finite subgraph of sporadic groups lying outside of any coclass tree.
Identifiers
[edit]The SmallGroups Library identifiers of finite groups, in particular of finite p-groups, given in the form
in the following concrete examples of descendant trees, are due to H. U. Besche, B. Eick and E. A. O'Brien .[13] [14] When the group orders are given in a scale on the left hand side, as in Figure 2 and Figure 3, the identifiers are briefly denoted by
.
Depending on the prime , there is an upper bound on the order of groups for which a SmallGroup identifier exists, e.g. for , and for . For groups of bigger orders, a notation with generalized identifiers resembling the descendant structure is employed. A regular immediate descendant, connected by an edge of step size with its parent , is denoted by
,
and an irregular immediate descendant, connected by an edge of step size with its parent , is denoted by
.
The implementations of the p-group generation algorithm in the computational algebra systems GAP and Magma use these generalized identifiers, which go back to J. A. Ascione in 1979 .[15]
Concrete examples of trees
[edit]In all examples, the underlying parent definition (P2) corresponds to the usual lower central series. Occasional differences to the parent definition (P3) with respect to the lower exponent-p central series are pointed out.
Coclass 0
[edit]The coclass graph
of finite p-groups of coclass does not contain any coclass tree and thus exclusively consists of sporadic groups, namely the trivial group and the cyclic group of order , which is a leaf (however, it is capable with respect to the lower exponent-p central series). For the SmallGroup identifier of is , for it is .

Coclass 1
[edit]The coclass graph
of finite p-groups of coclass , also called of maximal class, consists of the unique coclass tree with root , the elementary abelian p-group of rank , and a single isolated vertex (a terminal orphan without proper parent in the same coclass graph, since the directed edge to the trivial group has step size ), the cyclic group of order in the sporadic part (however, this group is capable with respect to the lower exponent-p central series). The tree is the coclass tree of the unique infinite pro-p group of coclass .
For , resp. , the SmallGroup identifier of the root is , resp. , and a tree diagram of the coclass graph from branch down to branch (counted with respect to the p-logarithm of the order of the branch root) is drawn in Figure 2, resp. Figure 3, where all groups of order at least are metabelian, that is non-abelian with derived length (vertices represented by black discs in contrast to contour squares indicating abelian groups). In Figure 3, smaller black discs denote metabelian 3-groups where even the maximal subgroups are non-abelian, a feature which does not occur for the metabelian 2-groups in Figure 2, since they all possess an abelian subgroup of index (usually exactly one). The coclass tree of , resp. , has periodic root and periodicity of length starting with branch , resp. periodic root and periodicity of length setting in with branch . Both trees have branches of bounded depth , so their virtual periodicity is in fact a strict periodicity.
However, the coclass tree of with has unbounded depth and contains non-metabelian groups, and the coclass tree of with has even unbounded width, that is, the number of descendants of a fixed order increases indefinitely with growing order .[16]
With the aid of kernels and targets of Artin transfers, the diagrams in Figure 2 and Figure 3 can be endowed with additional information and redrawn as structured descendant trees.
The concrete examples and of coclass graphs provide an opportunity to give a parametrized polycyclic power-commutator presentation [17] for the complete coclass tree , , mentioned in the lead section as a benefit of the descendant tree concept and as a consequence of the periodicity of the entire coclass tree. In both cases, a group is generated by two elements but the presentation contains the series of higher commutators , , starting with the main commutator . The nilpotency is formally expressed by the relation , when the group is of order .

For , there are two parameters and the pc-presentation is given by
The 2-groups of maximal class, that is of coclass , form three periodic infinite sequences,
- the dihedral groups, , , forming the mainline (with infinitely capable vertices),
- the generalized quaternion groups, , , which are all terminal vertices,
- the semidihedral groups, , , which are also leaves.
For , there are three parameters and and the pc-presentation is given by
3-groups with parameter possess an abelian maximal subgroup, those with parameter do not. More precisely, an existing abelian maximal subgroup is unique, except for the two extra special groups and , where all four maximal subgroups are abelian.
In contrast to any bigger coclass , the coclass graph exclusively contains p-groups with abelianization of type , except for its unique isolated vertex . The case is distinguished by the truth of the reverse statement: Any 2-group with abelianization of type is of coclass (O. Taussky's Theorem [18]).

Coclass 2
[edit]The genesis of the coclass graph with is not uniform. p-groups with several distinct abelianizations contribute to its constitution. For coclass , there are essential contributions from groups with abelianizations of the types , , , and an isolated contribution by the cyclic group of order :
.
Abelianization of type (p,p)
[edit]As opposed to p-groups of coclass with abelianization of type or , which arise as regular descendants of abelian p-groups of the same types, p-groups of coclass with abelianization of type arise from irregular descendants of a non-abelian p-group of coclass which is not coclass-settled.
For the prime , such groups do not exist at all, since the 2-group is coclass settled, which is the deeper reason for Taussky's Theorem. This remarkable fact has been observed by Giuseppe Bagnera [19] in 1898 already.
For odd primes , the existence of p-groups of coclass with abelianization of type is due to the fact that the group is not coclass-settled. Its nuclear rank equals , which gives rise to a bifurcation of the descendant tree into two coclass graphs. The regular component is a subtree of the unique tree in the coclass graph . The irregular component becomes a subgraph of the coclass graph when the connecting edges of step size of the irregular immediate descendants of are removed.
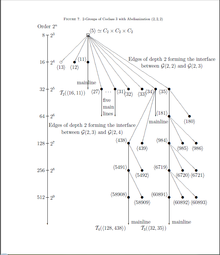
For , this subgraph is drawn in Figure 4, which shows the interface between finite 3-groups with coclass and of type . has seven top level vertices of three important kinds, all having order , which have been discovered by G. Bagnera .[19]
- Firstly, there are two terminal Schur σ-groups and in the sporadic part of the coclass graph .
- Secondly, the two groups and are roots of finite trees in the sporadic part . However, since they are not coclass-settled, the complete trees are infinite .
- Finally, the three groups , and give rise to (infinite) coclass trees, e.g., , , , each having a metabelian mainline, in the coclass graph . None of these three groups is coclass-settled.
Displaying additional information on kernels and targets of Artin transfers, we can draw these trees as structured descendant trees.
Definition. Generally, a Schur group (called a closed group by I. Schur, who coined the concept) is a pro-p group whose relation rank coincides with its generator rank . A σ-group is a pro-p group which possesses an automorphism inducing the inversion on its abelianization . A Schur σ-group is a Schur group which is also a σ-group and has a finite abelianization .
is not root of a coclass tree,
since its immediate descendant , which is root of a coclass tree with metabelian mainline vertices, has two siblings , resp. , which give rise to a single, resp. three, coclass tree(s) with non-metabelian mainline vertices having cyclic centres of order and branches of considerable complexity but nevertheless of bounded depth .
| Parameters |
Abelianization |
Class-2 quotient |
Class-3 quotient |
Class-4 quotient |
|---|---|---|---|---|
Pro-3 groups of coclass 2 with non-trivial centre
[edit]B. Eick, C. R. Leedham-Green, M. F. Newman and E. A. O'Brien [5] have constructed a family of infinite pro-3 groups with coclass having a non-trivial centre of order . The family members are characterized by three parameters . Their finite quotients generate all mainline vertices with bicyclic centres of type of six coclass trees in the coclass graph . The association of parameters to the roots of these six trees is given in Table 1, the tree diagrams, except for the abelianization , are indicated in Figure 4 and Figure 5, and the parametrized pro-3 presentation is given by

Abelianization of type (p²,p)
[edit]For , the top levels of the subtree of the coclass graph are drawn in Figure 5. The most important vertices of this tree are the eight siblings sharing the common parent , which are of three important kinds.
- Firstly, there are three leaves , , having cyclic centre of order , and a single leaf with bicyclic centre of type .
- Secondly, the group is root of a finite tree .
- Finally, the three groups , and give rise to infinite coclass trees, e.g., , , , each having a metabelian mainline, the first with cyclic centres of order , the second and third with bicyclic centres of type .
Here, is not root of a coclass tree, since aside from its descendant , which is root of a coclass tree with metabelian mainline vertices, it possesses five further descendants which give rise to coclass trees with non-metabelian mainline vertices having cyclic centres of order and branches of extreme complexity, here partially even with unbounded depth.[5]
Abelianization of type (p,p,p)
[edit]For , resp. , there exists a unique coclass tree with p-groups of type in the coclass graph . Its root is the elementary abelian p-group of type , that is, , resp. . This unique tree corresponds to the pro-2 group of the family by M. F. Newman and E. A. O'Brien,[6] resp. to the pro-3 group given by the parameters in Table 1. For , the tree is indicated in Figure 6, which shows some finite 2-groups with coclass of type .
Coclass 3
[edit]Here again, p-groups with several distinct abelianizations contribute to the constitution of the coclass graph . There are regular, resp. irregular, essential contributions from groups with abelianizations of the types , , , , resp. , , , and an isolated contribution by the cyclic group of order .
Abelianization of type (p,p,p)
[edit]Since the elementary abelian p-group of rank , that is, , resp. , for , resp. , is not coclass-settled, it gives rise to a multifurcation. The regular component has been described in the section about coclass . The irregular component becomes a subgraph of the coclass graph when the connecting edges of step size of the irregular immediate descendants of are removed.
For , this subgraph is contained in Figure 6. It has nine top level vertices of order which can be divided into terminal and capable vertices.
- The two groups and are leaves.
- The five groups and the two groups are infinitely capable.
The trees arising from the capable vertices are associated with infinite pro-2 groups by M. F. Newman and E. A. O'Brien [6] in the following manner.
gives rise to two trees,
associated with family , and
associated with family .
is associated with family .
is associated with family .
is associated with family .
gives rise to
associated with family . Finally,
is associated with family .
| SmallGroups identifier of Q |
Hall Senior classification of Q |
Schur multiplier |
2-rank of G' |
4-rank of G' |
Maximum of |
|---|---|---|---|---|---|
| 32.040 | |||||
| 32.041 | |||||
| 32.037 | |||||
| 32.038 | |||||
| 32.035 | |||||
| 32.036 | |||||
| 32.033 | or |
Hall-Senior classification of 2-groups
[edit]Seven of these nine top level vertices have been investigated by E. Benjamin, F. Lemmermeyer and C. Snyder [20] with respect to their occurrence as class-2 quotients of bigger metabelian 2-groups of type and with coclass , which are exactly the members of the descendant trees of the seven vertices. These authors use the classification of 2-groups by M. Hall and J. K. Senior [21] which is put in correspondence with the SmallGroups Library [13] in Table 2. The complexity of the descendant trees of these seven vertices increases with the 2-ranks and 4-ranks indicated in Table 2, where the maximal subgroups of index in are denoted by , for .
History
[edit]Descendant trees with central quotients as parents (P1) are implicit in P. Hall's 1940 paper [22] about isoclinism of groups. Trees with last non-trivial lower central quotients as parents (P2) were first presented by C. R. Leedham-Green at the International Congress of Mathematicians in Vancouver, 1974 .[1] The first extensive tree diagrams have been drawn manually by J. A. Ascione, G. Havas and C. R. Leedham-Green (1977) ,[23] by J. A. Ascione (1979) ,[15] and by B. Nebelung (1989) .[24] In the former two cases, the parent definition by means of the lower exponent-p central series (P3) was adopted in view of computational advantages, in the latter case, where theoretical aspects were focussed, the parents were taken with respect to the usual lower central series (P2).
See also
[edit]- The kernels and targets of Artin transfers have recently turned out to be compatible with parent-descendant relations between finite p-groups and can favourably be used to endow descendant trees with additional structure.
References
[edit]- ^ a b c Newman, M. F. (1990). "Groups of prime-power order". Groups—Canberra 1989. Lecture Notes in Mathematics. Vol. 1456. Springer. pp. 49–62. doi:10.1007/bfb0100730. ISBN 978-3-540-53475-4.
- ^ a b Leedham-Green, C. R.; Newman, M. F. (1980). "Space groups and groups of prime power order I". Arch. Math. 35: 193–203. doi:10.1007/bf01235338. S2CID 121022964.
- ^ a b du Sautoy, M.; Segal, D. (2000). "Zeta functions of groups". New horizons in pro-p groups. Progress in Mathematics. Vol. 184. Basel: Birkhäuser. pp. 249–28.
- ^ Leedham-Green, C. R.; McKay, S. (2002). "The structure of groups of prime power order". London Mathematical Society Monographs. New Series. 27. Oxford University Press.
- ^ a b c d e Eick, B.; Leedham-Green, C. R.; Newman, M. F.; O'Brien, E. A. (2013). "On the classification of groups of prime-power order by coclass: the 3-groups of coclass 2". Int. J. Algebra Comput. 23 (5): 1243–1288. doi:10.1142/s0218196713500252.
- ^ a b c Newman, M. F.; O'Brien, E. A. (1999). "Classifying 2-groups by coclass". Trans. Amer. Math. Soc. 351: 131–169. doi:10.1090/s0002-9947-99-02124-8.
- ^ a b du Sautoy, M. (2001). "Counting p-groups and nilpotent groups". Inst. Hautes Études Sci. Publ. Math. 92: 63–112.
- ^ a b c Eick, B.; Leedham-Green, C. R. (2008). "On the classification of prime-power groups by coclass". Bull. London Math. Soc. 40 (2): 274–288. doi:10.1112/blms/bdn007.
- ^ Shalev, A. (1994). "The structure of finite p-groups: effective proof of the coclass conjectures". Invent. Math. 115: 315–345. Bibcode:1994InMat.115..315S. doi:10.1007/bf01231763. S2CID 122256486.
- ^ Leedham-Green, C. R. (1994). "The structure of finite p-groups". J. London Math. Soc. 50: 49–67. doi:10.1112/jlms/50.1.49.
- ^ Newman, M. F. (1977). Determination of groups of prime-power order. pp. 73-84, in: Group Theory, Canberra, 1975, Lecture Notes in Math., Vol. 573, Springer, Berlin.
- ^ O'Brien, E. A. (1990). "The p-group generation algorithm". J. Symbolic Comput. 9 (5–6): 677–698. doi:10.1016/s0747-7171(08)80082-x.
- ^ a b Besche, H. U.; Eick, B.; O'Brien, E. A. (2005). The SmallGroups Library – a library of groups of small order. An accepted and refereed GAP 4 package, available also in MAGMA.
- ^ Besche, H. U.; Eick, B.; O'Brien, E. A. (2002). "A millennium project: constructing small groups". Int. J. Algebra Comput. 12 (5): 623–644. doi:10.1142/s0218196702001115.
- ^ a b Ascione, J. A. (1979). On 3-groups of second maximal class. Ph. D. Thesis, Australian National University, Canberra.
- ^ Dietrich, Heiko; Eick, Bettina; Feichtenschlager, Dörte (2008), "Investigating p-groups by coclass with GAP", Computational group theory and the theory of groups, Contemporary Mathematics, vol. 470, Providence, RI: American Mathematical Society, pp. 45–61, doi:10.1090/conm/470/09185, ISBN 9780821843659, MR 2478413
- ^ Blackburn, N. (1958). "On a special class of p-groups". Acta Math. 100 (1–2): 45–92. doi:10.1007/bf02559602.
- ^ Taussky, O. (1937). "A remark on the class field tower". J. London Math. Soc. 12 (2): 82–85. doi:10.1112/jlms/s1-12.1.82.
- ^ a b Bagnera, G. (1898). "La composizione dei gruppi finiti il cui grado è la quinta potenza di un numero primo". Ann. Di Mat. (Ser. 3). 1: 137–228. doi:10.1007/bf02419191. S2CID 119799947.
- ^ a b Benjamin, E.; Lemmermeyer, F.; Snyder, C. (2003). "Imaginary quadratic fields with ". J. Number Theory. 103: 38–70. arXiv:math/0207307. doi:10.1016/S0022-314X(03)00084-2. S2CID 3124132.
- ^ Hall, M.; Senior, J. K. (1964). The groups of order . Macmillan, New York.
- ^ Hall, P. (1940). "The classification of prime-power groups". J. Reine Angew. Math. 182: 130–141.
- ^ Ascione, J. A.; Havas, G.; Leedham-Green, C. R. (1977). "A computer aided classification of certain groups of prime power order". Bull. Austral. Math. Soc. 17 (2): 257–274. doi:10.1017/s0004972700010467.
- ^ Nebelung, B. (1989). Klassifikation metabelscher 3-Gruppen mit Faktorkommutatorgruppe vom Typ (3,3) und Anwendung auf das Kapitulationsproblem. Inauguraldissertation, Universität zu Köln.









































































































































































































































































































