Disphenoid

The tetragonal and digonal disphenoids can be positioned inside a cuboid bisecting two opposite faces. All four faces are isosceles triangles. Both have four equal edges going around the sides. The digonal has two sets of isosceles triangle faces, while the tetragonal form has four identical isosceles triangle faces.

A rhombic disphenoid has 4 congruent scalene triangle faces, and can fit diagonally inside of a cuboid. It has three sets of edge lengths, existing as opposite pairs.

In geometry, a disphenoid is a tetrahedron whose four faces are congruent acute-angled triangles. It can also be described as a tetrahedron in which every two edges that are opposite each other have equal lengths. Other names are isosceles tetrahedron and equifacial tetrahedron. All the solid angles and vertex figures of a disphenoid are the same, and the sum of the face angles at each vertex is equal to two right angles. However, a disphenoid is not a regular polyhedron, because its faces are not regular polygons.

Special cases

The faces of a tetragonal disphenoid are isosceles; the faces of a rhombic disphenoid are scalene. If the faces are equilateral triangles, one obtains a regular tetrahedron, which is not normally considered a disphenoid.

Characterizations

A tetrahedron is a disphenoid if and only if its circumscribed parallelepiped is right-angled.

We also have that a tetrahedron is a disphenoid if and only if the center in the circumscribed sphere and the inscribed sphere coincide.

Another characterization states that if d₁, d₂ and d₃ are the common perpendiculars of AB and CD; AC and BD; and AD and BC respectively in a tetrahedron ABCD, then the tetrahedron is a disphenoid if and only if d₁, d₂ and d₃ are pairwise perpendicular.

Metric formulas

The volume of a disphenoid with opposite edges of length l, m and n is given by

$V=\sqrt{\frac{(l^2+m^2-n^2)(l^2-m^2+n^2)(-l^2+m^2+n^2)}{72}}.$

The circumscribed sphere has radius (the circumradius)

$R=\sqrt{\frac{l^2+m^2+n^2}{8}}$

and the inscribed sphere has radius

$r=\frac{3V}{4T}$

where V is the volume of the disphenoid and T is the area of any face, which is given by Heron's formula. There is also the following interesting relation connecting the volume and the circumradius:

$\displaystyle 16T^2R^2=l^2m^2n^2+9V^2.$

The square of the lengths of the bimedians are

$\tfrac{1}{2}(l^2+m^2-n^2),\quad \tfrac{1}{2}(l^2-m^2+n^2),\quad \tfrac{1}{2}(-l^2+m^2+n^2).$

Other properties

If the four faces of a tetrahedron have the same perimeter, then the tetrahedron is a disphenoid.

If the four faces of a tetrahedron have the same area, then it is a disphenoid.

The centers in the circumscribed and inscribed spheres coincide with the centroid of the disphenoid.

The bimedians are perpendicular to the edges they connect and to each other.

Honeycombs and crystals

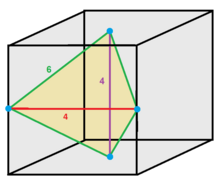
Some tetragonal disphenoids will form honeycombs. The disphenoid whose four vertices are (-1, 0, 0), (1, 0, 0), (0, 1, 1), and (0, 1, -1) is such a disphenoid. Each of its four faces is an isosceles triangle with edges of lengths √3, √3, and 2. It can tesselate space to form the disphenoid tetrahedral honeycomb. As Gibb describes, it can be folded without cutting or overlaps from a single sheet of a4 paper.

"Disphenoid" is also used to describe two forms of crystal:

• A wedge-shaped crystal form of the tetragonal or orthorhombic system. It has four triangular faces that are alike and that correspond in position to alternate faces of the tetragonal or orthorhombic dipyramid. It is symmetrical about each of three mutually perpendicular diad axes of symmetry in all classes except the tetragonal-disphenoidal, in which the form is generated by an inverse tetrad axis of symmetry.

• A crystal form bounded by eight scalene triangles arranged in pairs, constituting a tetragonal scalenohedron.

See also

• Orthocentric tetrahedron
• Snub disphenoid - A Johnson solid with 12 equilateral triangle faces and D_2d symmetry.
• Trirectangular tetrahedron

External links

• Weisstein, Eric W., "Disphenoid" from MathWorld.