Double-precision floating-point format
Double-precision floating-point format is a computer number format that occupies 8 bytes (64 bits) in computer memory and represents a wide, dynamic range of values by using a floating point.
Double-precision floating-point format usually refers to binary64, as specified by the IEEE 754 standard, not to the 64-bit decimal format decimal64. In older computers, different floating-point formats of 8 bytes were used, e.g., GW-BASIC's double-precision data type was the 64-bit MBF floating-point format.
| Floating-point formats |
|---|
| IEEE 754 |
|
| Other |
| Alternatives |
| Tapered floating point |
IEEE 754 double-precision binary floating-point format: binary64
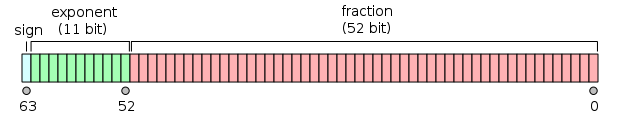
Double-precision binary floating-point is a commonly used format on PCs, due to its wider range over single-precision floating point, in spite of its performance and bandwidth cost. As with single-precision floating-point format, it lacks precision on integer numbers when compared with an integer format of the same size. It is commonly known simply as double. The IEEE 754 standard specifies a binary64 as having:
- Sign bit: 1 bit
- Exponent: 11 bits
- Significand precision: 53 bits (52 explicitly stored)
This gives from 15 to 17 significant decimal digits precision. If a decimal string with at most 15 significant digits is converted to IEEE 754 double-precision representation, and then converted back to a decimal string with the same number of digits, the final result should match the original string. If an IEEE 754 double-precision number is converted to a decimal string with at least 17 significant digits, and then converted back to double-precision representation, the final result must match the original number.[1]
The format is written with the significand having an implicit integer bit of value 1 (except for special data, see the exponent encoding below). With the 52 bits of the fraction significand appearing in the memory format, the total precision is therefore 53 bits (approximately 16 decimal digits, 53 log10(2) ≈ 15.955). The bits are laid out as follows:
The real value assumed by a given 64-bit double-precision datum with a given biased exponent and a 52-bit fraction is
or
Between 252=4,503,599,627,370,496 and 253=9,007,199,254,740,992 the representable numbers are exactly the integers. For the next range, from 253 to 254, everything is multiplied by 2, so the representable numbers are the even ones, etc. Conversely, for the previous range from 251 to 252, the spacing is 0.5, etc.
The spacing as a fraction of the numbers in the range from 2n to 2n+1 is 2n−52. The maximum relative rounding error when rounding a number to the nearest representable one (the machine epsilon) is therefore 2−53.
The 11 bit width of the exponent allows the representation of numbers between 10−308 and 10308, with full 15–17 decimal digits precision. By compromising precision, the subnormal representation allows even smaller values up to about 5 × 10−324.
Exponent encoding
The double-precision binary floating-point exponent is encoded using an offset-binary representation, with the zero offset being 1023; also known as exponent bias in the IEEE 754 standard. Examples of such representations would be:
e=000000000012=00116=1:
|
(smallest exponent for normal numbers) | ||
e=100000001012=40516=1029:
|
|||
e=111111111102=7fe16=2046:
|
(highest exponent) |
The exponents 00016 and 7ff16 have a special meaning:
00016is used to represent a signed zero (if F=0) and subnormals (if F≠0); and7ff16is used to represent ∞ (if F=0) and NaNs (if F≠0),
where F is the fractional part of the significand. All bit patterns are valid encoding.
Except for the above exceptions, the entire double-precision number is described by:
In the case of subnormals (e=0) the double-precision number is described by:
Double-precision examples
0 01111111111 00000000000000000000000000000000000000000000000000002 ≙ +20·1 = 1
|
0 01111111111 00000000000000000000000000000000000000000000000000012 ≙ +20·(1 + 2−52) ≈ 1.0000000000000002, the smallest number > 1
|
0 01111111111 00000000000000000000000000000000000000000000000000102 ≙ +20·(1 + 2−51) ≈ 1.0000000000000004
|
0 10000000000 00000000000000000000000000000000000000000000000000002 ≙ +21·1 = 2
|
1 10000000000 00000000000000000000000000000000000000000000000000002 ≙ −21·1 = −2
|
0 10000000000 10000000000000000000000000000000000000000000000000002 ≙ +21·1.12
|
= 112 = 3 |
0 10000000001 00000000000000000000000000000000000000000000000000002 ≙ +22·1
|
= 1002 = 4 |
0 10000000001 01000000000000000000000000000000000000000000000000002 ≙ +22·1.012
|
= 1012 = 5 |
0 10000000001 10000000000000000000000000000000000000000000000000002 ≙ +22·1.12
|
= 1102 = 6 |
0 10000000011 01110000000000000000000000000000000000000000000000002 ≙ +24·1.01112
|
= 101112 = 23 |
0 00000000000 00000000000000000000000000000000000000000000000000012
|
≙ +2−1022·2−52 = 2−1074 ≈ 4.9·10−324 |
(Min. subnormal positive double) |
0 00000000000 11111111111111111111111111111111111111111111111111112
|
≙ +2−1022·(1 − 2−52) ≈ 2.2250738585072009·10−308 |
(Max. subnormal double) |
0 00000000001 00000000000000000000000000000000000000000000000000002
|
≙ +2−1022·1 ≈ 2.2250738585072014·10−308 |
(Min. normal positive double) |
0 11111111110 11111111111111111111111111111111111111111111111111112
|
≙ +21023·(1 + (1 − 2−52)) ≈ 1.7976931348623157·10308 |
(Max. Double) |
0 00000000000 00000000000000000000000000000000000000000000000000002 ≙ +0
|
|
1 00000000000 00000000000000000000000000000000000000000000000000002 ≙ −0
|
|
0 11111111111 00000000000000000000000000000000000000000000000000002 ≙ +∞
|
(positive infinity) |
1 11111111111 00000000000000000000000000000000000000000000000000002 ≙ −∞
|
(negative infinity) |
0 11111111111 10000000000000000000000000000000000000000000000000002 ≙ NaN
|
|
0 11111111111 11111111111111111111111111111111111111111111111111112 ≙ NaN
|
(an alternative encoding) |
0 01111111101 01010101010101010101010101010101010101010101010101012 = 3fd5 5555 5555 555516
|
≙ +2−2·(1 + 2−2 + 2−4 + ... + 2−52) ≈ 1/3 |
By default, 1/3 rounds down, instead of up like single precision, because of the odd number of bits in the significand.
In more detail:
Given the hexadecimal representation 3FD5 5555 5555 555516,
Sign = 0
Exponent = 3FD16 = 1021
Exponent Bias = 1023 (constant value; see above)
Fraction = 5 5555 5555 555516
Value = 2(Exponent − Exponent Bias) × 1.Fraction – Note that Fraction must not be converted to decimal here
= 2−2 × (15 5555 5555 555516 × 2−52)
= 2−54 × 15 5555 5555 555516
= 0.333333333333333314829616256247390992939472198486328125
≈ 1/3
Execution speed with double-precision arithmetic
Using double-precision floating-point variables and mathematical functions (e.g., sin, cos, atan2, log, exp and sqrt) are slower than working with their single precision counterparts. One area of computing where this is a particular issue is for parallel code running on GPUs. For example, when using NVIDIA's CUDA platform, on video cards designed for gaming, calculations with double precision take 3 to 24 times longer to complete than calculations using single precision.[2]
Implementations
Doubles are implemented in many programming languages in different ways such as the following. On processors with only dynamic precision, such as x86 without SSE2 (or when SSE2 is not used, for compatibility purpose) and with extended precision used by default, software may have difficulties to fulfill some requirements.
C and C++
C and C++ offer a wide variety of arithmetic types. Double precision is not required by the standards (except by the optional annex F of C99, covering IEEE 754 arithmetic), but on most systems, the double type corresponds to double precision. However, on 32-bit x86 with extended precision by default, some compilers may not conform to the C standard and/or the arithmetic may suffer from double-rounding issues.[3]
Common Lisp
Common Lisp provides the types SHORT-FLOAT, SINGLE-FLOAT, DOUBLE-FLOAT and LONG-FLOAT. Most implementations provide SINGLE-FLOATs and DOUBLE-FLOATs with the other types appropriate synonyms. Common Lisp provides exceptions for catching floating-point underflows and overflows, and the inexact floating-point exception, as per IEEE 754. No infinities and NaNs are described in the ANSI standard, however, several implementations do provide these as extensions.
JavaScript
As specified by the ECMAScript standard, all arithmetic in JavaScript shall be done using double-precision floating-point arithmetic.[4]
Lua
In Lua version 5.2[5] and earlier, all arithmetic is done using double-precision floating-point arithmetic (explicit support for single-precision was added in version 5.3). Also, automatic type conversions between doubles and strings are provided (and also between floating-point values and integers since version 5.3).
See also
- IEEE floating point, IEEE standard for floating-point arithmetic (IEEE 754)
Notes and references
- ^ William Kahan (1 October 1997). "Lecture Notes on the Status of IEEE Standard 754 for Binary Floating-Point Arithmetic" (PDF).
- ^ http://www.tomshardware.com/reviews/geforce-gtx-titan-gk110-review,3438-3.html
- ^ GCC Bug 323 - optimized code gives strange floating point results
- ^ ECMA-262 ECMAScript Language Specification (PDF) (5th ed.). Ecma International. p. 29, §8.5 The Number Type.
- ^ http://www.lua.org/manual/5.2/manual.html