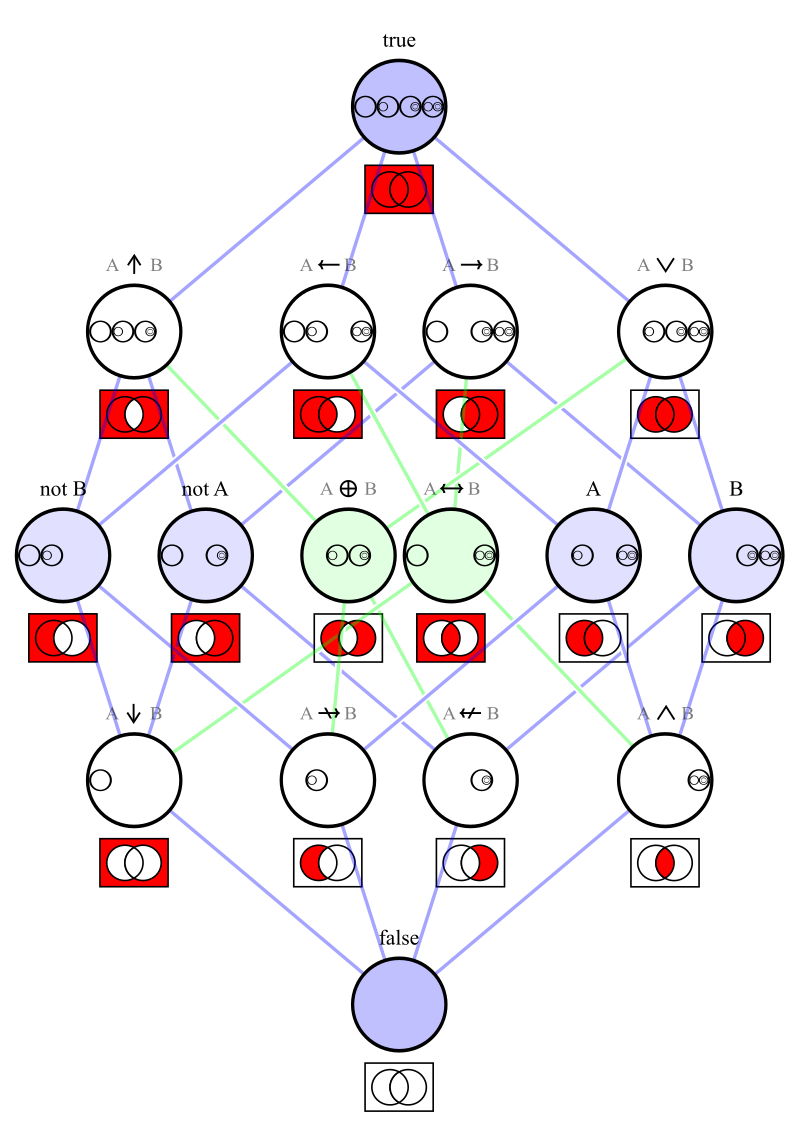
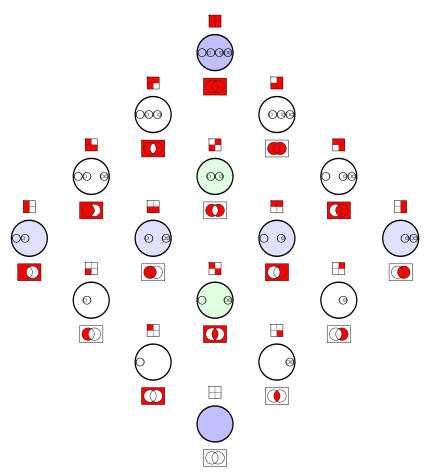
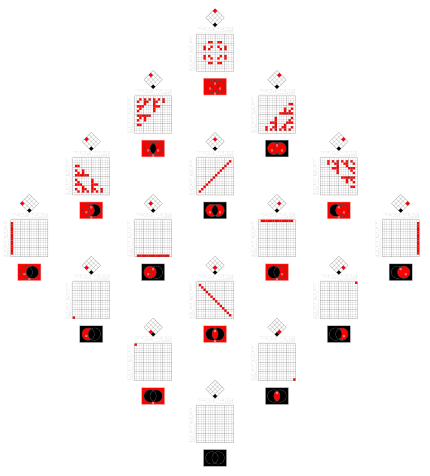
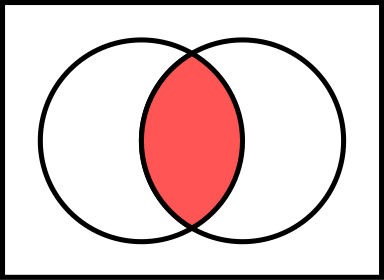
File:Venn0001.svg

From Wikipedia, the free encyclopedia
Jump to: navigation, search
Venn0001.svg‎ (SVG file, nominally 384 × 280 pixels, file size: 3 KB)

[edit] Summary

One of 16 Venn diagrams, representing 2-ary Boolean functions like set operations and logical connectives:

X or ¬X ¬A or ¬B A or ¬B ¬A or B A or B ¬B ¬A A xor B A xnor B A B ¬A and ¬B A and ¬B ¬A and B A and B X and ¬XLogical connectives Hasse diagram.svg
About this image


[edit] Operations and relations in set theory and logic

 
∅c		           
A = A
1111 1111
 
Ac \cup Bc		 true
A ↔ A		  
A \cup B		  
A \subseteq Bc		 A\LeftrightarrowA
 		  
A \supseteq Bc
1110 0111 1110 0111
 
A \cup Bc		 ¬A \or ¬B
A → ¬B		  
A \Delta B		 A \or B
A ← ¬B		  
Ac \cup B		  
A \supseteq B		 A\Rightarrow¬B
 		  
A = Bc		 A\Leftarrow¬B
 		  
A \subseteq B
1101 0110 1011 1101 0110 1011
 
Bc		 A \or ¬B
A ← B		  
A		 A \oplus B
A ↔ ¬B		  
Ac		 ¬A \or B
A → B		  
B		  
B = ∅		 A\LeftarrowB
 		  
A = ∅c		 A\Leftrightarrow¬B
 		  
A = ∅		 A\RightarrowB
 		  
B = ∅c
1100 0101 1010 0011 1100 0101 1010 0011
¬B
 		  
A \cap Bc		 A
 		  
(A \Delta B)c		 ¬A
 		  
Ac \cap B		 B
 		 B\Leftrightarrowfalse
 		 A\Leftrightarrowtrue
 		  
A = B		 A\Leftrightarrowfalse
 		 B\Leftrightarrowtrue
 
0100 1001 0010 0100 1001 0010
A \and ¬B
 		  
Ac \cap Bc		 A \leftrightarrow B
 		  
A \cap B		 ¬A \and B
 		 A\LeftrightarrowB
 
1000 0001 1000 0001
¬A \and ¬B
 		  
∅		 A \and B
 		  
A = Ac
0000 0000
false
A ↔ ¬A		 A\Leftrightarrow¬A
 
These sets or statements have complements
or negations. They are shown inside this matrix.		 These relations are statements, and have negations.
They are shown in a seperate matrix in the box below.



PD-icon.svg This file is ineligible for copyright and therefore in the public domain, because it consists entirely of information that is common property and contains no original authorship.

Afrikaans | العربية | ‪Беларуская (тарашкевіца)‬ | Български | Bosanski | Català | Česky | Dansk | Deutsch | English | Esperanto | Español | Eesti | فارسی | Suomi | Français | עברית | हिन्दी | Magyar | Հայերեն | Italiano | 日本語 | 한국어 | 文言 | Македонски | മലയാളം | Plattdüütsch | Nederlands | ‪Norsk (nynorsk)‬ | Polski | Português | Português do Brasil | Русский | Српски / Srpski | Svenska | ไทย | Türkçe | Vèneto | 中文 | ‪中文(简体)‬ | ‪中文(繁體)‬ | +/−

File history

Click on a date/time to view the file as it appeared at that time.

Date/TimeThumbnailDimensionsUserComment
current14:06, 26 July 2009Thumbnail for version as of 14:06, 26 July 2009384 × 280 (3 KB)Lipedia
14:05, 26 July 2009Thumbnail for version as of 14:05, 26 July 2009384 × 280 (3 KB)Lipedia
13:24, 26 January 2008Thumbnail for version as of 13:24, 26 January 2008615 × 463 (4 KB)Lipedia{{Information |Description= |Source=eigene arbeit |Date= |Author= Tilman Piesk |Permission= |other_versions= }}
15:57, 22 January 2008Thumbnail for version as of 15:57, 22 January 2008615 × 463 (4 KB)Lipedia{{Information |Description=Venn diagrams (sometimes called Johnston diagrams) concerning propositional calculus and set theory |Source=own work |Date=2008/Jan/22 |Author=Tilman Piesk |Permission=publich domain |other_versions= }}
14:26, 22 January 2008Thumbnail for version as of 14:26, 22 January 2008480 × 360 (3 KB)Lipedia{{Information |Description= |Source= |Date= |Author= |Permission= |other_versions= }}

Global file usage

The following other wikis use this file:

View more global usage of this file.

Metadata

This file contains additional information, probably added from the digital camera or scanner used to create or digitize it. If the file has been modified from its original state, some details may not fully reflect the modified file.
Width 384
Height 280
Retrieved from "http://en.wikipedia.org/wiki/File:Venn0001.svg"
Personal tools
Namespaces

Variants
Views
Actions
Navigation
Interaction
Toolbox