Wolf, goat and cabbage problem

The wolf, goat and cabbage problem is a river crossing puzzle. It dates back to at least the 9th century,[1] and has entered the folklore of several cultures.[2][3]
The story[edit]
A farmer with a wolf, a goat, and a cabbage must cross a river by boat. The boat can carry only the farmer and a single item. If left unattended together, the wolf would eat the goat, or the goat would eat the cabbage. How can they cross the river without anything being eaten?
Solution[edit]
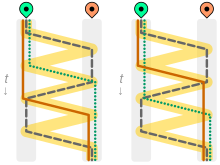
The first step that must be taken is to let the goat go across the river, as any other actions will result in the goat or the cabbage being eaten. When the farmer returns to the original side, he has the choice of taking either the wolf or the cabbage across next. If he takes the wolf across, he would have to return to get the cabbage, resulting in the wolf eating the goat. If he takes the cabbage across second, he will need to return to get the wolf, resulting in the cabbage being eaten by the goat. The dilemma is solved by taking the wolf (or the cabbage) over and bringing the goat back. Now he can take the cabbage (or the wolf) over, and finally return to fetch the goat.

His actions in the solution are summarized in the following steps:
- Take the goat over
- Return empty-handed
- Take the wolf or cabbage over
- Return with the goat
- Take whichever wasn't taken in step 3 over
- Return empty-handed
- Take the goat over
There are seven crossings: four forward and three back.
The key to the solution is realizing that one can bring things back (emphasized above). This is often unclear from the wording of the story, but never forbidden. Knowing this will make the problem easy to solve even by small children. The focus of the puzzle is not just task scheduling, but creative thinking, similarly to the Nine dots puzzle.

Occurrence and variations[edit]
The puzzle is one of a number of river crossing puzzles, where the object is to move a set of items across a river subject to various restrictions.
In the earliest known occurrence of this problem, in the medieval manuscript Propositiones ad Acuendos Juvenes, the three objects are a wolf, a goat, and a cabbage, but other cosmetic variations of the puzzle also exist, such as: wolf, sheep, and cabbage;[4][2], p. 26 fox, chicken, and grain;[5] fox, goose and corn;[6] and panther, pig, and porridge.[7] The logic of the puzzle, in which there are three objects, A, B, and C, such that neither A and B nor B and C can be left together, remains the same.
Another version of the puzzle stemming from a Chinese legend is recorded in an 18th-century painted panel by Japanese artist Maruyama Ōkyo, in the collection of the British museum. According to the legend, when a tiger has three cubs, one of them will be a leopard rather than a tiger, and more fierce than the others. Following this legend, the subject of a tiger with her cubs became a traditional subject for art in east Asia.[8] The depiction by Ōkyo shows the tiger family crossing a river, with the mother carrying one cub across the river at a time. This depicts a puzzle equivalent to the puzzle of the wolf, goat, and cabbage, asking how the mother can do this without leaving the leopard cub alone with any of the other tiger cubs.[9] The same variation of the puzzle has also been recorded as a koan of Ryōan-ji, a Zen temple in Kyoto.[10]
The puzzle has been found in the folklore of African-Americans, Cameroon, the Cape Verde Islands, Denmark, Ethiopia, Ghana, Italy, Romania, Russia, Scotland, the Sudan, Uganda, Zambia, and Zimbabwe.[2], pp. 26–27;[11] It has been given the index number H506.3 in Stith Thompson's motif index of folk literature, and is ATU 1579 in the Aarne–Thompson classification system.[12]
The puzzle was a favorite of Lewis Carroll,[13] and has been reprinted in various collections of recreational mathematics.[2], p. 26.
In his 'Arabian Nights' memoir, Meetings with Remarkable Men, the metaphysical Magus, G. I. Gurdjieff cites this riddle as "The Wolf, the goat and the cabbage". He notes, "This popular riddle clearly shows that...not solely by means of the ingenuity which every normal man should have, but that in addition he must not be lazy nor spare his strength, but must cross the river extra times for the attainment of his aim."
Variations of the puzzle also appear in the adventure game Broken Sword: The Sleeping Dragon, the Nintendo DS puzzle game Professor Layton and the Curious Village, and in The Simpsons episode "Gone Maggie Gone", where Homer has to get across a river with Maggie, Santa's Little Helper, and a jar of rat poison that looks like candy. In the Class of 3000 episode "Westley Side Story", Sunny and his students perform a similar exercise involving a chicken, a coyote and a sack of corn. The Between the Lions episode "Farmer Ken's Puzzle" portrays it being made into a computer game with a cat, a hen, and a sack of seeds.

In the Bull episode "Justice for Cable", Benny begins a riddle with "a man has a fox, a duck, and a bag of beans". Bull inexplicably declares "There is no answer", and everyone believes him.[14]
In some parts of Africa, variations on the puzzle have been found in which the boat can carry two objects instead of only one. When the puzzle is weakened in this way it is possible to introduce the extra constraint that no two items, including A and C, can be left together.[2], p. 27.
In the Star Trek: Prodigy episode "Time Amok", a holographic version of Kathryn Janeway employs the tale (here told as the chicken, fox and grain problem) to teach the crew of the USS Protostar how to work together.
See also[edit]
References[edit]
- ^ Pressman, Ian; David Singmaster (June 1989). ""The Jealous Husbands" and "The Missionaries and Cannibals"". The Mathematical Gazette. 73 (464). The Mathematical Association: 73–81. doi:10.2307/3619658. JSTOR 3619658. S2CID 116924808.
- ^ a b c d e Ascher, Marcia (February 1990). "A River-Crossing Problem in Cross-Cultural Perspective". Mathematics Magazine. 63 (1). Mathematical Association of America: 26–29. doi:10.2307/2691506. JSTOR 2691506.
- ^ Gurdjieff, G. I. (1963). Meetings with Remarkable Men (1st English ed.). London: Routledge & Kegan Paul. pp. 4–5.
- ^ Alcuin's Transportation Problems and Integer Programming Archived 2011-07-19 at the Wayback Machine, Ralf Borndörfer, Martin Grötschel, and Andreas Löbel, preprint SC-95-27 (November 1995), Konrad-Zuse-Zentrum für Informationstechnik Berlin.
- ^ The Classic River Crossing Puzzle Archived 2008-06-17 at the Wayback Machine
- ^ Mary Jane Sterling, Math Word Problems for Dummies, p. 313
- ^ Stewart, Ian (1998). The Magical Maze. Phoenix. ISBN 0-7538-0514-6.
- ^ Sung, Hou-Mei (2004). "Tiger with cubs: A rediscovered Ming court painting". Artibus Asiae. 64 (2): 281–293. JSTOR 3250187.
- ^ "A tiger's tale: British Museum buys rare Japanese screen". Art Fund. 20 October 2006. Retrieved 2021-01-08.
- ^ Goto, Seiko; Naka, Takahiro (2015). Japanese Gardens: Symbolism and Design. Routledge. p. 20. ISBN 9781317411642.
- ^ Evans-Pritchard, E. E. (1962). "235. Three Zande Texts". Man. 62: 149–152. doi:10.2307/2796709. JSTOR 2796709.
- ^ "Carrying a Wolf, a Goat, and a Cabbage across the Stream. Metamorphoses of ATU 1579", Piret Voolaid, Folklore: Electronic Journal of Folklore 35 (2007), pp. 111–130. Tartu: Eesti Kirjandusmuuseum.
- ^ p. 17, Rediscovered Lewis Carroll Puzzles, Lewis Carroll, compiled by Edward Wakeling, Courier Dover Publications, 1996, ISBN 0-486-28861-7.
- ^ "Springfield! Springfield!".
External links[edit]
- Goat, Cabbage and Wolf A Javascript simulation
- Fox, Chook and Corn A simulation without Javascript needed
