Free neutron decay
This article provides insufficient context for those unfamiliar with the subject. (January 2023) |
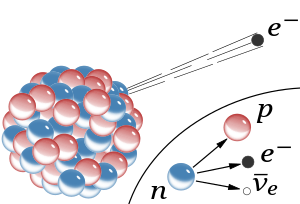
β−
radiation, the emission of a fast electron from the nucleus (the accompanying antineutrino is omitted). In the Rutherford model for the nucleus, red spheres were protons with positive charge and blue spheres were protons tightly bound to an electron with no net charge. : The inset shows beta decay of a free neutron as it is understood today; an electron and antineutrino are created in this process.
When embedded in an atomic nucleus, neutrons are (usually) stable particles. Outside the nucleus, free neutrons are unstable and have a mean lifetime of 877.75+0.50
−0.44 s[1] or 879.6±0.8 s[2] (about 14 min and 37.75 s or 39.6 s, respectively). Therefore, the half-life for this process (which differs from the mean lifetime by a factor of ln(2) ≈ 0.693) is 611±1 s (about 10 min, 11 s).[3][4]
The beta decay of the neutron described in this article can be notated at four slightly different levels of detail, as shown in four layers of Feynman diagrams in a section below.
The hard-to-observe
W−
quickly decays into an electron and its matching antineutrino. The subatomic reaction shown immediately above depicts the process as it was first understood, in the first half of the 20th century. The boson (
W−
) vanished so quickly that it was not detected until much later.
Later, beta decay was understood to occur by the emission of a weak boson (
W±
), sometimes called a charged weak current. Beta decay specifically involves the emission of a
W−
boson from one of the down quarks hidden within the neutron, thereby converting the down quark into an up quark and consequently the neutron into a proton. The following diagram gives a summary sketch of the beta decay process according to the present level of understanding.

| 3 quark composite neutron ( n0 ) |
3 quark composite proton ( p+ ) |
||||||
| ︷ | ︷ | ||||||
| ( u d d ) |
→ | ( u d u ) |
+ | W− |
|||
| ⤷ | e− |
+ ν e | |||||
| ︸ | |||||||
| subsequent W− decay | |||||||
- The down quark shown in bold (
d
) is nominally the one emitting the boson (
W−
) and thereby changing into an up quark (
u
), also in bold. The
u
d
quark pair not shown in bold are inert bystanders to the whole event.
For diagrams at several levels of detail, see § Decay process, below.
Energy budget[edit]
For the free neutron, the decay energy for this process (based on the rest masses of the neutron, proton and electron) is 0.782343 MeV. That is the difference between the rest mass of the neutron and the sum of the rest masses of the products. That difference has to be carried away as kinetic energy. The maximal energy of the beta decay electron (in the process wherein the neutrino receives a vanishingly small amount of kinetic energy) has been measured at 0.782±0.013 MeV.[5] The latter number is not well-enough measured to determine the comparatively tiny rest mass of the neutrino (which must in theory be subtracted from the maximal electron kinetic energy); furthermore, neutrino mass is constrained by many other methods.
A small fraction (about 1 in 1,000) of free neutrons decay with the same products, but add an extra particle in the form of an emitted gamma ray:
This gamma ray may be thought of as a sort of "internal bremsstrahlung" that arises as the emitted beta particle (electron) interacts with the charge of the proton in an electromagnetic way. In this process, some of the decay energy is carried away as photon energy. Gamma rays produced in this way are also a minor feature of beta decays of bound neutrons, that is, those within a nucleus.
A very small minority of neutron decays (about four per million) are so-called "two-body (neutron) decays", in which a proton, electron and antineutrino are produced as usual, but the electron fails to gain the 13.6 eV necessary energy to escape the proton (the ionization energy of hydrogen), and therefore simply remains bound to it, as a neutral hydrogen atom (one of the "two bodies"). In this type of free neutron decay, in essence all of the neutron decay energy is carried off by the antineutrino (the other "body").
The transformation of a free proton to a neutron (plus a positron and a neutrino) is energetically impossible, since a free neutron has a greater mass than a free proton. However, see proton decay.
Decay process viewed from multiple levels[edit]
Understanding of the beta decay process developed over several years, with the initial understanding of Enrico Fermi and colleagues starting at the "superficial" first level in the diagram below. Current understanding of weak processes rest at the fourth level, at the bottom of the chart, where the nucleons (the neutron and its successor proton) are largely ignored, and attention focuses only on the interaction between two quarks and a charged boson, with the decay of the boson almost treated as an afterthought. Because the charged weak boson (
W−
) vanishes so quickly, it was not actually observed during the first half of the 20th century, so the diagram at level 1 omits it; even at present it is for the most part inferred by its after-effects.
- 1 superficial BARYON level
n0
→
p+
+
e−
+
ν
eThe neutron (
n0
) emits an electron (
e−
) and its antineutrino (
ν
e) and becomes a proton (
p+
).2 deeper BOSON level
n0
→
p+
+
W−
The neutron (
n0
) emits a
W−
boson and becomes a proton (
p+
).⤷
e−
+
ν
eThe
W−
boson decays into an electron (
e−
) and its antineutrino (
ν
e).
(
u
d
d
)→ (
u
d
u
)+
W−
One of the down quarks in the neutron emits a
W−
boson and becomes an up quark.⤷
e−
+
ν
eThe
W−
boson decays into an electron (
e−
) and its antineutrino (
ν
e).
4 deepest QUARK level
d
→
u
+
W−
A down quark (
d
) emits a
W−
boson and becomes an up quark (
u
).⤷
e−
+
ν
eThe
W−
boson decays into an electron (
e−
) and its antineutrino (
ν
e).
Neutron lifetime puzzle[edit]
While the neutron lifetime has been studied for decades, there currently exists a lack of consilience on its exact value, due to different results from two experimental methods ("bottle" versus "beam"[6][a]). The "neutron lifetime anomaly" was discovered after the refinement of experiments with ultracold neutrons.[7] While the error margin was once overlapping, increasing refinement in technique which should have resolved the issue has failed to demonstrate convergence to a single value.[8][9][10][11] The difference in mean lifetime values obtained as of 2014 was approximately 9 seconds.[9] Further, a prediction of the value based on quantum chromodynamics as of 2018 is still not sufficiently precise to support one over the other.[12][b] As explained by Wolchover (2018),[6] the beam test would be incorrect if there is a decay mode that does not produce a proton.
On 13 October 2021 the lifetime from the bottle method was updated to [13][1] increasing the difference to 10 seconds below the beam method value of [14][15] and also on the same date a novel third method using data from the past NASA's Lunar prospector mission reported a value of [14][16] but with great uncertainty.
Yet another approach similar to the beam method has been explored with the Japan Proton Accelerator Research Complex (J-PARC) but it is too imprecise at the moment to be of significance on the analysis of the discrepancy.[17][18]
See also[edit]
- Halbach array-used in the "bottle" method
Footnotes[edit]
- ^ When physicists strip neutrons from atomic nuclei, put them in a bottle, then count how many remain there after some time, they infer that neutrons radioactively decay in 14m39s, on average. But when other physicists generate beams of neutrons and tally the emerging protons — the particles that free neutrons decay into — they peg the average neutron lifetime at around 14m48s. The discrepancy between the "bottle" and "beam" measurements has persisted [ever] since both methods of gauging the neutron's longevity began yielding results in the 1990s. At first, all the measurements were so imprecise that nobody worried. Gradually, though, both methods have improved, and still they disagree. — Wolchover (2018)[6]
- ^
The scientists have already used the new nucleon axial coupling calculation to derive a purely theoretical prediction of the lifetime of the neutron. Right now, this new value is consistent with the results from both types of experimental measurement, which differ by a mere 9sec.
- "We have a number for the neutron lifetime: 14m40s, with an error bar of 14s. That is right in the middle of the values measured by the two types of experiments, with an error bar that is big, and overlaps both,"
References[edit]
- ^ a b UCNτ Collaboration; Gonzalez, F. M.; Fries, E. M.; Cude-Woods, C.; Bailey, T.; Blatnik, M.; Broussard, L. J.; Callahan, N. B.; Choi, J. H.; Clayton, S. M.; Currie, S. A. (13 October 2021). "Improved Neutron Lifetime Measurement with UCNτ". Physical Review Letters. 127 (16): 162501. arXiv:2106.10375. doi:10.1103/PhysRevLett.127.162501. PMID 34723594. S2CID 235490073.
- ^ Particle Data Group (2020). Neutron mean life (Report). Review of Particle Physics. Berkeley, CA: Lawrence Berkeley Laboratory.
- ^ Beringer, J.; et al. (Particle Data Group) (2012). "Summary of baryons" (PDF). Phys. Rev. D. 86: 010001. doi:10.1103/PhysRevD.86.010001. S2CID 118588567.
- ^ Particle Data Group (2007). Summary Data Table on Baryons (PDF). lbl.gov (Report). Lawrence Berkeley Laboratory. Retrieved 16 August 2012.
- ^ Heyde, K. (2004). "Beta-decay: the weak interaction at work". Basic Ideas and Concepts in Nuclear Physics: An Introductory Approach (third ed.). Taylor & Francis. doi:10.1201/9781420054941. ISBN 978-0-7503-0980-6. Archived from the original on 19 January 2013 – via archive.today; link is to archived ch. 5 text.
- ^ a b c Wolchover, Natalie (13 February 2018). "Neutron lifetime puzzle deepens, but no dark matter seen". Quanta Magazine. Retrieved 31 July 2018.
- ^ Serebrov, A.P.; Fomin, A.K. (2011). "New evaluation of neutron lifetime from UCN storage experiments and beam experiments". Physics Procedia. 17: 199–205. arXiv:1104.4238. Bibcode:2011PhPro..17..199S. doi:10.1016/j.phpro.2011.06.037. S2CID 119204009.
- ^ Paul, Stephan (2009). "The puzzle of neutron lifetime". Nuclear Instruments and Methods in Physics Research Section A: Accelerators, Spectrometers, Detectors and Associated Equipment. 611 (2–3): 157–166. arXiv:0902.0169. Bibcode:2009NIMPA.611..157P. doi:10.1016/j.nima.2009.07.095. ISSN 0168-9002. S2CID 9765336.
- ^ a b Moskowitz, Clara (2014). "Neutron death mystery has physicists stymied". Nature. doi:10.1038/nature.2014.15219. ISSN 1476-4687. S2CID 123870434.
- ^ Greene, Geoffrey L.; Geltenbort, Peter (2016). "The Neutron Enigma". Scientific American. 314 (4): 36–41. Bibcode:2016SciAm.314d..36G. doi:10.1038/scientificamerican0416-36. ISSN 0036-8733. OSTI 1481712. PMID 27082189.
- ^ Mumm, Pieter (2018). "Resolving the neutron lifetime puzzle". Science. 360 (6389): 605–606. Bibcode:2018Sci...360..605M. doi:10.1126/science.aat7140. ISSN 0036-8075. PMID 29748273. S2CID 206667316.
- ^ a b "Nuclear scientists calculate value of key property that drives neutron decay". Brookhaven National Laboratory (Press release). 30 May 2018. Retrieved 31 July 2018.
- ^ "How Long Does a Neutron Live?". California Institute of Technology. 13 October 2021. Retrieved 14 October 2021.
- ^ a b Wilson, Jack T.; Lawrence, David J.; Peplowski, Patrick N.; Eke, Vincent R.; Kegerreis, Jacob A. (13 October 2021). "Measurement of the free neutron lifetime using the neutron spectrometer on NASA's Lunar Prospector mission". Physical Review C. 104 (4): 045501. arXiv:2011.07061. Bibcode:2021PhRvC.104d5501W. doi:10.1103/PhysRevC.104.045501. S2CID 226955795.
- ^ Anonymous (27 November 2013). "Discrepancy in Neutron Lifetime Still Unresolved". Physics. 6. Bibcode:2013PhyOJ...6S.150.. doi:10.1103/Physics.6.s150.
- ^ Lawrence, David J.; Wilson, Jack T.; Peplowski, Patrick N. (1 February 2021). "Space-based measurements of neutron lifetime: Approaches to resolving the neutron lifetime anomaly". Nuclear Instruments and Methods in Physics Research Section A: Accelerators, Spectrometers, Detectors and Associated Equipment. 988: 164919. arXiv:2011.06095. Bibcode:2021NIMPA.98864919L. doi:10.1016/j.nima.2020.164919. S2CID 226307043.
- ^ Hirota, K; Ichikawa, G; Ieki, S; Ino, T; Iwashita, Y; Kitaguchi, M; Kitahara, R; Koga, J; Mishima, K; Mogi, T; Morikawa, K (15 December 2020). "Neutron lifetime measurement with pulsed cold neutrons". Progress of Theoretical and Experimental Physics. 2020 (12): 123C02. arXiv:2007.11293. doi:10.1093/ptep/ptaa169. ISSN 2050-3911.
- ^ "KEK tackles neutron-lifetime puzzle". CERN Courier. 2 July 2021. Retrieved 2 December 2021.
Bibliography[edit]
- Ерозолимский, Б.Г. (1975). "Beta decay of the neutron" Бета-распад нейтрона [Neutron beta decay]. Успехи Физических Наук Успехи физических наук. 116 (1): 145–164. doi:10.3367/UFNr.0116.197505e.0145.



