Free spectral range
This article needs additional citations for verification. (August 2017) |
Free spectral range (FSR) is the spacing in optical frequency or wavelength between two successive reflected or transmitted optical intensity maxima or minima of an interferometer or diffractive optical element.[1]
The FSR is not always represented by or , but instead is sometimes represented by just the letters FSR. The reason is that these different terms often refer to the bandwidth or linewidth of an emitted source respectively.
In general[edit]
The free spectral range (FSR) of a cavity in general is given by [2]
or, equivalently,
These expressions can be derived from the resonance condition by expanding in Taylor series. Here, is the wavevector of the light inside the cavity, and are the wavevector and wavelength in vacuum, is the refractive index of the cavity and is the round trip length of the cavity (notice that for a standing-wave cavity, is equal to twice the physical length of the cavity).
Given that , the FSR (in wavelength) is given by
being is the group index of the media within the cavity. or, equivalently,
where is the speed of light in vacuum.
If the dispersion of the material is negligible, i.e. , then the two expressions above reduce to
and
A simple intuitive interpretation of the FSR is that it is the inverse of the roundtrip time :
In wavelength, the FSR is given by
where is the vacuum wavelength of light. For a linear cavity, such as the Fabry-Pérot interferometer[3] discussed below, , where is the distance travelled by light in one roundtrip around the closed cavity, and is the length of the cavity.
Diffraction gratings[edit]
The free spectral range of a diffraction grating is the largest wavelength range for a given order that does not overlap the same range in an adjacent order. If the (m + 1)-th order of and m-th order of lie at the same angle, then
Fabry–Pérot interferometer[edit]
In a Fabry–Pérot interferometer[3] or etalon, the wavelength separation between adjacent transmission peaks is called the free spectral range of the etalon and is given by
where λ0 is the central wavelength of the nearest transmission peak, n is the index of refraction of the cavity medium, is the angle of incidence, and is the thickness of the cavity. More often FSR is quoted in frequency, rather than wavelength units:
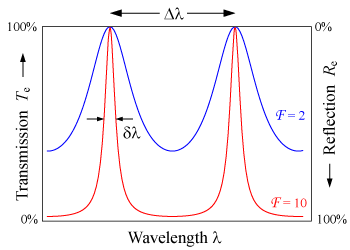
The FSR is related to the full-width half-maximum δλ of any one transmission band by a quantity known as the finesse:
where is the coefficient of finesse, and R is the reflectivity of the mirrors.
This is commonly approximated (for R > 0.5) by
References[edit]
- ^ Hecht, Eugene (2017). Optics (5th ed.). pp. 431–433, 614. ISBN 9780133977226. OCLC 953709783.
- ^ Rabus, Dominik.G. (26 April 2007). Integrated Ring Resonators. ISBN 978-3-540-68788-7. OCLC 123893382.
- ^ a b Ismail, N.; Kores, C. C.; Geskus, D.; Pollnau, M. (2016). "Fabry-Pérot resonator: spectral line shapes, generic and related Airy distributions, linewidths, finesses, and performance at low or frequency-dependent reflectivity". Optics Express. 24 (15): 16366–16389. Bibcode:2016OExpr..2416366I. doi:10.1364/OE.24.016366. PMID 27464090.












![{\displaystyle \left|\left({\frac {\partial \beta }{\partial \lambda }}\right)\right|={\frac {2\pi }{\lambda ^{2}}}\left[n(\lambda )-\lambda {\frac {\partial n}{\partial \lambda }}\right]={\frac {2\pi }{\lambda ^{2}}}n_{g}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/94bc7f13a49a62045f7002396deacd797e7fa47d)


















