Halin graph
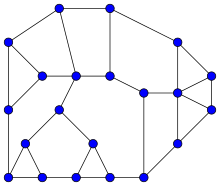
In graph theory, a mathematical discipline, a Halin graph is a planar graph constructed from a plane embedding of a tree with at least four vertices and with no vertices of degree 2, by connecting all the leaves of the tree (the vertices of degree 1) with a cycle that passes around the tree in the natural cyclic order defined by the embedding of the tree.[1] Halin graphs are named after German mathematician Rudolf Halin, who studied them in 1971,[2] but the cubic Halin graphs had already been studied over a century earlier by Kirkman.[3]
Construction
A Halin graph is constructed as follows. Let be a tree with at least tree vertices such that no vertex of has degree 2. Moreover assume has leaves. Then a Halin graph is constructed by creating a cycle thorough the leaves of such that the obtained graph is planar.
Examples
Every wheel graph (the graph of a pyramid) is a Halin graph, whose tree is a star. The graph of a triangular prism is also a Halin graph; it can be drawn so that one of its rectangular faces is the exterior cycle, and the remaining edges form a tree with four leaves, two interior vertices, and five edges.
The Frucht graph, one of the two smallest cubic graphs with no nontrivial graph automorphisms, is also a Halin graph.
Properties
- Every Halin graph is an edge-minimal planar 3-connected graph,[1] and therefore by Steinitz's theorem it is a polyhedral graph.
- Every Halin graph has a unique planar embedding (up to the choice of the outer space; i.e., a unique embedding onto a 2-sphere).[1]
- Every Halin graph is a Hamiltonian graph, and every edge of the graph belongs to a Hamiltonian cycle. Moreover, any Halin graph remains Hamiltonian after deletion of any vertex.[4]
- Every Halin graph is almost pancyclic, in the sense that it has cycles of all lengths from 3 to n with the possible exception of a single even length. Moreover, any Halin graph remains almost pancyclic if a single edge is contracted, and every Halin graph without interior vertices of degree three is pancyclic.[5]
- Every Halin graph has treewidth at most three;[6] therefore, many graph optimization problems that are NP-complete for arbitrary planar graphs, such as finding a maximum independent set, may be solved in linear time on Halin graphs using dynamic programming.[7]
- Because every tree without vertices of degree 2 contains two leaves that share the same parent, every Halin graph contains a triangle. In particular, it is not possible for a Halin graph to be a triangle-free graph nor a bipartite graph.
- The weak dual of a Halin graph (the graph whose vertices correspond to bounded faces of the Halin graph, and whose edges correspond to adjacent faces) is biconnected and outerplanar. A planar graph is a Halin graph if and only if its weak dual is biconnected and outerplanar.[8]
History
In 1971, Halin introduced the Halin graphs as a class of minimally 3-vertex-connected graphs: for every edge in the graph, the removal of that edge reduces the connectivity of the graph.[2] These graphs gained in significance with the discovery that many algorithmic problems that were computationally infeasible for arbitrary planar graphs could be solved efficiently on them,[4][8] a fact that was later explained to be a consequence of their low treewidth.[6][7]
Prior to Halin's work on these graphs, graph enumeration problems concerning the cubic Halin graphs were studied in 1965 by Hans Rademacher.[9] Rademacher defines these graphs (which he calls based polyhedra) as the cubic polyhedral graphs in which one of the faces has f − 1 sides, where f is the number of faces of the polyhedron, and he points to much earlier work published in 1856 by Thomas Kirkman on the same class of graphs.[3]
The Halin graphs are sometimes also called roofless polyhedra,[4] but, like "based polyhedra", this name may also refer to the cubic Halin graphs.[10]
References
- ^ a b c Encyclopaedia of Mathematics, first Supplementary volume, 1988, ISBN 0-7923-4709-9, p. 281, article "Halin Graph", and references therein.
- ^ a b Halin, R. (1971), "Studies on minimally n-connected graphs", Combinatorial Mathematics and its Applications (Proc. Conf., Oxford, 1969), London: Academic Press, pp. 129–136, MR 0278980.
- ^ a b Kirkman, Th. P. (1856), "On the enumeration of x-edra having triedral summits and an (x − 1)-gonal base", Philosophical Transactions of the Royal Society of London: 399–411, JSTOR 108592.
- ^ a b c Cornuéjols, G.; Naddef, D.; Pulleyblank, W. R. (1983), "Halin graphs and the travelling salesman problem", Mathematical Programming, 26 (3): 287–294, doi:10.1007/BF02591867.
- ^ Skowrońska, Mirosława (1985), "The pancyclicity of Halin graphs and their exterior contractions", in Alspach, Brian R.; Godsil, Christopher D. (eds.), Cycles in Graphs, Annals of Discrete Mathematics, vol. 27, Elsevier Science Publishers B.V., pp. 179–194.
- ^ a b Bodlaender, Hans (1988), Planar graphs with bounded treewidth (PDF), Technical Report RUU-CS-88-14, Department of Computer Science, Utrecht University.
- ^ a b Bodlaender, Hans (1988), "Dynamic programming on graphs with bounded treewidth", Proceedings of the 15th International Colloquium on Automata, Languages and Programming, Lecture Notes in Computer Science, vol. 317, Springer-Verlag, pp. 105–118.
- ^ a b Sysło, Maciej M.; Proskurowski, Andrzej (1983), "On Halin graphs", Graph Theory: Proceedings of a Conference held in Lagów, Poland, February 10–13, 1981, Lecture Notes in Mathematics, vol. 1018, Springer-Verlag, pp. 248–256, doi:10.1007/BFb0071635.
- ^ Rademacher, Hans (1965), "On the number of certain types of polyhedra", Illinois Journal of Mathematics, 9: 361–380, MR 0179682.
- ^ Lovász, L.; Plummer, M. D. (1974), "On a family of planar bicritical graphs", Combinatorics (Proc. British Combinatorial Conf., Univ. Coll. Wales, Aberystwyth, 1973), London: Cambridge Univ. Press, pp. 103–107. London Math. Soc. Lecture Note Ser., No. 13, MR 0351915.
External links
- Halin graphs, Information System on Graph Class Inclusions.
- Weisstein, Eric W. "Halin Graph". MathWorld.


