Hash table

In computer science, a hash table, or a hash map, is a data structure that associates keys with values. The primary operation it supports efficiently is a lookup: given a key (e.g. a person's name), find the corresponding value (e.g. that person's telephone number). It works by transforming the key using a hash function into a hash, a number that the hash table uses to locate the desired value.

Hash tables are often used to implement associative arrays, sets and caches. Like arrays, hash tables provide constant-time O(1) lookup on average, regardless of the number of items in the table. However, the rare worst-case lookup time can be as bad as O(n). Compared to other associative array data structures, hash tables are most useful when large numbers of records of data are to be stored.

Hash tables store data in pseudo-random locations, so accessing the data in a sorted manner is a very time consuming operation. Other data structures such as self-balancing binary search trees generally operate more slowly (since their lookup time is O(log n)) and are rather more complex to implement than hash tables but maintain a sorted data structure at all times. See a comparison of hash tables and self-balancing binary search trees.

Overview

The basic operations that hash tables generally support are:

insert(key, value)

lookup(key) which returns value

Most, but not all hash tables support delete(key). Other services like iterating over the table, growing the table, emptying the table may be provided. Some hash tables allow multiple values to be stored under the same key. Other types of hash table only pass a single value representing both the key/data or even just a key, depending on what the hash table is to be used for.

Keys may be pretty much anything, a number, a string, an object; with some hash tables even a reference to the value being stored. The only requirement is the existence of a hash function for the keys used (see below).

Hash tables use an array, which is sometimes confusingly also called the hash table. Each element of the array, also called a slot or bucket, can contain one key–value pair, or record.

Because the number of valid keys is typically much larger than the range of valid indexes into the array, a way is needed to convert each key into a valid index. This is achieved using a hash function which is a function that takes a key and returns an index into an array. The indexed element of the array, in turn, should contain the record that is associated to that key.

However, when there are more potential keys than array indexes, it can be shown (by the pigeonhole principle) that two or more potential keys will have the same hash; this is called a collision. The hash function should be designed so as to minimise the number of collisions for any index returned.

Because multiple keys can map to each array slot, we need a collision resolution strategy, whose function is to find a place to store a new key if the slot is already occupied. For example, the colliding record may be inserted in the next free array slot, or we can have each array slot refer to a linked list of records.

Even though some collisions occur, with good hash functions and when the table is up to around 80% full, collisions are relatively rare and performance is very good, as very few comparisons will be made on average. However, if the table becomes too full, performance becomes poor, and the hash table's array must be enlarged. Enlarging the table (see the Table resizing section) means that effectively all the records in the hash table have to be added all over again.

Most implementations of hash tables are not persistent data structures, in the sense that there is no way to update them while retaining access to the previous copy of the hash table (although they often are persistent in the sense of disk-based). Some implementations of hash tables, such as those using a VList, are persistent, but these are rarely used in practice and are not as efficient as normal hash tables due to increased indexing time.

Common uses of hash tables

Hash tables are commonly used for symbol tables, caches, and sets.

Hash tables are not, generally speaking, persistent data structures, in the sense that there is no simple space-efficient way to update a hash table while retaining access to the previous copy of the hash table. Hash tables may be "persistent" in the other sense of the word, meaning disk-based; database indexes commonly use disk-based data structures based on hash tables.

In computer chess, a hash table is generally used to implement the transposition table.

Choosing a good hash function

A good hash function is essential for good hash table performance. Hash collisions are generally resolved by some form of linear search, so if a hash function tends to produce similar values, slow searches will result.

In an ideal hash function, changing any single bit in the key (including extending or shortening the key) would change half the bits of the hash, and this change would be independent of the changes caused by any other bits of the key. Because a good hash function can be hard to design, or computationally expensive to execute, much research has been devoted to collision resolution strategies that mitigate poor hashing performance. However, none of them is as effective as using a good hash function in the first place.

It is desirable to use the same hash function for arrays of any conceivable size. To do this, the index into the hash table's array is generally calculated in two steps:

A generic hash value is calculated which fills a natural machine integer
This value is reduced to a valid array index by finding its modulus with respect to the array's size.

Hash table array sizes are sometimes chosen to be prime numbers. This is done to avoid any tendency for the large integer hash to have common divisors with the hash table size, which would otherwise induce collisions after the modulus operation. However, a prime table size is no substitute for a good hash function.

A common alternative to prime sizes is to use a size which is a power of two, with simple bit masking to achieve the modulus operation. Such bit masking may be significantly computationally cheaper than the division operation. In either case it is often a good idea to arrange the generic hash value to be constructed using prime numbers that share no common divisors (i.e. is coprime) with the table length.

One surprisingly common problem that can occur with hash functions is clustering. Clustering occurs when the structure of the hash function causes commonly used keys to tend to fall closely spaced or even consecutively within the hash table. This can cause significant performance degradation as the table fills when using certain collision resolution strategies, such as linear probing.

When debugging the collision handling in a hash table, it is sometimes useful to use a hash function that always returns a constant value, such as 1, which causes collisions on almost every insert.

In environments where an adversary may attempt to force the algorithm to run slowly by supplying bad input, a good solution is universal hashing, a scheme where we randomly select a hash function at the beginning of the algorithm. Because the adversary doesn't know which hash function we're using, they don't know what input is "bad".

Collision resolution

If two keys hash to the same index, the corresponding records cannot be stored in the same location. So, if it's already occupied, we must find another location where to store the new record, and do it so that we can find it when we look it up later on.

To give an idea of the importance of a good collision resolution strategy, consider the following result, derived using the birthday paradox. Even if we assume that our hash function outputs random indices uniformly distributed over the array, and even for an array with 1 million entries, there is a 95% chance of at least one collision occurring before it contains 2500 records.

There are a number of collision resolution techniques, but the most popular are chaining and open addressing.

Chaining

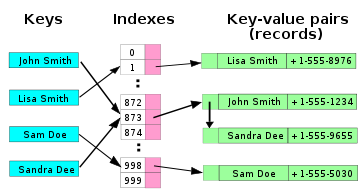
In the simplest chained hash table technique, each slot in the array references a linked list of inserted records that collide to the same slot. Insertion requires finding the correct slot, and appending to either end of the list in that slot; deletion requires searching the list and removal.

Chaining hash tables have advantages over open addressed hash tables in that the removal operation is simple and resizing the table can be postponed for a much longer time because performance degrades more gracefully even when every slot is used. Indeed, many chaining hash tables may not require resizing at all since performance degradation is linear as the table fills. For example, a chaining hash table containing twice its recommended capacity of data would only be about twice as slow on average as the same table at its recommended capacity.

Chained hash tables inherit the disadvantages of linked lists. When storing small records, the overhead of the linked list can be significant. An additional disadvantage is that traversing a linked list has poor cache performance.

Alternative data structures can be used for chains instead of linked lists. By using a self-balancing tree, for example, the theoretical worst-case time of a hash table can be brought down to O(log n) rather than O(n). However, since each list is intended to be short, this approach is usually inefficient unless the hash table is designed to run at full capacity or there are unusually high collision rates, as might occur in input designed to cause collisions. Dynamic arrays can also be used to decrease space overhead and improve cache performance when records are small.

Some chaining implementations use an optimization where the first record of each chain is stored in the table. Although this can increase performance, it is generally not recommended: chaining tables with reasonable load factors contain a large proportion of empty slots, and the larger slot size causes them to waste large amounts of space.

Open addressing

Hash collision resolved by linear probing (interval=1).

Open addressing hash tables can store the records directly within the array. A hash collision is resolved by probing, or searching through alternate locations in the array (the probe sequence) until either the target record is found, or an unused array slot is found, which indicates that there is no such key in the table. Well known probe sequences include:

linear probing: in which the interval between probes is fixed--often at 1,
quadratic probing: in which the interval between probes increases linearly (hence, the indices are described by a quadratic function), and
double hashing: in which the interval between probes is fixed for each record but is computed by another hash function.

The main tradeoffs between these methods is that linear probing has the best cache performance but is most sensitive to clustering, while double hashing has poor cache performance but exhibits virtually no clustering; quadratic hashing falls in-between in both areas. Double hashing can also require more computation than other forms of probing.

A critical influence on performance of an open addressing hash table is the load factor; that is, the proportion of the slots in the array that are used. As the load factor increases towards 100%, the number of probes that may be required to find or insert a given key rises dramatically. Once the table becomes full, probing algorithms may even fail to terminate. Even with good hash functions, load factors are normally limited to 80%. A poor hash function can exhibit poor performance even at very low load factors by generating significant clustering. What causes hash functions to cluster is not well understood, and it is easy to unintentionally write a hash function which causes severe clustering.

Open addressing versus chaining

Chained hash tables have the following benefits over open addressing:

They are simple to implement effectively and only require basic data structures.
From the point of view of writing suitable hash functions, chained hash tables are insensitive to clustering, only requiring minimization of collisions. Open addressing depends upon better hash functions to avoid clustering. This is particularly important if novice programmers can add their own hash functions, but even experienced programmers can be caught out by unexpected clustering effects.
They degrade in performance more gracefully. Although chains grow longer as the table fills, a chained hash table cannot "fill up" and does not exhibit the sudden increases in lookup times that occur in a near-full table with open addressing. (see right)
If the hash table stores large records, about 5 or more words per record, chaining uses less memory then open addressing.
If the hash table is sparse (that is, it has a big array with many free array slots), chaining uses less memory than open addressing even for small records of 2 to 4 words per record due to its external storage.

For small record sizes (a few words or less) the benefits of in-place open addressing compared to chaining are:

They can be more space-efficient than chaining since they don't need to store any pointers or allocate any additional space outside the hash table. Simple linked lists require a word of overhead per element.
Insertions avoid the time overhead of memory allocation, and can even be implemented in the absence of a memory allocator.
Because it uses internal storage, open addressing avoids the extra indirection required for chaining's external storage. It also has better locality of reference, particularly with linear probing. With small record sizes, these factors can yield better performance than chaining, particularly for lookups.
They can be easier to serialize, because they don't use pointers.

On the other hand, normal open addressing is a poor choice for large elements, since these elements fill entire cache lines (negating the cache advantage), and a large amount of space is wasted on large empty table slots. If the open addressing table only stores references to elements (external storage), it uses space comparable to chaining even for large records but loses its speed advantage.

Generally speaking, open addressing is better used for hash tables with small records that can be stored within the table (internal storage) and fit in a cache line. They are particularly suitable for elements of one word or less. In cases where the tables are expected to have high load factors, the records are large, or the data is variable-sized, chained hash tables often perform as well or better.

Ultimately, used sensibly any kind of hash table algorithm is usually fast enough; and the percentage of a calculation spent in hash table code is low. Memory usage is rarely considered excessive. Therefore, in most cases the differences between these algorithms is marginal, and other considerations typically come into play.

Coalesced hashing

A hybrid of chaining and open addressing, coalesced hashing links together chains of nodes within the table itself. Like open addressing, it achieves space usage and (somewhat diminished) cache advantages over chaining. Like chaining, it does not exhibit clustering effects; in fact, the table can be efficiently filled to a high density. Unlike chaining, it cannot have more elements than table slots.

Perfect hashing

If all of the keys that will be used are known ahead of time, and there are no more keys that can fit the hash table, perfect hashing can be used to create a perfect hash table, in which there will be no collisions. If minimal perfect hashing is used, every location in the hash table can be used as well.

Probabilistic hashing

Perhaps the simplest solution to a collision is to replace the value that is already in the slot with the new value, or slightly less commonly, drop the record that is to be inserted. In later searches, this may result in a search not finding a record which has been inserted. This technique is particularly useful for implementing caching.

An even more space-efficient solution which is similar to this is use a bit array (an array of one-bit fields) for our table. Initially all bits are set to zero, and when we insert a key, we set the corresponding bit to one. False negatives cannot occur, but false positives can, since if the search finds a 1 bit, it will claim that the value was found, even if it was just another value that hashed into the same array slot by coincidence. In reality, such a hash table is merely a specific type of Bloom filter.

Table resizing

With a good hash function, a hash table can typically contain about 70%–80% as many elements as it does table slots and still perform well. Depending on the collision resolution mechanism, performance can begin to suffer either gradually or dramatically as more elements are added. To deal with this, when the load factor exceeds some threshold, we allocate a new, larger table, and add all the contents of the original table to this new table. In Java's HashMap class, for example, the default load factor threshold is 0.75.

This can be a very expensive operation, and the necessity for it is one of the hash table's disadvantages. In fact, some naive methods for doing this, such as enlarging the table by one each time you add a new element, reduce performance so drastically as to make the hash table useless. However, if we enlarge the table by some fixed percent, such as 10% or 100%, it can be shown using amortized analysis that these resizings are so infrequent that the average time per lookup remains constant-time. To see why this is true, suppose a hash table using chaining begins at the minimum size of 1 and is doubled each time it fills above 100%. If in the end it contains n elements, then the total add operations performed for all the resizings is:

1 + 2 + 4 + ... + n = 2n - 1.

Because the costs of the resizings form a geometric series, the total cost is O(n). But we also perform n operations to add the n elements in the first place, so the total time to add n elements with resizing is O(n), an amortized time of O(1) per element.

On the other hand, some hash table implementations, notably in real-time systems, cannot pay the price of enlarging the hash table all at once, because it may interrupt time-critical operations. One simple approach is to initially allocate the table with enough space for the expected number of elements and forbid the addition of too many elements. Another useful but more memory-intensive technique is to perform the resizing gradually:

Allocate the new hash table, but leave the old hash table and check both tables during lookups.
Each time an insertion is performed, add that element to the new table and also move k elements from the old table to the new table.
When all elements are removed from the old table, deallocate it.

To ensure that the old table will be completely copied over before the new table itself needs to be enlarged, it's necessary to increase the size of the table by a factor of at least (k + 1)/k during the resizing.

Another way to decrease the cost of table resizing is to choose a hash function in such a way that the hashes of most values do not change when the table is resized. This approach, called consistent hashing, is prevalent in disk-based and distributed hashes, where resizing is prohibitively costly.

Example pseudocode

The following pseudocode is an implementation of an open addressing hash table with linear probing and single-slot stepping, a common approach that is effective if the hash function is good. Each of the lookup, set and remove functions use a common internal function findSlot to locate the array slot that either does or should contain a given key.

 record pair { key, value }
 var pair array slot[0..numSlots-1]
 
 function findSlot(key)
     i := hash(key) modulus numSlots
     loop
         if slot[i] is not occupied or slot[i].key = key
             return i
         i := (i + 1) modulus numSlots
 
 function lookup(key)
     i := findSlot(key)
     if slot[i] is occupied   // key is in table
         return slot[i].value
     else                     // key is not in table
         return not found     
 
 function set(key, value)
     i := findSlot(key)
     if slot[i] is occupied
         slot[i].value := value
     else
         if the table is almost full
             rebuild the table larger (note 1)
             i := findSlot(key)
         slot[i].key   := key
         slot[i].value := value

note 1: Rebuilding the table requires allocating a larger array and recursively using the set operation to insert all the elements of the old array into the new larger array. It is common to increase the array size exponentially, for example by doubling the old array size.

 function remove(key)
     i := findSlot(key)
     if slot[i] is unoccupied
         return   // key is not in the table
     j := i
     loop
         j := (j+1) modulus numSlots
         if slot[j] is unoccupied
             exit loop
         k := hash(slot[j].key) modulus numSlots
         if (j > i and (k <= i or k > j)) or
            (j < i and (k <= i and k > j)) (note 2)
             slot[i] := slot[j]
             i := j
     mark slot[i] as unoccupied

note 2: For all records in a cluster, there must be no vacant slots between their natural hash position and their current position (else lookups will terminate before finding the record). At this point in the pseudocode, i is a vacant slot that might be invalidating this property for subsequent records in the cluster. j is such as subsequent record. k is the raw hash where the record at j would naturally land in the hash table if there were no collisions. This test is asking if the record at j is invalidly positioned with respect to the required properties of a cluster now that i is vacant.

Another technique for removal is simply to mark the slot as deleted. However this eventually requires rebuilding the table simply to remove deleted records. The methods above provide O(1) updating and removal of existing records, with occasional rebuilding if the high water mark of the table size grows.

The O(1) remove method above is only possible in linearly probed hash tables with single-slot stepping. In the case where many records are to be deleted in one operation, marking the slots for deletion and later rebuilding may be more efficient.

Problems with hash tables

Although hash table lookups use constant time on average, the time spent can be significant. Evaluating a good hash function can be a slow operation. In particular, if simple array indexing can be used instead, this is usually faster.

Hash tables in general exhibit poor locality of reference—that is, the data to be accessed is distributed seemingly at random in memory. Because hash tables cause access patterns that jump around, this can trigger microprocessor cache misses that cause long delays (see CPU cache). Compact data structures such as arrays, searched with linear search, may be faster if the table is relatively small and keys are cheap to compare, such as with simple integer keys. Due to Moore's Law, cache sizes are growing exponentially and so what is considered "small" may be increasing. The optimum performance point varies from system to system; for example, a trial on Parrot shows that its hash tables outperform linear search in all but the most trivial cases (one to three entries).

More significantly, hash tables are more difficult and error-prone to write and use. Hash tables require the design of an effective hash function for each key type, which in many situations is more difficult and time-consuming to design and debug than the mere comparison function required for a self-balancing binary search tree. In open-addressed hash tables it's even easier to create a poor hash function.

Additionally, in some applications, a black hat with knowledge of the hash function may be able to supply information to a hash which creates worst-case behavior by causing excessive collisions, resulting in very poor performance (i.e., a denial of service attack). In critical applications, a data structure with better worst-case guarantees may be preferable. For details, see Crosby and Wallach's Denial of Service via Algorithmic Complexity Attacks.

Implementations

While many programming languages already provide hash table functionality (see language support for associative arrays), there are several independent implementations worth mentioning.

Google Sparse Hash The Google SparseHash project contains several hash-map implementations in use at Google, with different performance characteristics, including an implementation that optimizes for space and one that optimizes for speed. The memory-optimized one is extremely memory-efficient with only 2 bits/entry of overhead.
A number of language runtimes and/or standard libraries use hash tables to implement their support for associative arrays because of their efficiency. For some examples, see associative array#Language support.

External links

NIST entry on hash tables
Open addressing hash table removal algorithm from ICI programming language, ici_set_unassign in set.c (and other occurrences, with permission).
"good hash table primes". PlanetMath.
The Perl Wikibook - Perl Hash Variables

References

Donald Knuth. The Art of Computer Programming, Volume 3: Sorting and Searching, Third Edition. Addison-Wesley, 1997. ISBN 0-201-89685-0. Section 6.4: Hashing, pp.513–558.
Thomas H. Cormen, Charles E. Leiserson, Ronald L. Rivest, and Clifford Stein. Introduction to Algorithms, Second Edition. MIT Press and McGraw-Hill, 2001. ISBN 0262032937. Chapter 11: Hash Tables, pp.221–252.
Michael T. Goodrich and Roberto Tamassia. Data Structures and Algorithms in Java, 4th edition. John Wiley & Sons, Inc. ISBN: 0-471-73884-0. Chapter 9: Maps and Dictionaries. pp.369–418