Integrating sphere

An integrating sphere (also known as an Ulbricht sphere) is an optical component consisting of a hollow spherical cavity with its interior covered with a diffuse white reflective coating, with small holes for entrance and exit ports. Its relevant property is a uniform scattering or diffusing effect. Light rays incident on any point on the inner surface are, by multiple scattering reflections, distributed equally to all other points. The effects of the original direction of light are minimized. An integrating sphere may be thought of as a diffuser which preserves power but destroys spatial information. It is typically used with some light source and a detector for optical power measurement. A similar device is the focusing or Coblentz sphere, which differs in that it has a mirror-like (specular) inner surface rather than a diffuse inner surface.
In 1892, W. E. Sumpner published an expression for the throughput of a spherical enclosure with diffusely reflecting walls.[1] Ř. Ulbricht developed a practical realization of the integrating sphere, the topic of a publication in 1900.[2] It has become a standard instrument in photometry and radiometry and has the advantage over a goniophotometer that the total power produced by a source can be obtained in a single measurement. Other shapes, such as a cubical box, have also been theoretically analyzed.[3]
Even small commercial integrating spheres cost many thousands of dollars, as a result their use is often limited to industry and large academic institutions. However, 3D printing and homemade coatings have seen the production of experimentally accurate DIY spheres for very low cost.[4]
Theory
[edit]The theory of integrating spheres is based on these assumptions:
- Light hitting the sides of the sphere is scattered in a diffuse way i.e. Lambertian reflectance
- Only light that has been diffused in the sphere hits the ports or detectors used for probing the light
Using these assumptions the sphere multiplier can be calculated. This number is the average number of times a photon is scattered in the sphere, before it is absorbed in the coating or escapes through a port. This number increases with the reflectivity of the sphere coating and decreases with the ratio between the total area of ports and other absorbing objects and the sphere inner area. To get a high homogeneity a recommended sphere multiplier is 10-25.[5]
The theory further states that if the above criteria are fulfilled then the irradiance on any area element on the sphere will be proportional to the total radiant flux input to the sphere. Absolute measurements of instance luminous flux can then be done by measuring a known light source and determining the transfer function or calibration curve.
Total exit irradiance
[edit]For a sphere with radius r, reflection coefficient ρ, and source flux Φ, the initial reflected irradiance is equal to:
Every time the irradiance is reflected, the reflection coefficient exponentially grows. The resulting equation is
Since ρ ≤ 1, the geometric series converges and the total exit irradiance is:[6]
Applications
[edit]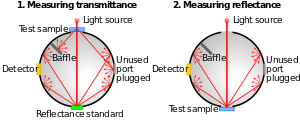
Integrating spheres are used for a variety of optical, photometric or radiometric measurements. They are used to measure the total light radiated in all directions from a lamp. An integrating sphere can be used to create a light source with apparent intensity uniform over all positions within its circular aperture, and independent of direction except for the cosine function inherent to ideally diffuse radiating surfaces (Lambertian surfaces). An integrating sphere can be used to measure the diffuse reflectance of surfaces, providing an average over all angles of illumination and observation.
A number of methods exist to measure the absolute reflectance of a test object mounted on an integrating sphere. In 1916, E. B. Rosa and A. H. Taylor published the first such method.[7] Subsequent work by A. H. Taylor,[8][9] Frank A. Benford,[10][11] C. H. Sharpe & W. F. Little,[12] Enoch Karrer,[13] and Leonard Hanssen & Simon Kaplan[14][15] expanded the number of unique methods which measure port-mounted test objects. Edwards et al.,[16] Korte & Schmidt,[17] and Van den Akker et al.[18] developed methods which measure center-mounted test objects.
Light scattered by the interior of the integrating sphere is evenly distributed over all angles. The integrating sphere is used in optical measurements. The total power (flux) of a light source can be measured without inaccuracy caused by the directional characteristics of the source, or the measurement device. Reflection and absorption of samples can be studied. The sphere creates a reference radiation source that can be used to provide a photometric standard.
Since all the light incident on the input port is collected, a detector connected to an integrating sphere can accurately measure the sum of all the ambient light incident on a small circular aperture. The total power of a laser beam can be measured, free from the effects of beam shape, incident direction, and incident position, as well as polarization.

Materials
[edit]The optical properties of the lining of the sphere greatly affect its accuracy. Different coatings must be used at visible, infrared and ultraviolet wavelengths. High-powered illumination sources may heat or damage the coating, so an integrating sphere will be rated for a maximum level of incident power. Various coating materials are used. For visible-spectrum light, early experimenters used a deposit of magnesium oxide, and barium sulfate also has a usefully flat reflectance over the visible spectrum. Various proprietary PTFE compounds are also used for visible light measurements. Finely-deposited gold is used for infrared measurements.
An important requirement for the coating material is the absence of fluorescence. Fluorescent materials absorb short-wavelength light and re-emit light at longer wavelengths. Due to the many scatterings this effect is much more pronounced in an integrating sphere than for materials irradiated normally.
Structure
[edit]The theory of the integrating sphere assumes a uniform inside surface with diffuse reflectivity approaching 100%. Openings where light can exit or enter, used for detectors and sources, are normally called ports. The total area of all ports must be small, less than about 5% of the surface area of the sphere, for the theoretical assumptions to be valid. Unused ports should therefore have matching plugs, with the interior surface of the plug coated with the same material as the rest of the sphere.
Integrating spheres vary in size from a few centimeters in diameter up to a few meters in diameter. Smaller spheres are typically used to diffuse incoming radiation, while larger spheres are used to measure integrating properties like the luminous flux of a lamp or luminaries which is then placed inside the sphere.
If the entering light is incoherent (rather than a laser beam), then it typically fills the source-port, and the ratio of source-port area to detector-port area is relevant.
Baffles are normally inserted in the sphere to block the direct path of light from a source-port to a detector-port, since this light will have non-uniform distribution.[19]
See also
[edit]
References
[edit]- ^ Sumpner, W. E. (1892). "The diffusion of light". Proceedings of the Physical Society of London. 12 (1): 10–29. Bibcode:1892PPSL...12...10S. doi:10.1088/1478-7814/12/1/304.
- ^ Ulbricht, Ř. (1900). "Die bestimmung der mittleren räumlichen lichtintensität durch nur eine messung". Electroteknische Zeit. (in German). 21: 595–610.
- ^ Sumpner, W. E. (1910). "The direct measurement of the total light emitted from a lamp". The Illuminating Engineer. 3: 323.
- ^ Tomes, John J.; Finlayson, Chris E. (2016). "Low cost 3D-printing used in an undergraduate project: an integrating sphere for measurement of photoluminescence quantum yield". European Journal of Physics. 37 (5): 055501. Bibcode:2016EJPh...37e5501T. doi:10.1088/0143-0807/37/5/055501. hdl:2160/43921. ISSN 0143-0807. S2CID 124621249. Retrieved 2021-10-12.
- ^ "Integrating Sphere Design and Applications" (PDF). SphereOptics. SphereOptics LLC. Archived from the original (PDF) on 2009-08-15.
- ^ Schott, John R. (2007). Remote Sensing: The Image Chain Approach. Oxford University Press. ISBN 978-0-19-972439-0. Retrieved 17 June 2020.
- ^ Rosa, E. B.; Taylor, A. H. (1916). "The integrating photometric sphere, its construction and use". Transactions of the Illumination Engineering Society. 11: 453.
- ^ Taylor, A. H. (1920). "The Measurement of Diffuse Reflection Factors and a New Absolute Reflectometer". Journal of the Optical Society of America. 4 (1): 9–23. doi:10.1364/JOSA.4.000009. hdl:2027/mdp.39015086549857. Retrieved 2021-10-12.
- ^ Taylor, A. H. (1935). "Errors in Reflectometry". Journal of the Optical Society of America. 25 (2): 51–56. doi:10.1364/JOSA.25.000051. Retrieved 2021-10-12.
- ^ Benford, Frank A. (1920). "An absolute method for determining coefficients of diffuse reflection". General Electric Review. 23: 72–75.
- ^ Benford, Frank A. (1934). "A Reflectometer for All Types of Surfaces". Journal of the Optical Society of America. 24 (7): 165–174. doi:10.1364/JOSA.24.000165. Retrieved 2021-10-12.
- ^ Sharpe, C. H.; Little, W. F. (1920). "Measurements of Reflectance Factors". Transactions of the Illumination Engineering Society. 15: 802.
- ^ Karrer, Enoch (1921). "Use of the Ulbricht Sphere in measuring reflection and transmission factors". Scientific Papers of the Bureau of Standards. 17: 203–225. doi:10.6028/nbsscipaper.092. Retrieved 2021-10-12.
- ^ Hanssen, Leonard; Kaplan, Simon (1999-02-02). "Infrared diffuse reflectance instrumentation and standards at NIST". Analytica Chimica Acta. 380 (2–3): 289–302. Bibcode:1999AcAC..380..289H. doi:10.1016/S0003-2670(98)00669-2. Retrieved 2021-10-12.
- ^ Hanssen, Leonard (2001-07-01). "Integrating-sphere system and method for absolute measurement of transmittance, reflectance, and absorptance of specular samples". Applied Optics. 40 (19): 3196–3204. Bibcode:2001ApOpt..40.3196H. doi:10.1364/AO.40.003196. PMID 11958259. Retrieved 2021-10-12.
- ^ Edwards, D. K.; Gier, J. T.; Nelson, K. E.; Roddick, R. D. (1961). "Integrating Sphere for Imperfectly Diffuse Samples". Journal of the Optical Society of America. 51 (11): 1279–1288. doi:10.1364/JOSA.51.001279. Retrieved 2021-10-12.
- ^ Korte, H.; Schmidt, M. (1967). "Über Messungen des Leuchtdichtefaktors an beliebig reflektierenden Proben". Lichttechnik (in German). 19: 135A–137A.
- ^ Van den Akker, J. A.; Dearth, Leonard R.; Shillcox, Wayne M. (1966). "Evaluation of Absolute Reflectance for Standardization Purposes". Journal of the Optical Society of America. 56 (2): 250–252. doi:10.1364/JOSA.56.000250. Retrieved 2021-10-12.
- ^ Hanssen, Leonard M.; Prokhorov, Alexander V.; Khromchenko, Vladimir B. (2003-11-14). Specular baffle for improved infrared integrating sphere performance. Optical Science and Technology, SPIE's 48th Annual Meeting. Vol. 5192. San Diego, California, United States: SPIE. doi:10.1117/12.508299. Retrieved 2021-10-12.
External links
[edit]- RP Photonics, Encyclopedia of Laser Physics and Technology, Integrating spheres
- Pike Technologies, Integrating Spheres – Introduction and Theory, Pike Technologies Application Note
- Newport, Flange Mount Integrating Spheres
- Whitehead, Lorne A.; Mossman, Michele A. (2006). "Jack O'Lanterns and integrating spheres: Halloween Physics". American Journal of Physics. 74 (6): 537–541. Bibcode:2006AmJPh..74..537W. doi:10.1119/1.2190687.
- Ducharme, Alfred; Daniels, Arnold; Grann, Eric; Boreman, Glenn (1997). "Design of an Integrating Sphere as a Uniform Illumination Source". IEEE Transactions on Education. 40 (2): 131–134. Bibcode:1997ITEdu..40..131D. doi:10.1109/13.572326. S2CID 61946451.
- Peter Hiscocks, Integrating Sphere for Luminance Calibration Archived 2012-01-06 at the Wayback Machine, Rev 6, May 2016
- Ci Systems, Integrating sphere introduction, mechanical structure, calibration and sources
- Electro-Optical Industries, Integrating Spheres
- The Status of Integrating Sphere in China



