Barometric formula
The barometric formula is a formula used to model how the pressure (or density) of the air changes with altitude.
Pressure equations
[edit]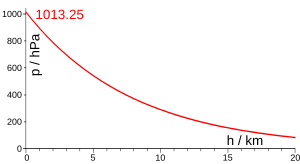
There are two equations for computing pressure as a function of height. The first equation is applicable to the atmospheric layers in which the temperature is assumed to vary with altitude at a non null lapse rate of : The second equation is applicable to the atmospheric layers in which the temperature is assumed not to vary[citation needed] with altitude (lapse rate is null): where:
- = reference pressure
- = reference temperature (K)
- = temperature lapse rate (K/m) in ISA
- = geopotential height at which pressure is calculated (m)
- = geopotential height of reference level b (meters; e.g., hb = 11 000 m)
- = universal gas constant: 8.3144598 J/(mol·K)
- = gravitational acceleration: 9.80665 m/s2
- = molar mass of Earth's air: 0.0289644 kg/mol
Or converted to imperial units:[1]
- = reference pressure
- = reference temperature (K)
- = temperature lapse rate (K/ft) in ISA
- = height at which pressure is calculated (ft)
- = height of reference level b (feet; e.g., hb = 36,089 ft)
- = universal gas constant; using feet, kelvins, and (SI) moles: 8.9494596×104 lb·ft2/(lb-mol·K·s2)
- = gravitational acceleration: 32.17405 ft/s2
- = molar mass of Earth's air: 28.9644 lb/lb-mol
The value of subscript b ranges from 0 to 6 in accordance with each of seven successive layers of the atmosphere shown in the table below. In these equations, g0, M and R* are each single-valued constants, while P, L, T, and h are multivalued constants in accordance with the table below. The values used for M, g0, and R* are in accordance with the U.S. Standard Atmosphere, 1976, and the value for R* in particular does not agree with standard values for this constant.[2] The reference value for Pb for b = 0 is the defined sea level value, P0 = 101 325 Pa or 29.92126 inHg. Values of Pb of b = 1 through b = 6 are obtained from the application of the appropriate member of the pair equations 1 and 2 for the case when h = hb+1.[2]
| Subscript b | Geopotential
height above MSL (h) |
Static pressure | Standard temperature (K) |
Temperature lapse rate | Exponent g0 M / R L | |||
|---|---|---|---|---|---|---|---|---|
| (m) | (ft) | (Pa) | (inHg) | (K/m) | (K/ft) | |||
| 0 | 0 | 0 | 101 325.00 | 29.92126 | 288.15 | 0.0065 | 0.0019812 | 5.25588 |
| 1 | 11 000 | 36,089 | 22 632.10 | 6.683245 | 216.65 | 0.0 | 0.0 | — |
| 2 | 20 000 | 65,617 | 5474.89 | 1.616734 | 216.65 | -0.001 | -0.0003048 | -34.1626 |
| 3 | 32 000 | 104,987 | 868.02 | 0.2563258 | 228.65 | -0.0028 | -0.00085344 | -12.2009 |
| 4 | 47 000 | 154,199 | 110.91 | 0.0327506 | 270.65 | 0.0 | 0.0 | — |
| 5 | 51 000 | 167,323 | 66.94 | 0.01976704 | 270.65 | 0.0028 | 0.00085344 | 12.2009 |
| 6 | 71 000 | 232,940 | 3.96 | 0.00116833 | 214.65 | 0.002 | 0.0006096 | 17.0813 |
Density equations
[edit]The expressions for calculating density are nearly identical to calculating pressure. The only difference is the exponent in Equation 1.
There are two equations for computing density as a function of height. The first equation is applicable to the standard model of the troposphere in which the temperature is assumed to vary with altitude at a lapse rate of ; the second equation is applicable to the standard model of the stratosphere in which the temperature is assumed not to vary with altitude.
Equation 1:
which is equivalent to the ratio of the relative pressure and temperature changes
Equation 2:
where
- = mass density (kg/m3)
- = standard temperature (K)
- = standard temperature lapse rate (see table below) (K/m) in ISA
- = height above sea level (geopotential meters)
- = universal gas constant 8.3144598 N·m/(mol·K)
- = gravitational acceleration: 9.80665 m/s2
- = molar mass of Earth's air: 0.0289644 kg/mol
or, converted to U.S. gravitational foot-pound-second units (no longer used in U.K.):[1]
- = mass density (slug/ft3)
- = standard temperature (K)
- = standard temperature lapse rate (K/ft)
- = height above sea level (geopotential feet)
- = universal gas constant: 8.9494596×104 ft2/(s·K)
- = gravitational acceleration: 32.17405 ft/s2
- = molar mass of Earth's air: 0.0289644 kg/mol
The value of subscript b ranges from 0 to 6 in accordance with each of seven successive layers of the atmosphere shown in the table below. The reference value for ρb for b = 0 is the defined sea level value, ρ0 = 1.2250 kg/m3 or 0.0023768908 slug/ft3. Values of ρb of b = 1 through b = 6 are obtained from the application of the appropriate member of the pair equations 1 and 2 for the case when h = hb+1.[2]
In these equations, g0, M and R* are each single-valued constants, while ρ, L, T and h are multi-valued constants in accordance with the table below. The values used for M, g0 and R* are in accordance with the U.S. Standard Atmosphere, 1976, and that the value for R* in particular does not agree with standard values for this constant.[2]
| Subscript b | Geopotential
height above MSL (h) |
Mass Density () | Standard Temperature (T') (K) |
Temperature Lapse Rate (L) | |||
|---|---|---|---|---|---|---|---|
| (m) | (ft) | (kg/m3) | (slug/ft3) | (K/m) | (K/ft) | ||
| 0 | 0 | 0 | 1.2250 | 2.3768908×10−3 | 288.15 | 0.0065 | 0.0019812 |
| 1 | 11 000 | 36,089.24 | 0.36391 | 7.0611703×10−4 | 216.65 | 0.0 | 0.0 |
| 2 | 20 000 | 65,616.79 | 0.08803 | 1.7081572×10−4 | 216.65 | -0.001 | -0.0003048 |
| 3 | 32 000 | 104,986.87 | 0.01322 | 2.5660735×10−5 | 228.65 | -0.0028 | -0.00085344 |
| 4 | 47 000 | 154,199.48 | 0.00143 | 2.7698702×10−6 | 270.65 | 0.0 | 0.0 |
| 5 | 51 000 | 167,322.83 | 0.00086 | 1.6717895×10−6 | 270.65 | 0.0028 | 0.00085344 |
| 6 | 71 000 | 232,939.63 | 0.000064 | 1.2458989×10−7 | 214.65 | 0.002 | 0.0006096 |
Derivation
[edit]The barometric formula can be derived using the ideal gas law:
Assuming that all pressure is hydrostatic: and dividing this equation by we get:
Integrating this expression from the surface to the altitude z we get:
Assuming linear temperature change and constant molar mass and gravitational acceleration, we get the first barometric formula:
Instead, assuming constant temperature, integrating gives the second barometric formula:
In this formulation, R* is the gas constant, and the term R*T/Mg gives the scale height (approximately equal to 8.4 km for the troposphere).
(For exact results, it should be remembered that atmospheres containing water do not behave as an ideal gas. See real gas or perfect gas or gas for further understanding.)
See also
[edit]References
[edit]- ^ a b Mechtly, E. A., 1973: The International System of Units, Physical Constants and Conversion Factors. NASA SP-7012, Second Revision, National Aeronautics and Space Administration, Washington, D.C.
- ^ a b c d U.S. Standard Atmosphere, 1976, U.S. Government Printing Office, Washington, D.C., 1976. (Linked file is 17 Mb)


![{\displaystyle P=P_{b}\left[1-{\frac {L_{M,b}}{T_{M,b}}}(h-h_{b})\right]^{\frac {g_{0}'M_{0}}{R^{*}L_{M,b}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f25dabf8a48739c7172a85219680d1292beaacea)
![{\displaystyle P=P_{b}\exp \left[{\frac {-g_{0}M\left(h-h_{b}\right)}{R^{*}{T_{M,b}}}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/79ca5398673c542ef11a047b135a8b3599d1e56b)








![{\displaystyle \rho =\rho _{b}\left[{\frac {T_{b}-(h-h_{b})L_{b}}{T_{b}}}\right]^{\left({\frac {g_{0}M}{R^{*}L_{b}}}-1\right)}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f5d6a42b1448ee9b7f539d10a2f8593df1b769d5)

![{\displaystyle \rho =\rho _{b}\exp \left[{\frac {-g_{0}M\left(h-h_{b}\right)}{R^{*}T_{b}}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/37d5367beea036fb4f0423a2949a1d08f835fb7c)
















![{\displaystyle P=P_{0}\cdot \left[{\frac {T}{T_{0}}}\right]^{\textstyle {\frac {Mg}{R^{*}L}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/18247095fe5ee08cbd5d33dee816eb6a288eb9c7)
