Lamination (topology)
Appearance

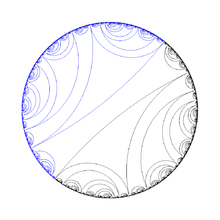
In topology, a branch of mathematics, a lamination is a :
- "topological space partitioned into subsets"[1]
- decoration (a structure or property at a point) of a manifold in which some subset of the manifold is partitioned into sheets of some lower dimension, and the sheets are locally parallel.
A lamination of a surface is a partition of a closed subset of the surface into smooth curves.
It may or may not be possible to fill the gaps in a lamination to make a foliation.[2]
Examples
[edit]
- A geodesic lamination of a 2-dimensional hyperbolic manifold is a closed subset together with a foliation of this closed subset by geodesics.[3] These are used in Thurston's classification of elements of the mapping class group and in his theory of earthquake maps.
- Quadratic laminations, which remain invariant under the angle doubling map.[4] These laminations are associated with quadratic maps.[5][6] It is a closed collection of chords in the unit disc.[7] It is also topological model of Mandelbrot or Julia set.
See also
[edit]Notes
[edit]- ^ "Lamination", Encyclopedia of Mathematics, EMS Press, 2001 [1994]
- ^ "Defs.txt". Archived from the original on 2009-07-13. Retrieved 2009-07-13. Oak Ridge National Laboratory
- ^ Laminations and foliations in dynamics, geometry and topology: proceedings of the conference on laminations and foliations in dynamics, geometry and topology, May 18-24, 1998, SUNY at Stony Brook
- ^ Houghton, Jeffrey. "Useful Tools in the Study of Laminations" Paper presented at the annual meeting of the Mathematical Association of America MathFest, Omni William Penn, Pittsburgh, PA, Aug 05, 2010
- ^ Tomoki KAWAHIRA: Topology of Lyubich-Minsky's laminations for quadratic maps: deformation and rigidity (3 heures)
- ^ Topological models for some quadratic rational maps by Vladlen Timorin
- ^ Modeling Julia Sets with Laminations: An Alternative Definition by Debra Mimbs Archived 2011-07-07 at the Wayback Machine
