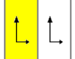List of planar symmetry groups

This article summarizes the classes of discrete planar symmetry groups. The symmetry groups are named here by three naming schemes: International notation, orbifold notation, and Coxeter notation.

There are three kinds of symmetry groups of the plane:

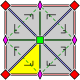
Rosette groups

There are two families of discrete two-dimensional point groups, and they are specified with parameter n, which is the order of the group of the rotations in the group.

Family	Intl (orbifold)	Geo ^[1] Coxeter	Schönflies	Order	Examples
Cyclic symmetry	n (n•)	n [n]⁺	C_n	n	[ ]⁺	[2]⁺ ^(*)	[3]⁺	[4]⁺	[5]⁺	File:Crop circles Swirl.jpg [6]⁺
Dihedral symmetry	nm (*n•)	n [n]	D_n	2n	[ ]	[2]	[3]	[4]	[5]	[6]
Dihedral symmetry	nm (*n•)	n [n]	D_n	2n	(*) The Yin and Yang symbol has 2-fold cyclic symmetry of geometry but inverted colors.

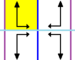
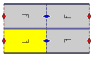
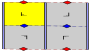
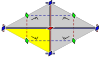
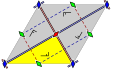
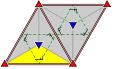
Frieze groups

The 7 frieze groups, the two-dimensional line groups, with a direction of periodicity are given with five notational names. The Schönflies notation is given as infinite limits of 7 dihedral groups. The yellow regions represent the infinite fundamental domain in each.

[∞],
IUC (Orbifold)	Geo	Schönflies	Coxeter	Fundamental domain	Example
p1 (∞•)	p1	C_∞	[∞]⁺
p1m1 (*∞•)	p1	C_∞v	[∞]

[2,∞⁺],
IUC (Orbifold)	Geo	Schönflies	Coxeter	Fundamental domain	Example
p11g (∞×)	p._g1	S_2∞	[2⁺,∞⁺]
p11m (∞*)	p. 1	C_∞h	[2,∞⁺]

[2,∞],
IUC (Orbifold)	Geo	Schönflies	Coxeter
p2 (22∞)	p2	D_∞	[2,∞]⁺
p2mg (2*∞)	p2_g	D_∞d	[2⁺,∞]
p2mm (*22∞)	p2	D_∞h	[2,∞]

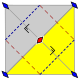
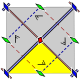
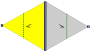
Wallpaper groups

The 17 wallpaper groups, with finite fundamental domains, are given by International notation, orbifold notation, and Coxeter notation, classified by the 5 Bravais lattices in the plane: square, oblique (parallelogrammatic), hexagonal (60 degree rhombic), rectangular, and centered rectangular (rhombic).

The p1 and p2 groups, with no reflectional symmetry, are repeated in all classes. The related pure reflectional Coxeter group are given with all classes except oblique.

Square
[4,4],
IUC (Orbifold) Geometric	Coxeter	Fundamental domain
p1 (°) p1	[∞⁺,2,∞⁺]
p2 (2222) p2	[(4,1⁺,4,2⁺)] [1⁺,4,1⁺,4,1⁺]
pgg (22×) p_g2_g	[4⁺,4⁺]
pmm (*2222) p2	[4,1⁺,4] [1⁺,4,4,1⁺]
cmm (2*22) c2	[[4⁺,4⁺]] [(4,4,2⁺)]
p4 (442) p4	[4,4]⁺
p4g (4*2) p_g4	[4⁺,4]
p4m (*442) p4	[4,4]

Parallelogrammatic (oblique)
p1 (°) p1	[∞⁺,2,∞⁺]
p2 (2222) p2	[∞,2,∞]⁺

Rectangular
[∞_h,2,∞_v],
IUC (Orbifold) Geometric	Coxeter	Fundamental domain
p1 (°) p1	[∞⁺,2,∞⁺]
p2 (2222) p2	[∞,2,∞]⁺
pgg (22×) p_g2_g	[[∞,2,∞]⁺]
pg(h) (××) p_g1	h: [∞⁺,(2,∞)⁺]
pg(v) (××) p_g1	v: [(∞,2)⁺,∞⁺]
pgm (22*) p_g2	h: [(∞,2)⁺,∞]
pmg (22*) p_g2	v: [∞,(2,∞)⁺]
pm(h) (**) p1	h: [∞⁺,2,∞]
pm(v) (**) p1	v: [∞,2,∞⁺]
pmm (*2222) p2	[∞,2,∞]

Rhombic
[∞_h,2⁺,∞_v],
p1 (°) p1	[∞⁺,2,∞⁺]
p2 (2222) p2	[∞⁺,2⁺,∞⁺]⁺ [(∞⁺,2⁺,∞⁺,2⁺)]
cm(h) (*×) c1	h: [∞⁺,2⁺,∞]
cm(v) (*×) c1	v: [∞,2⁺,∞⁺]
pgg (22×) p_g2_g	[∞⁺,2⁺,∞⁺]
cmm (2*22) c2	[∞,2⁺,∞]

Hexagonal/Triangular
[6,3], / [3^[3]],
IUC (Orbifold) Geometric	Coxeter	Fundamental domain
p1 (°) p1	[∞⁺,2,∞⁺]
p2 (2222) p2	[∞,2,∞]⁺
cmm (2*22) c2	[∞,2⁺,∞]
p3 (333) p3	[1⁺,6,3⁺] [3^[3]]⁺
p3m1 (*333) p3	[1⁺,6,3] [3^[3]]
p31m (3*3) h3	[6,3⁺] [3⁺[3^[3]]]
p6 (632) p6	[6,3]⁺ [3[3^[3]]]⁺
p6m (*632) p6	[6,3] [3[3^[3]]]

Notes

^ The Crystallographic Space groups in Geometric algebra, D. Hestenes and J. Holt, Journal of Mathematical Physics. 48, 023514 (2007) (22 pages) PDF [1]

References

The Symmetries of Things 2008, John H. Conway, Heidi Burgiel, Chaim Goodman-Strass, ISBN 978-1-56881-220-5
On Quaternions and Octonions, 2003, John Horton Conway and Derek A. Smith ISBN 978-1-56881-134-5
Kaleidoscopes: Selected Writings of H.S.M. Coxeter, editied by F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss, Wiley-Interscience Publication, 1995, ISBN 978-0-471-01003-6 [2]
- (Paper 22) H.S.M. Coxeter, Regular and Semi Regular Polytopes I, [Math. Zeit. 46 (1940) 380–407, MR 2,10]
- (Paper 23) H.S.M. Coxeter, Regular and Semi-Regular Polytopes II, [Math. Zeit. 188 (1985) 559–591]
- (Paper 24) H.S.M. Coxeter, Regular and Semi-Regular Polytopes III, [Math. Zeit. 200 (1988) 3–45]
N.W. Johnson: Geometries and Transformations, Manuscript, (2011) Chapter 11: Finite symmetry groups

External links

"Conway's manuscript" on Orbifold notation (Notation changed from this original, x is now used in place of open-dot, and o is used in place of the closed dot)
The 17 Wallpaper Groups

[1] The Crystallographic Space groups in Geometric algebra, D. Hestenes and J. Holt, Journal of Mathematical Physics. 48, 023514 (2007) (22 pages) PDF [1]

[1]