Measurement of a Circle

Measurement of a Circle (Greek: Κύκλου μέτρησις, Kuklou metrēsis) is a treatise that consists of three propositions by Archimedes. The treatise is only a fraction of what was a longer work.

Propositions

Proposition one

The circle and the triangle are equal in area.

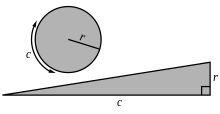
Proposition one states:

The area of any circle is equal to a right-angled triangle in which one of the sides about the right angle is equal to the radius, and the other to the circumference, of the circle.

Any circle with a circumference c and a radius r is equal in area with a right triangle with the two legs being c and r. This proposition is proved by the method of exhaustion.

Proposition two

Proposition two states:

The area of a circle is to the square on its diameter as 11 to 14.

This proposition could not have been placed by Archimedes, for it relies on the outcome of the third proposition.

Proposition three

Examples of how Archimedes calculated pi. Archimedes used a 96-sided polygon to find his estimate.

Proposition three states:

The ratio of the circumference of any circle to its diameter is less than $3{\tfrac {10}{70}}$ but greater than $3{\tfrac {10}{71}}$.

This approximates the mathematical constant π. He found the upper and lower limits to the value of π by inscribing and circumscribing a circle with two similar 96-sided regular polygons.

Approximation to square roots

This proposition also contains accurate approximations to the square root of 3 (one larger and one smaller) and other larger non-perfect square roots; however, Archimedes gives no explanation as to how he found these numbers. He gives the upper and lower bounds to √3 as  ${\tfrac {1351}{780}}>{\sqrt {3}}>{\tfrac {265}{153}}\,.$