Morin surface

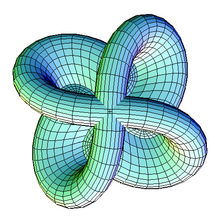
The Morin surface is the half-way model of the sphere eversion discovered by Bernard Morin. It features fourfold rotational symmetry.

If the original sphere to be everted has its outer surface colored green and its inner surface colored red, then when the sphere is transformed through homotopy into a Morin surface, half of the outwardly visible Morin surface will be green, and half red:

Half of a Morin surface corresponds to the exterior (green) of the sphere
to which it is homeomorphic, and the other symmetric half to the interior (red).

Then, rotating the surface 90° around its axis of symmetry will exchange its colors, i.e. will exchange the inner-outer polarity of the orientable surface, so that retracing the steps of the homotopy at exactly the same position back to the original sphere after having so rotated the Morin surface will yield a sphere whose outer surface is red and whose inner surface is green: a sphere which has been turned inside out. The following is a summary of the eversion:

1. sphere: green outside, red inside...
2. transforms into...
3. Morin surface,
3'. Morin surface rotated 90°...
2'. inversely transforms into...
1'. sphere: red outside, green inside.

Structure of the Morin surface

The Morin surface can be separated into four congruent quarter sections. These sections may be here called section East, section South, section West, and section North, or — respectively — section 0, section 1, section 2, and section 3.

Section East of the Morin surface.

The Morin surface has a quadruple point through which passes its axis of symmetry. This quadruple point is the starting point and the end point of six lines of double points. Each of the quarter sections is bounded by three of these lines of double points, so that each quarter section is homeomorphic to a triangle. Section East is now shown schematically:

The diagram shows section East bounded by three loops: ABCDA, AEFGA, and AHIJA. The third loop, AHIJA, is a line of double points where section East intersects with itself. Loop ABCDA is only a line of double points when section East is joined to section West, and loop AEFGA is only a line of double points when section East is joined to section South. Point is the quadruple point which is actually the overlapping of four different points: A₀, A₁, A₂, A₃.

This is how section East is joined to the other sections: let each of its bounding loops be specified by an ordered quintuple of points, then

(A_{1},B,C,D,A_{3})=(A_{1},D'',C'',B'',A_{3})

(A_{2},E,F,G,A_{3})=(A_{2},H',I',J',A_{3})

(A_{1},H,I,J,A_{2})=(A_{1},E''',F''',G''',A_{2})

where unprimed points belong to section 0 (East), primed points belong to section 1 (South), double-primed points belong to section 2 (West), and triple-primed points belong to section 3 (North).

The remaining three loops connect sections as follows:

(A_{2},B',C',D',A_{0})=(A_{2},D''',C''',B''',A_{0})

(A_{3},E',F',G',A_{0})=(A_{3},H'',I'',J'',A_{0})

(A_{0},E'',F'',G'',A_{1})=(A_{0},H''',I''',J''',A_{1}).

Section East has, considered just by itself, one loop of double points: AHIJA. If the surface is unwound and flattened the result will be the following:

which is homeomorphic to a triangle:

Joining the four triangular sections at their seams will produce a tetrahedron:

which is homeomorphic to a sphere, which shows the Morin surface is a self-intersecting sphere.