Octadecahedron
In geometry, an octadecahedron (or octakaidecahedron) is a polyhedron with 18 faces. No octadecahedron is regular; hence, the name does not commonly refer to one specific polyhedron.
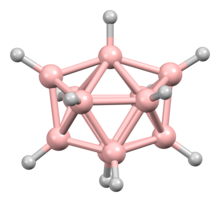
In chemistry, "the octadecahedron" commonly refers to a specific structure with C2v symmetry, the edge-contracted icosahedron, formed from a regular icosahedron with one edge contracted. It is the shape of the closo-boranate ion [B11H11]2−.
Convex[edit]
There are 107,854,282,197,058 topologically distinct convex octadecahedra, excluding mirror images, having at least 11 vertices.[2] (Two polyhedra are "topologically distinct" if they have intrinsically different arrangements of faces and vertices, such that it is impossible to distort one into the other simply by changing the lengths of edges or the angles between edges or faces.)
Examples[edit]
The most familiar octadecahedra are the heptadecagonal pyramid, hexadecagonal prism, and the octagonal antiprism. The hexadecagonal prism and the octagonal antiprism are uniform polyhedra, with regular bases and square or equilateral triangular sides. Four more octadecahedra are also found among the Johnson solids: the square gyrobicupola, the square orthobicupola, the elongated square cupola (also known as the diminished rhombicuboctahedron), and the sphenomegacorona. Four Johnson solids have octadecahedral duals: the elongated triangular orthobicupola, the elongated triangular gyrobicupola, the gyroelongated triangular bicupola, and the triangular hebesphenorotunda.
 Octagonal antiprism |
 Square gyrobicupola |
 Sphenomegacorona |
 Elongated hexagonal bipyramid |
In addition, some uniform star polyhedra are also octadecahedra:
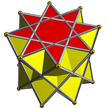 Octagrammic antiprism |
 Octagrammic crossed-antiprism |
 Small rhombihexahedron |
 Small dodecahemidodecahedron |
 Great rhombihexahedron |
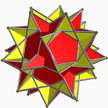 Great dodecahemidodecahedron |
References[edit]
- ^ O. Volkov; W. Dirk; U. Englert; P. Paetzold (1999). "Undecaborates M2[B11H11]: Facile Synthesis, Crystal Structure, and Reactions". Z. Anorg. Allg. Chem. 625 (7): 1193–1200. doi:10.1002/(SICI)1521-3749(199907)625:7<1193::AID-ZAAC1193>3.0.CO;2-L.
- ^ Counting polyhedra
