PH-tree
| PH-tree | ||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Type | tree, map | |||||||||||||||||||||||
| Invented | 2014 | |||||||||||||||||||||||
| ||||||||||||||||||||||||
The PH-tree[1] is a tree data structure used for spatial indexing of multi-dimensional data (keys) such as geographical coordinates, points, feature vectors, rectangles or bounding boxes. The PH-tree is space partitioning index[2] with a structure similar to that of a quadtree or octree.[3] However, unlike quadtrees, it uses a splitting policy based on tries and similar to Crit bit trees that is based on the bit-representation of the keys. The bit-based splitting policy, when combined with the use of different internal representations for nodes, provides scalability with high-dimensional data. The bit-representation splitting policy also imposes a maximum depth, thus avoiding degenerated trees and the need for rebalancing.[1]
Overview
[edit]The basic PH-tree is a spatial index that maps keys, which are d-dimensional vectors with integers, to user defined values. The PH-tree is a multi-dimensional generalization of a Crit bit tree in the sense that a Crit bit tree is equivalent to a PH-tree with -dimensional keys. Like the Crit bit tree, and unlike most other spatial indexes, the PH-tree is a map rather than a multimap.[1][4]
A d-dimensional PH-tree is a tree of nodes where each node partitions space by subdividing it into quadrants (see below for how potentially large nodes scales with high dimensional data). Each quadrant contains at most one entry, either a key-value pair (leaf quadrant) or a key-subnode pair. For a key-subnode pair, the key represents the center of the subnode. The key is also the common prefix (bit-representation) of all keys in the subnode and its child subnodes. Each node has at least two entries, otherwise it is merged with the parent node.[1]
Some other structural properties of PH-trees are:[1]
- They are -ary trees.
- They are inherently unbalanced but imbalance is limited due to their depth being limited to the bit width of the keys, e.g. to 32 for a -dimensional key with 32bit integers.
- Insertion or removal operations cause exactly one node to be modified and potentially a second node to be added or removed. This can be useful for concurrent implementations. This also means little variation in modification cost.
- Their structure is independent from insertion/removal order.
Splitting strategy
[edit]Similar to most quadtrees, the PH-tree is a hierarchy of nodes where every node splits the space in all d dimensions.[1] Thus, a node can have up to subnodes, one for each quadrant.

Quadrant numbering
[edit]The PH-tree uses the bits of the multi-dimensional keys to determine their position in the tree. All keys that have the same leading bits are stored in the same branch of the tree.[1]
For example, in a node at level L, to determine the quadrant where a key should be inserted (or removed or looked up), it looks at the L's bit of each dimension of the key. For a 3D node with 8 quadrants (forming a cube) the L's bit of the first dimension of the key determines whether the target quadrant is on the left or the right of the cube, the L's bit of the second dimension determines whether it is at the front or the back, and the L's bit of the third dimension determines bottom vs top, see picture.

1D example
[edit]Example with three 1D keys with 8bit values: , and . Adding and to an empty tree results in a single node. The two keys first differ in their 6th bit so the node has a level (starting with 0). The node has a 5bit prefix representing the common 5 bits of both keys. The node has two quadrants, each key is stored in one quadrant. Adding a third key results in one additional node at with one quadrant containing the original node as subnode and the other quadrant containing the new key .[citation needed]
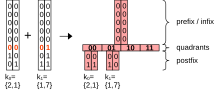
2D example
[edit]With 2D keys every node has quadrants. The position of the quadrant where a key is stored is extracted from the respective bits of the keys, one bit from each dimension. The four quadrants of the node form a 2D hypercube (quadrants may be empty). The bits that are extracted from the keys form the hypercube address , for and for . is effectively the position of the quadrant in the node's hypercube.[citation needed]
Node structure
[edit]The ordering of the entries in a node always follows Z-ordering. Entries in a node can, for example, be stored in fixed size arrays of size . h is then effectively the array index of a quadrant. This allows lookup, insert and remove with and there is no need to store h. Space complexity is however per node, so it is less suitable for high dimensional data.[1]
Another solution is to store entries in a sorted collection, such as dynamic arrays and/or B-trees. This slows down lookup operations to but reduces memory consumption to .[1]
The original implementation aimed for minimal memory consumption by switching between fixed and dynamic array representation depending on which uses less memory.[1] Other implementations [1][2] do not switch dynamically but use fixed arrays for , dynamic arrays for and B-trees for high dimensional data.
Operations
[edit]Lookup, insertion and removal operations all work very similar: find the correct node, then perform the operation on the node. Window queries and k-nearest-neighbor searches are more complex.
Lookup
[edit]The Lookup operation determines whether a key exists in the tree. It walks down the tree and checks every node whether it contains a candidate subnode or a user value that matches the key.[1]
function lookup(key) is
entry ← get_root_entry() // if the tree is not empty the root entry contains a root node
while entry != NIL && entry.is_subnode() do
node ← entry.get_node()
entry ← node.get_entry(key)
repeat
return entry // entry can be NIL
function get_entry(key) is
node ← current node
h ← extract_bits_at_depth(key, node.get_depth()}
entry ← node.get_entry_at(h)
return entry // entry can be NIL
Insert
[edit]The Insert operation inserts a new key-value pair into the tree unless they key already exists. The operation traverses the tree like the Lookup function and then inserts the key into the node. There are several cases to consider:[1]
- The quadrant is empty and we can simply insert a new entry into the quadrant and return.
- The quadrant contains a user entry with a key that is identical to the new entry. One way to deal with such a collision is to return a flag that indicates failed insertion. If the tree is implemented as multi-map with a collection as the node's entry, the new value is added to that collection.
- The quadrant contains an entry (user entry or subnode entry) with a different key. This case requires replacing the existing entry with a new subnode that holds the old and the new entry.
function insert(node, key, value)
level ← node.get_level() // Level is 0 for root
h ← extract_bits_at_level(key, level)
entry ← node.get_entry(h)
if entry == NIL then
// Case 1.
entry_new ← create_entry(key, value)
node.set_entry(h, entry_new)
else if !entry.is_subnode() && entry.get_key() == key then
// Case 2. Collision, there is already an entry
return ← failed_insertion
else
// Case 3.
level_diff ← get_level_of_difference(key, entry.get_key())
entry_new ← create_entry(key, value)
// new subnode with existing entry and new entry
subnode_new ← create_node(level_diff, entry, entry_new)
node.set_entry(h, subnode_new)
end if
return
Remove
[edit]Removal works inversely to insertion, with the additional constraint that any subnode has to be removed if less than two entries remain. The remaining entry is moved to the parent node.[1]
Window queries
[edit]Window queries are queries that return all keys that lie inside a rectangular axis-aligned hyperbox. They can be defined to be two d-dimensional points and that represent the "lower left" and "upper right" corners of the query box. A trivial implementation traverses all entries in a node (starting with the root node) and if an entry matches it either adds it to the result list (if it is a user entry) or recursively traverses it (if it is a subnode).[1]
function query(node, min, max, result_list) is
foreach entry ← node.get_entries() do
if entry.is_subnode() then
if entry.get_prefix() >= min and entry.get_prefix() <= max then
query(entry.get_subnode(), min, max, result_list)
end if
else
if entry.get_key() >= min and entry.get_key() <= max then
result_list.add(entry)
end if
end if
repeat
return
In order to accurately estimate query time complexity the analysis needs to include the dimensionality . Traversing and comparing all entries in a node has a time complexity of because each comparison of -dimensional key with takes time. Since nodes can have up to entries, this does not scale well with increasing dimensionality . There are various ways how this approach can be improved by making use of the hypercube address h.[4]
Min h & max h
[edit]The idea is to find minimum and maximum values for the quadrant's addresses such that the search can avoid some quadrants that do not overlap with the query box. Let be the center of a node (this is equal to the node's prefix) and and be two bit strings with bits each. Also, let subscript with indicate the 's bit of and and the 'th dimension of , and .
Let and . then has a `` for every dimension where the "lower" half of the node and all quadrants in it does not overlap with the query box. Similarly, has a `` for every dimension where the "upper" half does not overlap with the query box.
and then present the lowest and highest in a node that need to be traversed. Quadrants with or do not intersect with the query box. A proof is available in.[4] With this, the above query function can be improved to:
function query(node, min, max, result_list) is
h_min ← calculate h_min
h_max ← calculate h_max
for each entry ← node.get_entries_range(h_min, h_max) do
[ ... ]
repeat
return
Calculating and is . Depending on the distribution of the occupied quadrants in a node this approach will allow avoiding anywhere from no to almost all key comparisons. This reduces the average traversal time but the resulting complexity is still .[4]
Check quadrants for overlap with query box
[edit]Between and there can still be quadrants that do not overlap with the query box. Idea: and each have one bit for every dimensions that indicates whether the query box overlaps with the lower/upper half of a node in that dimension. This can be used to quickly check whether a quadrant overlaps with the query box without having to compare -dimensional keys: a quadrant overlaps with the query box if for every `` bit in there is a corresponding `` bit in and for every `` bit in there is a corresponding `` bit in . On a CPU with 64bit registers it is thus possible to check for overlap of up to -dimensional keys in .[4]
function is_overlap(h, h_min, h_max) is return (h | h_min) & h_max == h // evaluates to 'true' if quadrant and query overlap.
function query(node, min, max, result_list) is
h_min ← calculate h_min
h_max ← calculate h_max
for each entry ← node.get_entries_range(h_min, h_max) do
h ← entry.get_h();
if (h | h_min) & h_max == h then // evaluates to 'true' if quadrant and query overlap.
[ ... ]
end if
repeat
return
The resulting time complexity is compared to the of the full iteration.[4]
Traverse quadrants that overlap with query box
[edit]For higher dimensions with larger nodes it is also possible to avoid iterating through all and instead directly calculate the next higher that overlaps with the query box. The first step puts ``-bits into a given for all quadrants that have no overlap with the query box. The second step increments the adapted and the added ``-bits trigger an overflow so that the non-overlapping quadrants are skipped. The last step removes all the undesirable bits used for triggering the overflow. The logic is described in detail in.[4] The calculation works as follows:
function increment_h(h_input, h_min, h_max) is
h_out = h_input | (~ h_max ) // pre - mask
h_out += 1 // increment
h_out = ( h_out & h_max ) | h_min // post - mask
return h_out
Again, for this can be done on most CPUs in . The resulting time complexity for traversing a node is .[4] This works best if most of the quadrants that overlap with the query box are occupied with an entry.
k-nearest neighbors
[edit]k nearest neighbor searches can be implemented using standard algorithms.[5]
Floating point keys
[edit]The PH-tree can only store integer values. Floating point values can trivially be stored as integers casting them as an integer. However, the authors also propose an approach without loss of precision.[1][4]
Lossless conversion
[edit]Lossless converting of a floating point value into an integer value (and back) without loss if precision can be achieved by simply interpreting the 32 or 64 bits of the floating point value as an integer (with 32 or 64 bits). Due to the way that IEEE 754 encodes floating point values, the resulting integer values have the same ordering as the original floating point values, at least for positive values. Ordering for negative values can be achieved by inverting the non-sign bits.[1][4]
Example implementations in Java:
long encode(double value) {
long r = Double.doubleToRawLongBits(value);
return (r >= 0) ? r : r ^ 0x7FFFFFFFFFFFFFFFL;
}
Example implementations in C++:
std::int64_t encode(double value) {
std::int64_t r;
memcpy(&r, &value, sizeof(r));
return r >= 0 ? r : r ^ 0x7FFFFFFFFFFFFFFFL;
}
Encoding (and the inverse decoding) is lossless for all floating point values. The ordering works well in practice, including and . However, the integer representation also turns into a normal comparable value (smaller than infinity), infinities are comparable to each other and is larger than .[6] That means that, for example, a query range will not match a value of . In order to match the query range needs to be .[citation needed]
Hyperbox keys
[edit]In order to store volumes (axis-aligned hyper-boxes) as keys, implementations typically use corner representation[7] which converts the two -dimensional minimum and maximum corners of a box into a single key with dimensions, for example by interleaving them: .
This works trivially for lookup, insert and remove operations. Window queries need to be converted from -dimensional vectors to -dimensional vectors. For example, for a window query that matches all boxes that are completely inside the query box, the query keys are:[7][8]
For a window query operation that matches all boxes that intersect with a query box, the query keys are:[8]
Scalability
[edit]In high dimensions with less than entries, a PH-tree may have only a single node, effectively “degenerating” into a B-Tree with Z-order curve. The add/remove/lookup operations remain and window queries can use the quadrant filters. However, this cannot avoid the curse of dimensionality, for high dimensional data with or a PH-tree is only marginally better than a full scan.[9]
Uses
[edit]Research has reported fast add/remove/exact-match operations with large and fast changing datasets.[10] Window queries have been shown to work well especially for small windows[11] or large dataset[12]
The PH-tree is mainly suited for in-memory use.[10][13][14] The size of the nodes (number of entries) is fixed while persistent storage tends to benefit from indexes with configurable node size to align node size with page size on disk. This is easier with other spatial indexes, such as R-Trees.
Implementations
[edit]- Java: GitHub repository by original inventor
- C++: GitHub repository by original inventor
- C++: GitHub repository
- C++: GitHub repository
See also
[edit]External links
[edit]References
[edit]- ^ a b c d e f g h i j k l m n o p Zäschke, Tilmann; Zimmerli, Christoph; Norrie, Moira C. (June 2014). "The PH-tree". Proceedings of the 2014 ACM SIGMOD International Conference on Management of Data. pp. 397–408. doi:10.1145/2588555.2588564. ISBN 9781450323765. S2CID 6862850. Retrieved 10 February 2022.
- ^ Kouahla, Z.; Benrazek, A.-E.; Ferrag, M. A.; Farou, B.; Seridi, H.; Kurulay, M.; Anjum, A.; Asheralieva, A. (2022). "Survey on Big IoT Data Indexing: Potential Solutions, Recent Advancements, and Open Issues". Future Internet. 14 (1): 19. doi:10.3390/fi14010019.
- ^ Mahmood, A. R.; Punni, S.; Aref, W. G. (2018). "Spatio-temporal access methods: a survey (2010 – 2017)". Geoinformatica. 23 (1): 1–36. doi:10.1007/s10707-018-0329-2. S2CID 106407322.
- ^ a b c d e f g h i j Zäschke, Tilmann; Norrie, Moira (2017). "Efficient Z-Ordered Traversal of Hypercube Indexes". Datenbanksysteme für Business, Technologie und Web (BTW 2017). Lecture Notes in Informatics. Vol. P-265. Bonn: Gesellschaft für Informatik. pp. 465–484. doi:10.3929/ethz-a-010802003. ISBN 9783885796596.
- ^ Hjaltason, Gísli R.; Samet, Hanan (June 1999). "Distance browsing in spatial databases". ACM Transactions on Database Systems. 24 (2): 265–318. doi:10.1145/320248.320255. S2CID 10881319. Retrieved 12 February 2022.
- ^ IEEE 754 2019
- ^ a b Seeger, B.; Kriegel, H. P. (1988). "Techniques for Design and Implementation of Efficient Spatial Access Methods". Proceedings 1988 VLDB Conference: 14th International Conference on Very Large Data Bases. 14: 360.
- ^ a b Samet, Hanan (2006). Foundations of multidimensional and metric data structures. San Francisco: Elsevier/Morgan-Kaufmann. pp. 440–441, 453–457. ISBN 0-12-369446-9.
- ^ Li, Yan; Ge, Tingjian; Chen, Cindy (2020). "Online Indices for Predictive Top-k Entity and Aggregate Queries on Knowledge Graphs". 2020 IEEE 36th International Conference on Data Engineering (ICDE). pp. 1057–1068. doi:10.1109/ICDE48307.2020.00096. ISBN 978-1-7281-2903-7. S2CID 218907333.
- ^ a b Sprenger, Stefan (2019). Efficient Processing of Range Queries in Main Memory (doctoralThesis). Humboldt-Universität zu Berlin. doi:10.18452/19786.
- ^ Khatibi, A.; Porto, F.; Rittmeyer, J. G.; Ogasawara, E.; Valduriez, P.; Shasha, D. (August 2017). "Pre-processing and Indexing Techniques for Constellation Queries in Big Data". Big Data Analytics and Knowledge Discovery (PDF). Lecture Notes in Computer Science. Vol. 10440. pp. 164–172. doi:10.1007/978-3-319-64283-3_12. ISBN 978-3-319-64282-6. S2CID 3857469.
- ^ Winter, C.; Kipf, A.; Anneser, C.; Zacharatou, E. T.; Neumann, T.; Kemper, A. (2020). "Database Technology". GeoBlocks: A Query-Cache Accelerated Data Structure for Spatial Aggregation over Polygons. Vol. 23. OpenProceedings.org. pp. 169–180. doi:10.5441/002/edbt.2021.16.
- ^ Wang, S.; Maier, D.; Ooi, B. (2016). "Fast and Adaptive Indexing of Multi-Dimensional Observational Data". Proceedings of the VLDB Endowment. 9 (14): 1683. doi:10.14778/3007328.3007334.
- ^ Herrera, Stiw; da Silva, Larissa Miguez; Reis, Paulo Ricardo; Silva, Anderson; Porto, Fabio (2021). "Managing Sparse Spatio-Temporal Data in SAVIME: an Evaluation of the PH-tree Index". Anais do XXXVI Simpósio Brasileiro de Bancos de Dados: 337–342. doi:10.5753/sbbd.2021.17895. S2CID 245185935.



















































![{\displaystyle [0.0,10.0]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/880a44e4b1f9dbc5fb6cac059accc1ac08c70a45)
![{\displaystyle [-0.0,10.0]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7c40e10f40dbff2195aa590a1630003752ec1aff)








