Period-doubling bifurcation
In dynamical systems theory, a period-doubling bifurcation occurs when a slight change in a system's parameters causes a new periodic trajectory to emerge from an existing periodic trajectory—the new one having double the period of the original. With the doubled period, it takes twice as long (or, in a discrete dynamical system, twice as many iterations) for the numerical values visited by the system to repeat themselves.
A period-halving bifurcation occurs when a system switches to a new behavior with half the period of the original system.
A period-doubling cascade is an infinite sequence of period-doubling bifurcations. Such cascades are a common route by which dynamical systems develop chaos.[1] In hydrodynamics, they are one of the possible routes to turbulence.[2]

Examples
[edit]
Logistic map
[edit]The logistic map is
where is a function of the (discrete) time .[3] The parameter is assumed to lie in the interval , in which case is bounded on .
For between 1 and 3, converges to the stable fixed point . Then, for between 3 and 3.44949, converges to a permanent oscillation between two values and that depend on . As grows larger, oscillations between 4 values, then 8, 16, 32, etc. appear. These period doublings culminate at , beyond which more complex regimes appear. As increases, there are some intervals where most starting values will converge to one or a small number of stable oscillations, such as near .
In the interval where the period is for some positive integer , not all the points actually have period . These are single points, rather than intervals. These points are said to be in unstable orbits, since nearby points do not approach the same orbit as them.
Quadratic map
[edit]Real version of complex quadratic map is related with real slice of the Mandelbrot set.
-
Period-doubling cascade in an exponential mapping of the Mandelbrot set
-
1D version with an exponential mapping
-
period doubling bifurcation
Kuramoto–Sivashinsky equation
[edit]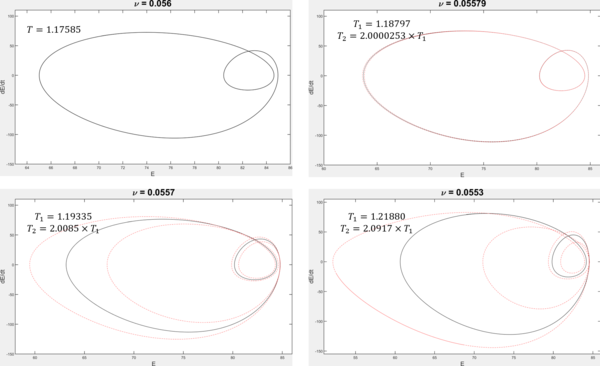
The Kuramoto–Sivashinsky equation is an example of a spatiotemporally continuous dynamical system that exhibits period doubling. It is one of the most well-studied nonlinear partial differential equations, originally introduced as a model of flame front propagation.[4]
The one-dimensional Kuramoto–Sivashinsky equation is
A common choice for boundary conditions is spatial periodicity: .
For large values of , evolves toward steady (time-independent) solutions or simple periodic orbits. As is decreased, the dynamics eventually develops chaos. The transition from order to chaos occurs via a cascade of period-doubling bifurcations,[5][6] one of which is illustrated in the figure.
Logistic map for a modified Phillips curve
[edit]Consider the following logistical map for a modified Phillips curve:
where :
- is the actual inflation
- is the expected inflation,
- u is the level of unemployment,
- is the money supply growth rate.
Keeping and varying , the system undergoes period-doubling bifurcations and ultimately becomes chaotic.[citation needed]
Experimental observation
[edit]Period doubling has been observed in a number of experimental systems.[7] There is also experimental evidence of period-doubling cascades. For example, sequences of 4 period doublings have been observed in the dynamics of convection rolls in water and mercury.[8][9] Similarly, 4-5 doublings have been observed in certain nonlinear electronic circuits.[10][11][12] However, the experimental precision required to detect the ith doubling event in a cascade increases exponentially with i, making it difficult to observe more than 5 doubling events in a cascade.[13]
See also
[edit]- List of chaotic maps
- Complex quadratic map
- Feigenbaum constants
- Universality (dynamical systems)
- Sharkovskii's theorem
Notes
[edit]- ^ Alligood (1996) et al., p. 532
- ^ Thorne, Kip S.; Blandford, Roger D. (2017). Modern Classical Physics: Optics, Fluids, Plasmas, Elasticity, Relativity, and Statistical Physics. Princeton University Press. pp. 825–834. ISBN 9780691159027.
- ^ Strogatz (2015), pp. 360–373
- ^ Kalogirou, A.; Keaveny, E. E.; Papageorgiou, D. T. (2015). "An in-depth numerical study of the two-dimensional Kuramoto–Sivashinsky equation". Proceedings of the Royal Society A: Mathematical, Physical and Engineering Sciences. 471 (2179): 20140932. Bibcode:2015RSPSA.47140932K. doi:10.1098/rspa.2014.0932. ISSN 1364-5021. PMC 4528647. PMID 26345218.
- ^ Smyrlis, Y. S.; Papageorgiou, D. T. (1991). "Predicting chaos for infinite dimensional dynamical systems: the Kuramoto-Sivashinsky equation, a case study". Proceedings of the National Academy of Sciences. 88 (24): 11129–11132. Bibcode:1991PNAS...8811129S. doi:10.1073/pnas.88.24.11129. ISSN 0027-8424. PMC 53087. PMID 11607246.
- ^ Papageorgiou, D.T.; Smyrlis, Y.S. (1991), "The route to chaos for the Kuramoto-Sivashinsky equation", Theoretical and Computational Fluid Dynamics, 3 (1): 15–42, Bibcode:1991ThCFD...3...15P, doi:10.1007/BF00271514, hdl:2060/19910004329, ISSN 1432-2250, S2CID 116955014
- ^ see Strogatz (2015) for a review
- ^ Giglio, Marzio; Musazzi, Sergio; Perini, Umberto (1981). "Transition to Chaotic Behavior via a Reproducible Sequence of Period-Doubling Bifurcations". Physical Review Letters. 47 (4): 243–246. Bibcode:1981PhRvL..47..243G. doi:10.1103/PhysRevLett.47.243. ISSN 0031-9007.
- ^ Libchaber, A.; Laroche, C.; Fauve, S. (1982). "Period doubling cascade in mercury, a quantitative measurement" (PDF). Journal de Physique Lettres. 43 (7): 211–216. doi:10.1051/jphyslet:01982004307021100. ISSN 0302-072X.
- ^ Linsay, Paul S. (1981). "Period Doubling and Chaotic Behavior in a Driven Anharmonic Oscillator". Physical Review Letters. 47 (19): 1349–1352. Bibcode:1981PhRvL..47.1349L. doi:10.1103/PhysRevLett.47.1349. ISSN 0031-9007.
- ^ Testa, James; Pérez, José; Jeffries, Carson (1982). "Evidence for Universal Chaotic Behavior of a Driven Nonlinear Oscillator". Physical Review Letters. 48 (11): 714–717. Bibcode:1982PhRvL..48..714T. doi:10.1103/PhysRevLett.48.714. ISSN 0031-9007.
- ^ Arecchi, F. T.; Lisi, F. (1982). "Hopping Mechanism Generating1fNoise in Nonlinear Systems". Physical Review Letters. 49 (2): 94–98. Bibcode:1982PhRvL..49...94A. doi:10.1103/PhysRevLett.49.94. ISSN 0031-9007.
- ^ Strogatz (2015), pp. 360–373
References
[edit]- Alligood, Kathleen T.; Sauer, Tim; Yorke, James (1996). Chaos: An Introduction to Dynamical Systems. Textbooks in Mathematical Sciences. Springer-Verlag New York. doi:10.1007/0-387-22492-0_3. ISBN 978-0-387-94677-1. ISSN 1431-9381.
- Giglio, Marzio; Musazzi, Sergio; Perini, Umberto (1981). "Transition to Chaotic Behavior via a Reproducible Sequence of Period-Doubling Bifurcations". Physical Review Letters. 47 (4): 243–246. Bibcode:1981PhRvL..47..243G. doi:10.1103/PhysRevLett.47.243. ISSN 0031-9007.
- Kalogirou, A.; Keaveny, E. E.; Papageorgiou, D. T. (2015). "An in-depth numerical study of the two-dimensional Kuramoto–Sivashinsky equation". Proceedings of the Royal Society A: Mathematical, Physical and Engineering Sciences. 471 (2179): 20140932. Bibcode:2015RSPSA.47140932K. doi:10.1098/rspa.2014.0932. ISSN 1364-5021. PMC 4528647. PMID 26345218.
- Kuznetsov, Yuri A. (2004). Elements of Applied Bifurcation Theory. Applied Mathematical Sciences. Vol. 112 (3rd ed.). Springer-Verlag. ISBN 0-387-21906-4. Zbl 1082.37002.
- Libchaber, A.; Laroche, C.; Fauve, S. (1982). "Period doubling cascade in mercury, a quantitative measurement" (PDF). Journal de Physique Lettres. 43 (7): 211–216. doi:10.1051/jphyslet:01982004307021100. ISSN 0302-072X.
- Papageorgiou, D.T.; Smyrlis, Y.S. (1991), "The route to chaos for the Kuramoto-Sivashinsky equation", Theoret. Comput. Fluid Dynamics, 3 (1): 15–42, Bibcode:1991ThCFD...3...15P, doi:10.1007/BF00271514, hdl:2060/19910004329, ISSN 1432-2250, S2CID 116955014
- Smyrlis, Y. S.; Papageorgiou, D. T. (1991). "Predicting chaos for infinite dimensional dynamical systems: the Kuramoto-Sivashinsky equation, a case study". Proceedings of the National Academy of Sciences. 88 (24): 11129–11132. Bibcode:1991PNAS...8811129S. doi:10.1073/pnas.88.24.11129. ISSN 0027-8424. PMC 53087. PMID 11607246.
- Strogatz, Steven (2015). Nonlinear Dynamics and Chaos: With applications to Physics, Biology, Chemistry and Engineering (2nd ed.). CRC Press. ISBN 978-0813349107.
- Cheung, P. Y.; Wong, A. Y. (1987). "Chaotic behavior and period doubling in plasmas". Physical Review Letters. 59 (5): 551–554. Bibcode:1987PhRvL..59..551C. doi:10.1103/PhysRevLett.59.551. ISSN 0031-9007. PMID 10035803.







![{\displaystyle [0,4]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/74e35bf9a1852b3714b44393625cf4c127c946a7)
![{\displaystyle [0,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/738f7d23bb2d9642bab520020873cccbef49768d)



















